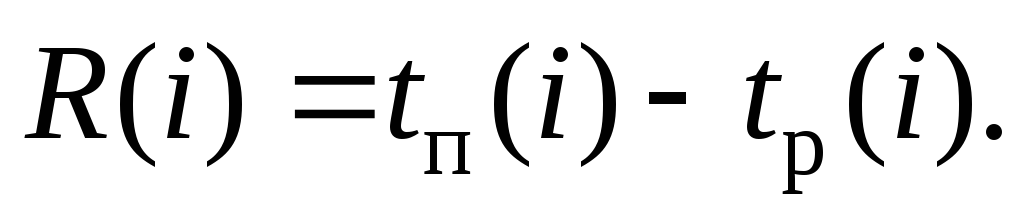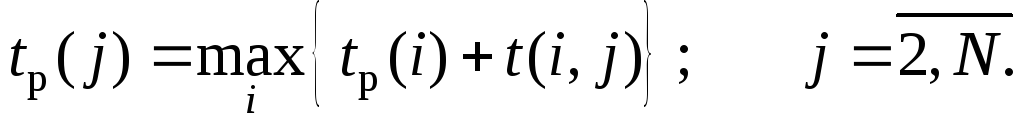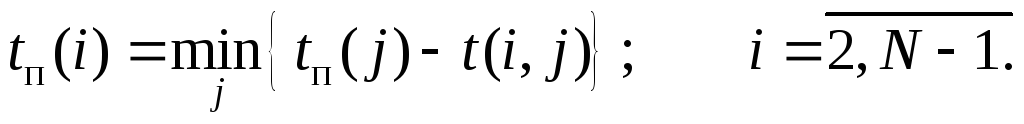Оптимизация сетевой модели по критерию время – число исполнителей
После построения сетевого графика и определения его временных параметров проводят проверку соответствия полученных сроков продолжительности разработки нормативным или директивным срокам. Далее анализируют структуру сетевой модели, выявляя неоднородность напряженности работ проекта.
В настоящее время на практике сетевую модель вначале корректируют по времени, т. е. приводят ее к заданному сроку окончания проекта. Затем приступают к корректировке графика по критерию распределения ресурсов, начиная с трудовых ресурсов.
Минимизация числа исполнителей проекта при сохранении времени его выполнения
- минимизировать количество одновременно занятых исполнителей;
- выровнять потребность в трудовых ресурсах на протяжении всего срока выполнения проекта.
- перемещение работ по оси времени возможно осуществлять только вправо (откладывая их начало);
- работы критического пути трогать нельзя, т. к. это приведет к увеличению срока выполнения всего проекта;
- работы, имеющие свободный резерв времени, можно спокойно перемещать на величину этого резерва;
- перемещение работ, имеющих только полный резерв времени, требует аналогичного сдвига последующих работ;
- передвигаемые работы на линейной диаграмме выделяют, отмечая заметным символом: звездочкой, штрихом, цветом и т.п.
Рис. 1. Пример сетевого графика
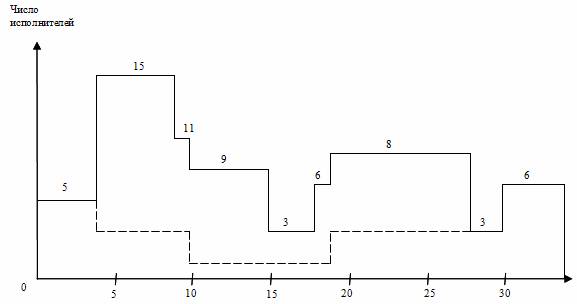
Проведем более детальный анализ линейной диаграммы и карты проекта с целью оптимизации трудовых ресурсов: выравнивая потребность в них на протяжении всего проекта и минимизируя количество одновременно занятых исполнителей. График ежедневной потребности ресурса показывает, что минимальное число исполнителей не может быть меньше 6 человек, что определяется их потребностью для работ критического пути. А 15 исполнителей на участке 5-10 дни проекта является явно завышенным и подлежит коррекции в первую очередь.
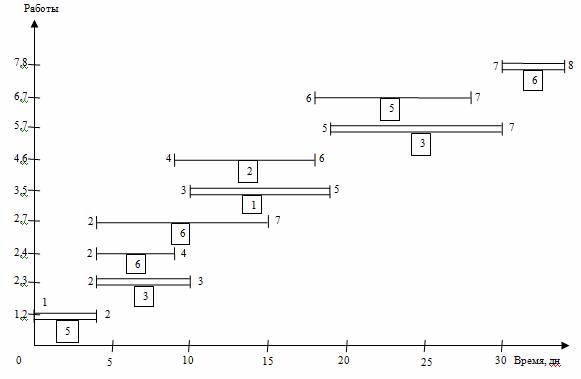
Рис. 2. Линейная диаграмма и карта проекта до оптимизации
15 исполнителей заняты на работах 2,3; 2,4 и 2,7. Работу 2,3 трогать нельзя, т. к. это работа критического пути. Работа 2,4 имеет только полный резерв, но не имеет свободного резерва времени. Работа 2,7 имеет солидный свободный резерв времени и поэтому наиболее предпочтительна для оптимизации. Используем часть свободного резерва, переместив работу 2,7 (5-15 дни) на 5 дней (ее новый срок 10-20 дни). Тем самым максимально необходимое число исполнителей уменьшилось до 9 человек, т.е. задачу минимизации трудовых ресурсов проекта можно принять завершенной.
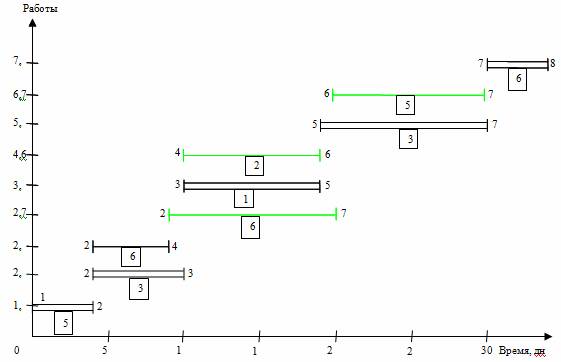
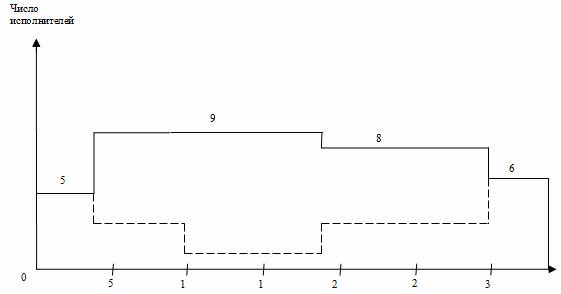
Рис. 3. Линейная диаграмма и карта проекта после оптимизации
Далее решим задачу выравнивания потребности в ресурсах, анализируя интервалы времени, связанные с «провалами» карты проекта. С учетом перемещения работы 2,7 падения спроса на исполнителей в середине проекта (16-18 дни) уже не будет, но он останется ближе к концу проекта (29-30 дни). Чтобы сгладить график загрузки, переместим работу 6,7 (19-28 дни), имеющую свободный резерв времени, на 2 дня (новый срок 21-30 дни). Также для целей выравнивания потребности в трудовых ресурсах переместим работу 4,6 (10-18 дни) на 1 день (11-19 дни).
В итоге оптимизации приходим к линейной диаграмме и карте проекта, представленными на рис. 3. Из графика видно улучшение равномерности загрузки исполнителей: новая ежедневная потребность ресурса составляет от 5 до 9 человек в зависимости от этапа выполнения проекта, резких колебаний занятости нет. Длительность выполнения всего проекта при этом осталась неизменной (34 дня), т. е. необходимое условие оптимизации соблюдено. Видеоинструкция
8.3. Анализ сетевой модели
Основные параметры сетевой модели. К основным параметрам СМ относятся резервы времени. Резерв временисобытия – промежуток времени, на который может быть отсрочено наступление этого события без нарушения сроков завершения разработки в целом.
Все события, за исключением событий, принадлежащих критическому пути, имеют резерв R(i), который определяется как разность между поздним и ранним сроками наступления события:
(8.3.1)
Ранний срок наступления события tр – это минимальный срок, необходимый для выполнения всех работ, предшествующих данному событию. Это время находится путем выбора максимального значения из продолжительности всех путей, ведущих к данному событию, причемtр(1) = 0, а tр(N) = tкр(L):
(8.3.2)
Поздний срок наступления события tп характеризует самый поздний допустимый срок, к которому должно совершиться событие, не вызывая при этом срыва срока свершения конечного события.
(8.3.3)
Этот показатель определяется «обратным ходом», начиная с завершающего события, с учетом соотношения tп(N) = tр(N).
Для всех работ (i,j) на основе ранних и поздних сроков свершения событий, можно определить следующие показатели:
(8.3.4)
Полный резерв временипоказывает, на сколько можно увеличить время выполнения конкретной работы при условии, что срок выполнения всего комплекса работ не изменится.
Независимый резерв времени соответствует случаю, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие – начинаются в ранние сроки. Использование этого резерва не влияет на величину резервов времени других работ.
Путь характеризуется двумя показателями – продолжительностью и резервом. Продолжительность пути определяется суммой продолжительностей составляющих его работ. Резерв определяется как разность между длинами критического и рассматриваемого путей. Из этого определения следует, что работы, лежащие на критическом пути и сам критический путь имеют нулевой резерв времени. Резерв времени пути показывает, на сколько может увеличиться продолжительность работ, составляющих данный путь, без изменения продолжительности общего срока выполнения всех работ.
Перечисленные выше показатели и характеристики СМ могут быть получены на основе приведенных аналитических формул, а процесс вычислений отображен непосредственно на графике, либо в матрице (размерности ), либо в таблице.
Таблица параметров сетевого графика. Рассмотрим табличный способ расчета основных показателей СМ, которая представлена на рис.39. Результаты расчетов приведены в табл.9.
В первом и втором столбце таблицы последовательно записан перечень работ (i,j) и их продолжительность. Здесьi –начальное событие, аj – конечное событие пути (i,j). Заполнение таблицы начинается с расчета раннего срока начала работtрн(i,j) в столбце 3. Для начальных работ (i= 1) в столбце 3 записываются нули, а в остальные строки столбца 3 записываются максимальные значения предшествующих работ (см формулы (8.3.4), (8.3.2)).
значения в столбце 4 получается в результате суммирования значений в столбцах 2 и 3. Например,tро (2,4) = 3+6 = 9.
Столбцы 6 и 5 заполняются «обратным ходом», т.е. снизу вверх. Для этого просматриваются строки, оканчивающиеся на номер последнего события
(j = N), и из столбца 4 выбирается максимальная величина, которая записывается в столбец 6 по всем строчкам, оканчивающимся на номер последнего события (tпо (i,N)). В нашем примереtпо (i,N) = 33.
Для расчета tпо (i,j) в столбце 6 используются формулы (8.3.4) и (8.3.3). Затем для этих строк находится содержимое столбца 5, как разность между столбцами 6 и 2 (см. формулы (8.3.4)). Например, получим tпн (10,11) = 33 – 9 = 24.
Далее просматриваются строки, расположенные выше (j = N–1,N–2 и т.д.). Процесс повторяется до тех пор, пока не будут заполнены все строки по столбцам 6 и 5.
Содержимое столбца 7 равно разности соответствующих строк столбцов 5 и 3 или столбцов 6 и 4 (см. формулу (8.3.1)). Столбец 8 получается по формуле из (8.3.4).