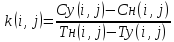8.3. Оптимизация сетевых моделей
8.3.1. Оптимизация использования ресурса рабочей силы
При оптимизации использования ресурса рабочей силы сетевые работы чаще всего стремятся организовать таким образом, чтобы:
− количество одновременно занятых исполнителей было минимальным;
− выровнять потребность в людских ресурсах на протяжении срока выполнения проекта.
Для проведения подобных видов оптимизации необходим график загрузки.
На графике загрузки по горизонтальной оси откладывается время, например в днях, по вертикальной – количество человек, занятых работой в каждый конкретный день. Для построения графика загрузки необходимо:
− на графике привязки над каждой работой написать количество ее исполнителей;
− подсчитать количество работающих в каждый день исполнителей и отложить на графике загрузки.
Для удобства построения и анализа, графики загрузки и привязки следует располагать один над другим.
Пример построения графика загрузки. Описанные виды оптимизации могут быть выполнены с помощью сдвига работ, который осуществляется за счет резервов времени: свободного или полного. После сдвига работы, работники выполняют ее уже в другие дни, и поэтому для каждого дня изменяется количество исполнителей занятых одновременно.
Резервы работ можно определить без специальных расчетов, только с помощью графика привязки.
Различие в использовании свободных и полных резервов заключается в том, что при сдвиге работы, с использованием свободного резерва, моменты начала следующих за ней работ остаются неизменными (т.е. последующие работы не сдвигаются). При сдвиге работы, с использованием полного резерва, все последующие работы сдвигаются.
8.3.2. Оптимизация типа «время – затраты»
Целью оптимизации по критерию «время – затраты» является сокращение времени выполнения проекта в целом. Эта оптимизация имеет смысл только в том случае, когда длительность выполнения работ может быть уменьшена за счет задействования дополнительных ресурсов, что влечет повышение затрат на выполнение работ. Для оценки величины дополнительных затрат, связанных с ускорением выполнения той или иной работы, используются либо нормативы, либо данные о выполнении аналогичных работ в прошлом.
Исходными данными для проведения оптимизации являются:
− Tн(i,j) – нормальная длительность работы;
− Tу(i,j) – ускоренная длительность;
− Cн(i,j) – затраты на выполнение работы в нормальный срок;
− Cу(i,j) – затраты на выполнение работы в ускоренный срок.
Т.о. каждая работа имеет некоторый максимальный запас времени для сокращения своей длительности Zmax(i,j) =Tн(i,j) −Tу(i,j).
Для анализа сетевой модели в данном виде оптимизации используется коэффициент нарастания затрат (коэффициент ускорения)
который имеет смысл (Дополнительный вопрос: какой смысл?) затрат денежных средств для сокращения длительности выполнения работы (i,j) на один день.
Оптимизация критического пути. Оптимизация критического пути заключается в улучшении его в соответствии с принятым критерием.
В принципе, этими критериями могут быть: время, стоимость, людские и материальные ресурсы и др.
В настоящее время оптимизация сетевых графиков выполняется в основном только по критерию времени.
Оптимизация может производиться с различными целями:
1. если критический путь со временем T превышает заданные сроки T 0, то оптимизация по времени заключается в сокращении критического пути.
Для сокращения критического пути, естественно, имеет смысл форсировать критические работы. Их можно ускорить, например:
1. за счёт дополнительных сил и средств;
2. за счёт переброски сил и средств с некритических работ на критические.
Если используется пункт 1, то возникает типичная задача исследования операций: какие дополнительные средства x 1, x 2 . x n и в какие критические работы нужно вложить, чтобы критический путь T ≤ T 0, а расход дополнительных средств был минимальным.
Если используется пункт 2, т.е. для оптимизации критического пути перебрасываются имеющиеся средства с некритических работ на критические.
Общая схема проведения оптимизации:
1. проводится расчет сети исходя из нормальных длительностей работ;
2. определяется сумма затрат на выполнение всего проекта при нормальной продолжительности работ;
3. рассматривается возможность сокращения продолжительности проекта.
Поскольку этого можно достичь за счет уменьшения продолжительности какой-либо критической работы, то только такие операции подвергаются анализу;
3.1. для сокращения выбирается критическая работа с min коэффициентом нарастания затрат k(i,j), у которой есть запас сокращения времени;
3.2. определяется время Δt(i,j), на которое необходимо сжать длительность работы (i,j). При этом руководствуются следующими соображениями;
3.2.1. максимально возможный запас времени для сокращения работы на текущий момент Z(i,j) ограничивается значением Tу(i,j), т.е.
Z(i,j)=tт(i,j)−Tу(i,j), где tт (i,j) — текущее время выполнения работы
(tт(i,j) =Tн(i,j) только для работ еще не подвергшихся сокращению);
3.2.2. кроме критического пути длительностью Tкр в сети есть подкритический путь длительностью Tп . Критический путь нельзя сократить больше, чем ΔT=Tкр−Tп, поскольку в этом случае критический путь перестанет быть таковым, а подкритический путь наоборот станет критическим;
3.2.3. исходя из вышесказанного, время сокращения длительности выбранной работы (i,j) равно Δt=tт (i,j)−min[Z(i,j),ΔT]. Другими словами, если разность между длительностью критического и подкритического путей ΔT меньше текущего запаса времени сокращения работы Z(i,j), то имеет смысл сокращать работу только на ΔT дней. В противном случае можно сокращать работу полностью на величину Z(i,j);
4. в результате сжатия критической операции получают новый календарный план, возможно с новыми критическими и подкритическими путями, и обязательно с новыми более высокими затратами на выполнение проекта. Это происходит вследствие удорожания ускоренной работы. Общая стоимость проекта увеличивается на ΔC = k(i, j)Δt;
5. переход на шаг 3, который повторяется до тех пор, пока стоимость проекта уменьшается.
В результате оптимизации строится график «Время – затраты».
Под параметрами работ Cн(i,j) и Cу(i,j) понимаются так называемые прямые затраты, т.е. косвенные затраты типа административно-управленческих во внимание не принимаются. Однако их влияние учитывается при выборе окончательного календарного плана проекта. В отличие от прямых затрат косвенные затраты при уменьшении продолжительности проекта убывают, что показано на графике. Оптимальный календарный план соответствует минимуму общих затрат (точка А).
8.3.3. Неопределенность времени выполнения операций
В описанных методах анализа сетей предполагалось, что время выполнения работ точно известно, однако на практике сроки выполнения работ обычно довольно неопределенны. В таких случаях обычно используют экспертные оценки минимальной (a), максимальной (b) и наиболее вероятной длительности (m) работ для расчета их ожидаемой продолжительности.
Данный метод основан на предположении, что время выполнения каждой отдельной работы аппроксимируется β – распределением. При таком подходе можно оценивать вероятности наступления событий в пределах их ранних и поздних сроков, вероятность завершения проекта к заранее установленной дате и другие вероятностные характеристики.
Анализ и оптимизация сетевой модели
Первоначально разработанная сетевая модель обычно не является лучшей по срокам выполнения работ и использования ресурсов. Поэтому исходная сетевая модель подвергается анализу и оптимизации по одному из ее параметров.
Анализ позволяет оценить целесообразность структуры модели, определить степень сложности выполнения каждой работы, загрузку исполнителей работ на всех этапах выполнения комплекса работ.
Относительная сложность соблюдения сроков выполнения работ на некритических путях характеризуется коэффициентом напряженности работ :
где — продолжительность максимального пути, проходящего через данную работу;
— продолжительность отрезка этого пути, совпадающего с критическим путем;
— продолжительность критического пути.
Чем больше коэффициент напряженности, тем сложнее выполнить работы в установленные сроки.
Используя понятие «резерва времени пути», можно определить следующим образом:
При этом необходимо иметь в виду, что резерв времени R(Li) пути Li может быть распределен между отдельными работами, находящимися на указанном пути, только в пределах зависимых резервов времени этих работ.
Величина коэффициента напряженности у разных работ в сети лежит в пределах 0
Для всех работ критического пути равен единице. Величина коэффициента напряженности помогает при установлении плановых сроков выполнения работ оценить, насколько свободно можно располагать имеющимися резервами времени. Этот коэффициент дает исполнителям работ представление о степени срочности работ и позволяет определить очередность их выполнения, если они не определяются технологическими связями работ.
Для анализа сетевой модели используется коэффициент свободы (i,j), который показывает степень свободы или независимости циклов работ, имеющих свободный резерв времени, а также показывает, во сколько раз можно увеличить длительность работы t(i, j), не влияя на сроки свершения всех событий и остальных работ сети:
При этом (i, j)>1 всегда. Если (i, j)1, то это указывает на отсутствие независимого резервного времени у работы (i,j).
Оптимизация сетевых моделей по одному из ее параметров может быть осуществлена графическим или аналитическим методом. Решая задачу оптимизации сетевой модели, обычно рассчитывают минимальную продолжительность выполнения комплекса работ при ограничениях на используемые ресурсы.
Оптимизация сетевой модели, осуществляемая аналитическим методом, заключается в том, что в ее основу положена та закономерность, при которой время выполнения любой работы (t) прямо пропорционально ее объему (Q) и обратно пропорционально числу исполнителей (m), занятых на данной работе:
Время, необходимое для выполнения всего комплекса работ , определяется как сумма длительностей составляющих работ:
Однако рассчитанное таким образом общее время не будет минимальным, даже если количество исполнителей соответствует трудоемкости этапов.
Минимальное время для комплекса последовательно выполняемых работ и других разновидностей фрагментов сетевых моделей можно найти методом условно-эквивалентной трудоемкости.
Под условно-эквивалентной трудоемкостью понимают такую величину затрат труда, при которой численность исполнителей эквивалентной специальности распределяется между составляющими работами, обеспечивает наименьшее время их исполнения.
Условно-эквивалентная трудоемкость определяется по формуле:
где — трудоемкости предшествующей и последующей работ.
Минимальное время выполнения работ будет обеспечено при следующем распределении работающих по этапам:
где — общее количество работающих на определенных этапах.
Графический метод оптимизации сетевой модели — «время-затраты»
Метод «время-затраты» заключается в установлении оптимального соотношения между продолжительностью и стоимостью работ.
Определение затрат и ресурсов, необходимых для выполнения каждой работы, производится после разработки сетевого графика.
Таким образом, материальные и трудовые ресурсы планируются на основе общей структуры сети, созданной с помощью прогнозирования временных оценок.
Рис. 7. График «время-затраты»
Для построения графиков «время-затраты» (рис. 7) для каждой работы задаются:
— минимально возможные денежные затраты на выполнение работы (при условии выполнения работы за нормальное время );
— минимально возможное время выполнения работы при максимальных денежных затратах .
При определении первой пары оценок упор делается на максимальное сокращение затрат, а при определении второй — на максимальное сокращение времени.
Приближенно определить размеры дополнительных затрат, необходимых для сокращения срока выполнения работы, или решить обратную задачу возможно с помощью графика с аппроксимирующей прямой. Величина дополнительных денежных затрат, необходимых для выполнения работы в сокращенное время , составит
Для каждого вида работ рассчитывается и строится свой график, характеризующийся наклоном аппроксимирующей прямой.
Используя линейную зависимость «затраты-время» для каждого вида работ, можно вычислить коэффициент возрастания затрат на единицу времени:
Экономическая эффективность от внедрения СПУ определяется в первую очередь возможностями уменьшения общего цикла работ и сокращением затрат за счет более рационального использования трудовых, материальных и денежных ресурсов.
Уменьшение длительности комплекса работ обеспечивает сокращение сроков окупаемости инвестиций, более раннему выводу товара на рынок, что способствует конкурентному успеху фирмы.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: