Что определяет критический путь в сетевой модели

8.5 Сети. Критический путь

Часто приходится решать задачи, в которых каждому ребру заданного графа приписано некоторое положительное (неотрицательное) число (его вес). Обычно, граф нагруженный подобным образом, называется сетью, его вершины – узлами, а ребра – дугами.

Предположим, что требуется проанализировать сложный проект с точки зрения минимальных временных затрат на его выполнение. Для этого проект разбивают на отдельные этапы (работы, операции), оценивают время, необходимое на проведение каждой работы. Составляют таблицу, в которую заносят все виды работ по проекту, их продолжительность и последовательность выполнения.

По данным таблицы строится ориентированная сеть, дуги которой соответствуют работам проекта, а узлы – событиям, обозначающим начало и/или конец этапов. Каждая дуга нагружена числом, равным продолжительности выполнения соответствующей работы. Понятно, что операции, соответствующие дугам, исходящим из произвольного узла сети, не могут начаться прежде, чем закончатся операции, отвечающие дугам, входящим в этот узел.

Подобная сеть называется сетевым графиком проекта или диаграммой работ.

В результате вычерчивания диаграммы работ определяется путь, наибольшей продолжительностью. Этот путь называется критическим. Он и определяет минимальное время выполнения проекта. Работы, входящие в критический путь, называются критическими работами.

Рассмотрим пример построения сетевого графика, определения критического пути и критических работ, а также минимального времени выполнения всех работ.

Составлена таблица последовательности работ проекта, в которой также указаны предшествующие работы и записано время выполнения каждой работы. Построить сетевой график данного проекта.

Источник

Определение критического пути

Будем предполагать, что время выполнения каждой работы точно известно. Введем следующие определения.

Путь— последовательность взаимосвязанных работ, ведущая из одной вершины проекта в другую вершину. Например (см. Рисунок 48), и – два различных пути.

Рисунок 48. Различные пути на сетевом графике

Длина пути— суммарная продолжительность выполнения всех работ пути.

Полный путь— это путь от исходного к завершающему событию.

Критический путь— полный путь, суммарная продолжительность выполнения всех работ которого является наибольшей.

Очевидно, что минимальное время, необходимое для выполнения любого проекта равно длине критического пути. Именно на работы, принадлежащие критическому пути, следует обращать особое внимание. Если такая работа будет отложена на некоторое время, то время окончания проекта будет отложено на то же время. Если необходимо сократить время выполнения проекта, то в первую очередь нужно сократить время выполнения хотя бы одной работы на критическом пути.

Для того, чтобы найти критический путь, достаточно перебрать все пути и выбрать тот, или те из них, которые имеют наибольшую суммарную продолжительность выполнения работ. Однако для больших проектов реализация такого подхода связана с вычислительными трудностями. Метод критического пути (метод CPM — Critical Path Method) позволяет получить критический путь намного проще.

Расчет сетевой модели начинают с временных параметров событий, которые вписывают непосредственно в вершины сетевого графика (Рисунок 49):

• –ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i;
• –поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
• –резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения.

Рисунок 49. Параметры событий Ранние сроки наступления событий рассчитываются от исходного (S) к завершающему (F) событию следующим образом:

1. для исходного события S: ;
2. для всех остальных событий i: ,

где максимум берется по всем работам (k,i), входящим в событие i; — длительность работы (k,i) (см. Рисунок 50). Рисунок 50. Ранние сроки наступления событий Поздние сроки наступления событий рассчитываются от завершающего к исходному событию:

1. для завершающего события F: ;
2. для всех остальных событий i: ,

где минимум берется по всем работам (i,j), выходящим из события i; — длительность работы (i,j) (см. Рисунок 51). Рисунок 51. Поздние сроки наступления событий Условия критичности пути:

• необходимое условие: нулевые резервы событий, лежащих на критическом пути ;
• достаточное условие: нулевые полные резервы работ, лежащих на критическом пути .— показывает максимальное время, на которое можно увеличить длительность работы (i,j) или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом.

Пример Рассмотрим пример. Компания разрабатывает строительный проект. Исходные данные по основным операциям проекта представлены в таблице. Нужно построить сетевую модель проекта, определить критические пути и проанализировать, как влияет на ход выполнения проекта задержка работы D на 4 недели.

Работа	Непосредственно предшествующая работа	Длительность, недели
A	—	4
B	—	6
C	A, B	7
D	B	3
E	C	4
F	D	5
G	E,F	3

Сетевой график проекта показан на рисунке ниже (см. Рисунок 52). Рисунок 52. Пример. Сетевой график проекта Согласно необходимому условию два полных пути сетевой модели (см. Рисунок 52) имогут быть критическими. Проверим достаточное условие критичности для работ (1,2) и (1,3) , . Путь , начинающийся с работы (1,3) не является критическим, т.к. поскольку как минимум одна из его работ не является критической. Работа (1,3) имеет ненулевой полный резерв, а значит может быть задержана с выполнением, что недопустимо для критических работ. Таким образом, сетевая модель имеет единственный критический путь длительностью 20 недель. За выполнением работ этого пути необходим особый контроль, т.к. любое увеличение их длительности нарушит срок выполнения проекта в целом. Работа D или (2,5) не является критической, ее полный резерв равен 3-м неделям. Это означает, что при задержке работы в пределах 3-х недель срок выполнения проекта не будет нарушен. Поэтому если согласно условию работа D задержится на 4 недели, то весь проект закончится на 1 неделю позже.

Источник

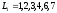
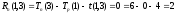
Критический путь

Критический путь (англ. Critical Path Method — СРМ) является основным методом управления проектами, наравне с системой оценки и пересмотра планов проектов и программ (англ. Program Evaluation and Review Technique – PERT). В советской практике оба метода, а также их более сложные модификации объединяются понятием «методы сетевого планирования и управления«.

Критический путь сетевой модели – это самая длинная по срокам последовательная цепочка работ. Как в методе критического пути, так и в методе PERT проекты рассматриваются как сети отдельных событий и работ. Работа в этих системах представляет собой любой элемент проекта, на выполнение которого требуется время, и который может задержать начало выполнения других работ.

Основное различие между методом критического пути и методом PERT заключается в различном подходе к длительности операций. Метод критического пути исходит из того, что длительность операций можно оценить с достаточно высокой степенью точности и определенности.

Метод PERT допускает неопределенность продолжительности операций и анализирует влияние этой неопределенности на продолжительность работ по проекту в целом. Большее распространение получил метод критического пути, а не метод оценки и пересмотра планов. Системы управления работами по реализации проектов, в основе которых лежит метод критического пути, в настоящее время применяются во всем мире.

Планирование работ по методу критического пути

Применение метода критического пути для разработки календарного графика реализации работ по проекту предусматривает в основном выполнение четырех этапов анализа. Их может быть намного больше, если проект более масштабный. В качестве примера для анализа возьмем пример проекта по строительству гаража.

1 этап планирования по методу критического пути

Цели и ограничения

Чтобы установить цели и ограничения в рамках планирования по методу критического пути, необходимо рассмотреть проект в следующих аспектах:

• продолжительность;
• стоимость;
• качество;
• наличие производственных ресурсов (рабочая сила и оборудование);
• другие важные аспекты.

В нашем примере строительства гаража целью будет являться скорейшее завершение строительства при следующих ограничениях:

• Стоимость проекта не должна превышать 150 тыс. руб.
• Обязательное соблюдение технических условий проекта и всех строительных норм.
• Для строительства гаража имеется только двое рабочих.
• Некоторые виды работ нельзя выполнять в ненастную работу.

2 этап планирования по методу критического пути

Продолжительность работ

Второй этап планирования по методу критического пути представляет собой определение работ, входящий в проект, и расчете длительности каждой работы. В нашем примере ожидание того, пока бетонная плита затвердеет, считается операцией, поскольку на это требуется время и начать выполнение других работ до затвердения плиты невозможно. Перечень работ по строительству гаража и их продолжительность показаны на рисунке 1.

3 этап планирования по методу критического пути

Сетевой график работ

Третий этап планирования по методу критического пути включает в себя анализ установки очередности работ и составление графика, отражающего последовательность работ. Некоторые работы должны производиться в определенной последовательности, некоторые можно выполнять параллельно. Очередность работ в основном определяется техническими причинами.

Например, технически невозможно уложить кровлю крыши до тех пор, пока не будет произведена ее обшивка. Но в некоторых случаях очередность определяется по принципу предпочтительности с учетом качества, эффективности или требованиями техники безопасности. Например, электрическую проводку в гараже можно установить сразу после возведения каркаса, но чтобы избежать попадания дождя на арматуру, лучше подождать с электропроводкой до установки боковых стен и крыши. В нашем примере очередность работ выглядит следующим образом:

4 этап планирования по методу критического пути

Линейная диаграмма Ганта и сетевой график

Четвертый этап планирования по методу критического пути предусматривает построение диаграммы Ганта и календарного сетевого графика на основе оценок продолжительности работ (рисунок 1) и полученной сети расписания (рисунок 2). Линейная диаграмма Ганта и сетевого график на данном рисунке построены в программе Microsoft Project по данным проекта по строительству гаража.

Критический путь

Критический путь в проекте — это самая продолжительная последовательная цепочка операций. Критическим путем на диаграмме Ганта, является непрерывная последовательность работ, проходящая через центр графика (Рисунок 2).

Длина критического пути определяет продолжительность работ по выполнению проекта. Любые задержки на критическом пути ведут к увеличению сроков работ. Кроме того, необходимо подчеркнуть, что для сокращения продолжительности работ по проекту необходимо сокращать длину критического пути. Резерв или запас времени – это разность между самым ранним возможным сроком завершения работы и самым поздним допустимым временем ее выполнения.

Резерв времени имеется только в тех работах, которые не лежат на критическом пути, и дает некоторую степень гибкости при календарном планировании таких работ. Линейная диаграмма Ганта и сетевой график дают наглядную и понятную картину последовательности работ по реализации проекта помимо того, что такие графики показывают начало и окончание работы. Они четко указывают на очередность выполнения работ. На линейной диаграмме Ганта и сетевом графике наглядно видны последствия запаздывания любой работы с точки зрения времени реализации всего проекта.

Алексей Голубицкий, компания Alawar

Источник