Оптимизация сетевой модели по критерию время – число исполнителей
После построения сетевого графика и определения его временных параметров проводят проверку соответствия полученных сроков продолжительности разработки нормативным или директивным срокам. Далее анализируют структуру сетевой модели, выявляя неоднородность напряженности работ проекта.
В настоящее время на практике сетевую модель вначале корректируют по времени, т. е. приводят ее к заданному сроку окончания проекта. Затем приступают к корректировке графика по критерию распределения ресурсов, начиная с трудовых ресурсов.
Минимизация числа исполнителей проекта при сохранении времени его выполнения
- минимизировать количество одновременно занятых исполнителей;
- выровнять потребность в трудовых ресурсах на протяжении всего срока выполнения проекта.
- перемещение работ по оси времени возможно осуществлять только вправо (откладывая их начало);
- работы критического пути трогать нельзя, т. к. это приведет к увеличению срока выполнения всего проекта;
- работы, имеющие свободный резерв времени, можно спокойно перемещать на величину этого резерва;
- перемещение работ, имеющих только полный резерв времени, требует аналогичного сдвига последующих работ;
- передвигаемые работы на линейной диаграмме выделяют, отмечая заметным символом: звездочкой, штрихом, цветом и т.п.
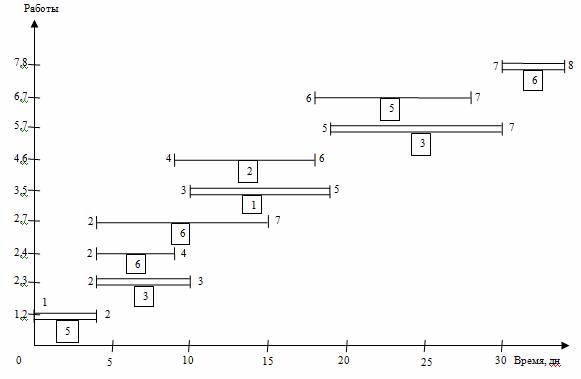
Рис. 1. Пример сетевого графика
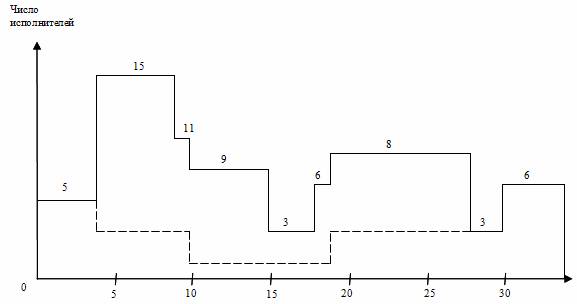
Проведем более детальный анализ линейной диаграммы и карты проекта с целью оптимизации трудовых ресурсов: выравнивая потребность в них на протяжении всего проекта и минимизируя количество одновременно занятых исполнителей. График ежедневной потребности ресурса показывает, что минимальное число исполнителей не может быть меньше 6 человек, что определяется их потребностью для работ критического пути. А 15 исполнителей на участке 5-10 дни проекта является явно завышенным и подлежит коррекции в первую очередь.
Рис. 2. Линейная диаграмма и карта проекта до оптимизации
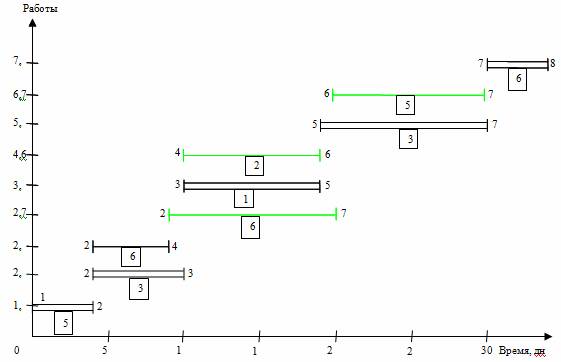
15 исполнителей заняты на работах 2,3; 2,4 и 2,7. Работу 2,3 трогать нельзя, т. к. это работа критического пути. Работа 2,4 имеет только полный резерв, но не имеет свободного резерва времени. Работа 2,7 имеет солидный свободный резерв времени и поэтому наиболее предпочтительна для оптимизации. Используем часть свободного резерва, переместив работу 2,7 (5-15 дни) на 5 дней (ее новый срок 10-20 дни). Тем самым максимально необходимое число исполнителей уменьшилось до 9 человек, т.е. задачу минимизации трудовых ресурсов проекта можно принять завершенной.
Рис. 3. Линейная диаграмма и карта проекта после оптимизации
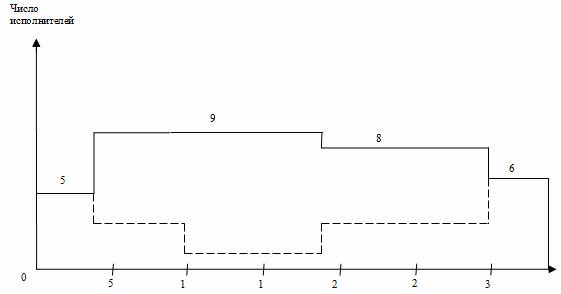
Далее решим задачу выравнивания потребности в ресурсах, анализируя интервалы времени, связанные с «провалами» карты проекта. С учетом перемещения работы 2,7 падения спроса на исполнителей в середине проекта (16-18 дни) уже не будет, но он останется ближе к концу проекта (29-30 дни). Чтобы сгладить график загрузки, переместим работу 6,7 (19-28 дни), имеющую свободный резерв времени, на 2 дня (новый срок 21-30 дни). Также для целей выравнивания потребности в трудовых ресурсах переместим работу 4,6 (10-18 дни) на 1 день (11-19 дни).
В итоге оптимизации приходим к линейной диаграмме и карте проекта, представленными на рис. 3. Из графика видно улучшение равномерности загрузки исполнителей: новая ежедневная потребность ресурса составляет от 5 до 9 человек в зависимости от этапа выполнения проекта, резких колебаний занятости нет. Длительность выполнения всего проекта при этом осталась неизменной (34 дня), т. е. необходимое условие оптимизации соблюдено. Видеоинструкция
3.4. Оптимизация сетевой модели
После расчета всех параметров сетевого графика производится его оптимизация. Сетевой график следует проанализировать с целью сокращения критического пути, затрат ресурсов, уменьшения ненужных резервов.
Под оптимизацией сетевой модели следует понимать процесс улучшения первоначального плана по различным показателям: времени, стоимости, количеству исполнителей.
Одним из методов оптимизации является выявление возможного сокращения выполнения работы и определение необходимых для этого затрат. При этом в зависимости от полноты решаемых задач оптимизация может быть частной и комплексной (полной). Видами частной оптимизации являются:
1) минимизация продолжительности выполнения разработки при заданной стоимости;
2) минимизация стоимости при заданной продолжительности.
Комплексная оптимизация — это нахождение такого варианта, при котором соотношения затрат и сроков выполнения в зависимости от конкретных целей были бы наилучшими, т.е. оптимальными. При комплексной (полной) оптимизации допускается повышение затрат при нормальном и экстренном (предельном) режиме работы с целью сокращения сроков или наоборот, увеличения сроков для обеспечения экономии затрат.
Краткая характеристика метода оптимизации
Все работы сетевой модели требуют различных затрат при нормальном и экстренном (предельном) режиме работы. Предельная продолжительность, т.е. минимально возможный срок проведения работы, требует больших затрат на ее проведение, чем при нормальном режиме работы.
Поэтому оптимизация сетевого графика по параметру «время-затраты» и предполагает нахождение такого плана выполнения комплекса работ, который обеспечивал бы достижение поставленной цели в наименьшие сроки и с минимальными затратами.
Оптимизацию следует осуществлять путем направленной корректировки последовательными «шагами» (итерациями). Шаги корректировки заключаются в последовательном сокращении сроков выполнения отдельных работ при минимальном увеличении их стоимости.
Сначала определяют все полные пути сетевой модели и рассчитывают их продолжительность. Определяют из них критический путь, как путь, имеющий наибольшую продолжительность.
Затем переходят к выполнению первой итерации.
Сокращают продолжительность критического пути до величины подкритического (максимального из оставшихся) по самой дешевой работе, уменьшая ее продолжительность. При этом увеличение стоимости будет минимальным. В результате 1-й итерации мы имеем два, одинаковой величины, критических пути, меньшие, чем первоначальный критический путь.
Теперь можно переходить ко 2-й итерации. Сокращаем продолжительность нескольких критических путей, полученных в ходе 1-й итерации, до подкритического по минимальной сумме затрат сокращаемых работ.
Далее процесс повторяется аналогичным образом до тех пор, пока существует возможность дополнительного сокращения продолжительности всех путей за счет уменьшения сроков выполнения наиболее дешевых работ.
Постоянно сравнивая предельные сроки выполнения работ критического пути с полученными в результате последней итерации результатами, останавливаемся тогда, когда убеждаемся, что дальнейшее сокращение всего комплекса работ невозможно.
Таким образом, относительно первоначального варианта продолжительность работ значительно сокращается, а затраты при этом увеличиваются относительно немного, этим достигается цель процесса оптимизации.