Сетевая модель, ее основные элементы
Объектами исследования методами СПУ являются крупные народнохозяйственные комплексы, научные исследования, конструкторская и технологическая подготовка производства новых видов изделий, строительство, реконструкция экономических объектов, капитальный ремонт основных фондов.
СПУ представляет собой совокупность расчетных методов, организационных и контрольных мероприятий по планированию и управлению комплексом работ.
Система СПУ позволяет:
— формировать календарный план реализации комплекса работ;
— выявлять резервы времени, трудовые, материальные и стоимостные ресурсы;
— осуществлять управление комплексом работ с прогнозированием и предупреждением возможных срывов в ходе работ;
— повышать эффективность управления в целом при четком распределении ответственности между руководителями разных уровней и исполнителями работ.
Комплекс работ (комплекс операций, проект) – всякая задача, для выполнения которой осуществляют разнообразные работы. Например, строительство здания, сборка самолета.
1. Составление перечня работ проекта, определение их логических связей и последовательности выполнения, закрепление работ за ответственными исполнителями, оценивание длительностей работ.
2. Реализация проекта в виде сетевого графика.
3. Упорядочение сетевого графика, расчет параметров работ, определение резервов времени и критического пути.
4. Анализ и оптимизация сетевого графика.
5. Составление временного графика реализации проекта.
Сетевая модель, ее основные элементы
Основой СПУ является сетевая модель.
Сетевой моделью называется экономико-математическая модель, отражающая для реализации некоторого проекта комплекс работ и событий, а также их логические и технологические последовательности и связи. Анализ сетевой модели, представленной в графической или табличной форме, позволяет:
— четко выяснить взаимосвязи этапов реализации проекта;
— определить наиболее оптимальный порядок выполнения этих этапов (например, для сокращения сроков выполнения всего комплекса работ).
Значит методы сетевого моделирования относятся к методам принятия оптимальных решений.
Математический аппарат сетевых моделей базируется на теории графов. Граф – это совокупность двух конечных множеств: множества точек, которые называются вершинами, и множества пар вершин, которые называются ребрами. Если рассматриваемые пары вершин являются упорядоченными, т.е. на каждом ребре задается направление, то граф называется ориентированным; в противном случае – неориентированным. Последовательность неповторяющихся ребер, ведущая от некоторой вершины к другой, образует путь. Граф называется связным, если для любых двух его вершин существует путь, их соединяющий; в противном случае граф называется несвязным. В экономике используются два вида графов: дерево и сеть. Дерево представляет собой связный граф без циклов, имеющий исходную вершину (корень) и крайние вершины; пути от исходной вершины к крайним вершинам называются ветвями. Сеть – это ориентированный конечный связный граф, имеющий начальную вершину (источник) и конечную вершину. Таким образом, сетевая модель представляет собой граф вида „ сеть”.
Сетевая модель в графическом изображении называется сетевым графиком. Ее отличительная особенность – четкое определение всех временных взаимосвязей предстоящих работ. Главные элементы сетевой модели – события и работы.
Термин работа используется в СПУ в широком смысле:
— это действительная работа – протяженный во времени процесс проекта, требующий затрат ресурсов (например, сборка изделия);
— это ожидание – протяженный во времени процесс, не требующий затрат труда (например, процесс сушки после покраски);
— это зависимость или фиктивная работа – логическая связь между двумя или несколькими работами (событиями), не требующими затрат труда, материальных ресурсов или времени. Эта связь указывает на тот факт, что возможность выполнения одной работы непосредственно зависит от результатов другой. Ее продолжительность принимается равной нулю (0).
Событие – это момент завершения какого-либо процесса, отражающий отдельный этап выполнения проекта. Событие устанавливает отношение предшествования среди процессов проекта. Оно может свершиться лишь тогда, когда закончатся все работы, ему предшествующие. Последующие работы могут начаться лишь тогда, когда событие свершится. Отсюда, двойственный характер события: для всех непосредственно предшествующих ему работ оно является конечным, а для всех непосредственно следующих за ним – начальным. При этом предполагается, что событие не имеет продолжительности и совершается как бы мгновенно.
В сетевой модели выделяют такие события:
— исходное – не имеет предшествующих работ и событий;
— завершающее – не имеет последующих работ и событий.
События на сетевом графике изображаются кружками (вершинами графа), а работы – стрелками (ориентированными дугами), указывающими связь между работами.
Принято под кодом (i,j) понимать работу, связывающую i -е событие с j -м событием. На рис. 4.1 показан фрагмент сетевого графика.
Рис. 4.1. Пример работ, события и кодирования работ
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Сетевая модель и её основные элементы
С математической точки зрения сетевой график— это связный взвешенный ориентированный граф без петель и контуров. Иногда сетевой график называют сетью. Основными понятиями сетевого планирования являются понятия работы и события. Работа – это любые действия , сопровождающиеся затратами ресурсов и времени и приводящие к определённым результатам. То есть, в сетевом планировании это понятие используется в широком смысле. Это и действительная работа, и ожидание, и зависимость или фиктивная работа, т. е. логическая связь между двумя или несколькими работами (событиями), не требующими затрат труда, ресурсов, времени. Фиктивная работа указывает, что возможность одной работы, непосредственно зависит от результатов другой. Естественно продолжительность фиктивной работы принимается равной нулю.
Событие – результат завершения одной или нескольких работ, отражающий отдельный этап выполнения проекта. Любая работа на сети может быть определена двумя событиями, между которыми она находится. Последующие работы могут начаться только тогда, когда событие свершится. Отсюда двойственный характер события: для всех непосредственно предшествующих ему работ оно является конечным, а для всех непосредственно следующих за ним- начальным. Предполагается, что событие не имеет продолжительности и свершается как бы мгновенно. Работы на сети изображаются дугами, а события – вершинами сети.
Порядок и правила построения сетевых графиков
Сетевые графики составляются на начальном этапе планирования. Построение и использование сетевых графиков производится в следующем порядке.
Вначале планируемый процесс разбивается на отдельные работы, составляется перечень работ и событий, продумываются их логические связи и последовательность выполнения, работы закрепляются за ответственными исполнителями.
Затем составляется сетевой график. При необходимости проводится его упорядочение, далее рассчитываются параметры событий и работ, определяются резервы времени и критический путь.
Наконец, проводятся анализ и оптимизация сетевого графика, который при необходимости вычерчивается заново с пересчетом параметров событий и работ.
При построении сетевого графика необходимо соблюдать ряд правил:
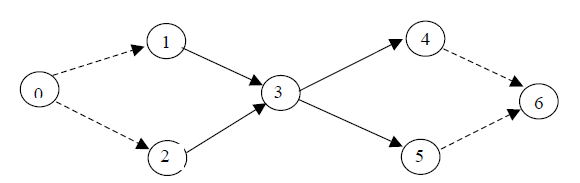
1. В сетевом графике рекомендуется иметь одно исходное и одно завершающее событие (по аналогии с рассмотренным ранее понятием сети).
Если это не так, то необходимо вводить фиктивные события и работы
(рис.1).
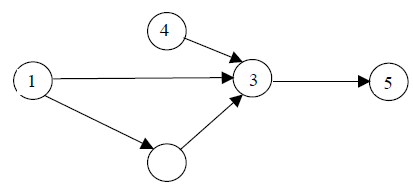
2. В сетевом графике не должно быть «хвостовых» событий (кроме исходного), которым не предшествует хотя бы одна работа (рис.2). Обнаружив в сети такое событие, необходимо определить исполнителей предшествующих им работ и включить эти работы в сеть.
Рис. 1.14
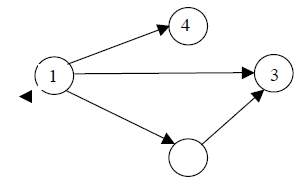
3. В сетевом графике не должно быть «тупиковых» событий, т.е. событий, из которых не выходит ни одна работа, за исключением завершающего события (рис.3).
Рис. 1.15
Здесь работа (1,3) или не нужна и её необходимо аннулировать, или не замечена необходимость определенной работы, следующей за событием 3.
Необходимо внимательное изучение взаимосвязей событий и работ для исправления сетевого графика.
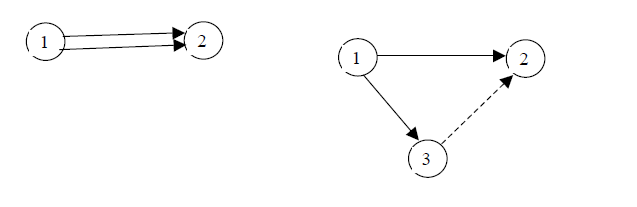
4. В сетевом графике не должно быть циклов, контуров и петель (рис.4).
Рис.1.16
При возникновении циклов и контуров, что довольно часто встречается в сложных сетях, необходимо вернуться к исходным данным и путем пересмотра состава работ добиться их устранения.
5.Любые два события должны быть связаны не более чем одной работой стрелкой. То есть, не должно быть параллельно выполняемых работ. Они или объединяются или вводятся фиктивные события и работы, которые изображаются на сетевом графике пунктиром (рис. 5). а) б)
Руководствуясь данными правилами, приступим к практическому
изучению вопросов построения и использования сетевых графиков в
соответствии с рассмотренным выше порядком.