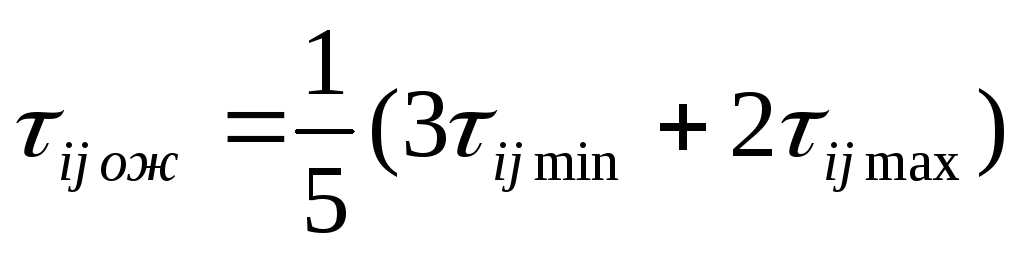Критический путь
Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующий за ней работы.
Полный путь L – любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим.
Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими также называются работы и события расположенные на этом пути. Работы этого пути определяют общий цикл завершения всего комплекса работ, планируемых при помощи сетевого графика. И для сокращения продолжительности проекта необходимо в первую очередь сокращать продолжительность работ, лежащих на критическом пути.
- Составить экономическое содержание задачи и перечислить перечень работ.
- Построить сетевой график и определить критический путь.
- Рассчитать параметры сетевого графика и поздние сроки поступления событий, резервы времени.
| Работа (i,j) | Количество предшествующих работ | Продолжительность tij | Ранние сроки: начало tij Р.Н. | Ранние сроки: окончание tij Р.О. | Поздние сроки: начало tij П.Н. | Поздние сроки:окончание tij П.О. | Резервы времени: полный tij П | Резервы времени: свободный tij С.В. | Резервы времени: событий Rj |
| (1,2) | 0 | 3 | 0 | 3 | 1 | 4 | 1 | 0 | 1 |
| (1,3) | 0 | 6 | 0 | 6 | 0 | 6 | 0 | 0 | 0 |
| (1,4) | 0 | 4 | 0 | 4 | 9 | 13 | 9 | 9 | 0 |
| (2,3) | 1 | 2 | 3 | 5 | 4 | 6 | 1 | 1 | 0 |
| (2,5) | 1 | 5 | 3 | 8 | 12 | 17 | 9 | 2 | 7 |
| (3,4) | 2 | 7 | 6 | 13 | 6 | 13 | 0 | 0 | 0 |
| (3,5) | 2 | 4 | 6 | 10 | 13 | 17 | 7 | 0 | 7 |
| (3,6) | 2 | 4 | 6 | 10 | 15 | 19 | 9 | 9 | 0 |
| (4,6) | 2 | 6 | 13 | 19 | 13 | 19 | 0 | 0 | 0 |
| (5,6) | 2 | 2 | 10 | 12 | 17 | 19 | 7 | 7 | 0 |
Критический путь: (1,3)(3,4)(4,6)
Продолжительность критического пути: 19 Перейти к онлайн решению своей задачи Пример . Рассчитать параметры сетевого графика мероприятия по совершенствованию системы управления. Сетевая модель задана таблично. Продолжительность выполнения работ дана в виде минимальной и максимальной оценок. Требуется вычислить табличным методом все основные характеристики работ и событий, найти критический путь и его продолжительность.
Скачать
Параметры сетевых моделей и методы их расчета
Сетевая модель имеет ряд характеристик, которые позволяют определить степень напряженности выполнения отдельных работ, а также всего их комплекса и принять решение о перераспределении ресурсов.
Ранний срок наступления события tр(i) — самый ранний из возможных сроков наступления события. Он равен продолжительности максимального пути от исходного события до данного.
tр(i) = max t[Lр(i)] (2.1)
Например, tр(7)=19, т.к. L1=(1,2,4,7), L2=(1,3,4,7),
t(L1)=5+12=17 < t(L2)=7+12=19.
Ранний срок начала работы tр.н.(i,j) равен продолжительности максимального пути от исходного до начального события данной работы.
tр.н.(i,j)=max t[Ln(i)](2.2)
Например, tр.н.(7,11)=19, т.к. L1=(1,2,4,7), L2=(1,3,4,7),
t(L1)=5+12=17
Ранний срок начала работы равен раннему сроку наступления начального события данной работы.
tр.н.(i,j) = tр(i) (2.3)
Ранний срок окончания работы tр.о.( i,j) равен сумме раннего срока начала работы и продолжительности данной работы.
tр.о.(i,j)= tр.н.(i,j) + t(i,j) (2.4)
Например, tр.о.(7,11)= tр.н.(7,11) + t(7,11)= 19+8=27.
Поздний срок наступления события tп( i) равен разности между продолжительностью критического пути и продолжительностью максимального пути от данного события до завершающего.
tп(i) =Tкр — max t[Lк(i)](2.5)
Например, tп(7)=19, т.к. L1=(7,11), L2=(7,9,11), t(L1)=8 > t(L2)=4,
tп(7) = Tкр — max t[Lк(7)]=27 — 8=19.
Для событий критического пути tр( i)=tп(i), для других событий tр(i)tп(i).
Поздний срок окончания работы tп.о.( i,j) – это самый поздний срок окончания работы, при котором планируемый срок окончания проекта не меняется, он равен разности между продолжительностью критического пути и продолжительностью максимального пути от конечного события данной работы до завершающего события.
tп.о.(i,j)=Tкр — max t[Lк(j)] (2.6)
Поздний срок окончания работы равен позднему сроку наступления конечного события tп.о.(i,j) = tп(j). Например, tп.о.(4,7) = tп(7)=19.
Поздний срок начала работы tп.н.( i,j) – самый поздний срок начала работы, при котором планируемый срок окончания проекта не меняется.
tп.н.(i,j)= tп .о.(i,j) — t(i,j) (2.7)
Например, tп.н.(4,7)= tп.о.(4,7) — t(4,7)=19-12=7.
Для работ критического пути ранние и поздние сроки начала и окончания работ равны: tр.н.(4,7)= tп.н.(4,7)=7, tр.о.(4,7)= tп.о.(4,7)=19.
Работы, не лежащие на критическом пути, могут иметь резервы времени.
Полный резерв времени Rп( i,j) – максимальное время, на которое можно увеличить продолжительность данной работы, не изменяя продолжительности критического пути.
Rп (i,j)= tп(j) — tр(i) — t(i,j)
Rп(i,j)= tп.н (i,j) — tр.н.(i,j) (2.8)
Rп (i,j)= tп.о.(i,j) — tр.о.(i,j)
Свободный резерв времени Rс( i,j) равен разности между ранним началом последующей работы и ранним окончанием рассматриваемой работы.
Rс(i,j)= tр.н (j,к) — tр.о.(i,j) (2.9) Перейти к онлайн решению своей задачи
Расчет и исследование сетевой модели
Расчет сетевой модели заключается в определении
- критического времени и критического пути;
- полных, независимых и частных резервов времени работ;
- резервов времени событий.
Удобно исследование сетевой модели изображать линейной диаграммой (графиком Ганта), в которой каждая работа – отрезок, параллельный оси времени. Длина этого отрезка равна продолжительности работы в выбранном масштабе. События i и j начала и конца работы uij ставят в начале и конце соответствующего отрезка. Отрезки располагают один над другим, снизу вверх, в порядке возрастания индексации. Момент наступления исходного события равен 0. Каждый отрезок (i,j) размещают на диаграмме таким образом, чтобы его начало совпало с самым правым концом всех отрезков, входящих в событие i. На рис. 2.11 представлена линейная диаграмма сетевого графика, изображенного на рис. 2.10. 










Лекция 2.3.3. Более сложные сетевые модели
Вероятностная временная сетевая модель
Второй также наиболее часто встречающейся сетевой моделью является одноцелевая временная вероятностная модель. Эта модель отличается тем, что продолжительности работ задаются как случайные величины. Такая модель более близка к условиям подсистемы ТПП. В настоящее время существуют две методики задания параметров распределения продолжительности работ:
- трехоценочная;
- двухоценочная.
При использовании первой методики эксперт задает 3 оценки продолжительности работы:
- оптимистическую τijmin;
- наиболее вероятную τijнв;
- пессимистическую τijmax.
Наиболее вероятная оценка – это время, необходимое для выполнения данной работы при нормальных, чаще всего встречающихся условиях (определяется первой). Оптимистическая оценка – это время, необходимое для выполнения работы при наиболее благоприятном стечении обстоятельств (определяется второй). Пессимистическая оценка – это время, необходимое для выполнения работ при неблагоприятных условиях. Как вы знаете, продолжительность работы связана с количеством ресурсов, выделяемых на ее проведение. Поэтому необходимо отметить, что для определения временных характеристик продолжительности работы эксперты должны руководствоваться максимальными значениями ресурсов. При использовании второй методики исключается наиболее вероятная оценка τijнв, определение которой вызывает у экспертов особые трудности и пользуются только двумя оценками τijmin и τijmax. На основе опытных данных установлено, что в большинстве случаев законы распределения продолжительностей работ обладают положительной асимметрией, распределение более круто в области τijmin. Это позволило из множества теоретических законов распределения выбрать закон β-распределения, кривая плотности которого имеет вид, представленный на рис.2.12. П





- ожидаемого времени выполнения работ τijож и оценки дисперсии σ 2 ij.
- всех временных параметров модели по тем же алгоритмам, что и у детерминированной временной модели, заменив τij на τijож.
Второй этап расчета заключается в определении вероятности наступления каждого события сети не позднее директивных сроков. Обозначим через μi – случайную величину, характеризующую ранний срок наступления события i. Если событие i связано с исходным событием лишь одним путем L(0i), то оценка математического ожидания μiопределяется суммой ожидаемых продолжительностей работ, принадлежащих этому пути tож[L(0i)], а оценка дисперсии σ 2 (μi) представляет собой сумму дисперсий продолжительностей тех же работ. В случае, если имеется более одного пути, предшествующего i-му событию, то упрощенно предполагается, что в этом случае μi и σ 2 (μi) вычисляется с использованием характеристик предшествующего пути, имеющего максимальную продолжительность max t[L(0i)]. Если же несколько путей имеют максимальную продолжительность, то для определения дисперсии выбирается путь с максимальной дисперсией продолжительности, так как он характеризуется большой неопределенностью, а, следовательно, дает более надежный результат. Т