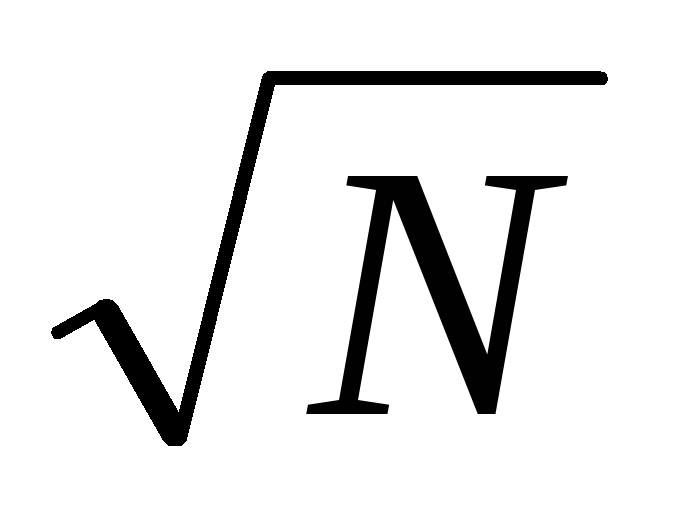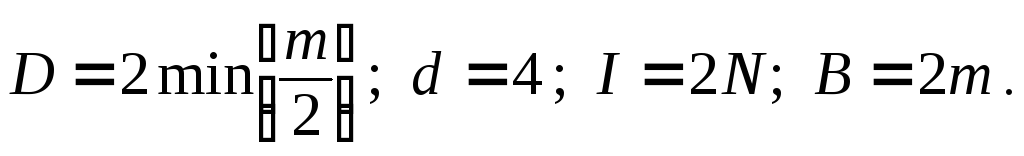Новосибирский государственный университет
Словарь терминов в коллекции «Вычислительные системы»
Древовидная топология
Древовидная топология (tree) — построение сети по схеме двоичного дерева, где каждый узел более высокого уровня связан с двумя узлами следующего по порядку более низкого уровня.
В древовидной топологии сеть строится по схеме так называемого строго двоичного дерева, где каждый узел более высокого уровня связан с двумя узлами следующего по порядку более низкого уровня. Узел, находящийся на более высоком уровне, принято называть родительским , а два подключенных к нему нижерасположенных узла — дочерними . В свою очередь, каждый дочерний узел выступает в качестве родительского для двух узлов следующего более низкого уровня. Каждый узел связан только с двумя дочерними и одним родительским.
Такую сеть можно охарактеризовать следующими параметрами: D = 2log 2 [( N +1)/2]; d = 1 для краевых узлов, d = 2 для корневого узла и d = 3 для остальных узлов; I = N -1; В = 1. Диаметр для двоичного дерева возрастает пропорционально лишь логарифму числа узлов, в то время как степень узла остается постоянной. Сеть с такой топологией хорошо масштабируется. Основной недостаток топологии — малая ширина бисекции, что предполагает ограниченную полосу пропускания.
Топология двоичного дерева была использована в мультипроцессорной системе DADO из 1023 узлов, разработанной в Колумбийском университете.
При больших объемах пересылок между несмежными узлами древовидная топология оказывается недостаточно эффективной, поскольку сообщения должны проходить через один или несколько промежуточных звеньев. Очевидно, что на более высоких уровнях сети вероятность затора из-за недостаточно высокой пропускной способности линий связи выше. Этот недостаток устраняют с помощью топологии, называемой «толстым» деревом.
Идея «толстого» дерева состоит в увеличении пропускной способности коммуникационных линий на прикорневых уровнях сети. С этой целью на верхних уровнях сети родительские и дочерние узлы связывают не одним, а несколькими каналами, причем чем выше уровень, тем больше число каналов. На рисунке это отображено в виде множественных линий между узлами верхних уровней. Топология «толстого» дерева реализована в вычислительной системе СМ-5.
- Цилькер Б.Я. Организация ЭВМ и систем: учебник для вузов / С.А. Орлов, Б.Я. Цилькер. — СПб.: Питер, 2011. — 688 с.
Литература
Ключевые термины: статическая топология; размер сети; число связей; диаметр сети; степень узла; пропускная способность сети; задержка сети; связность сети; ширина бисекции сети; полоса бисекции сети; 
Федотова Ольга
НГУ
ФИТ НГУ
ИВТ СО РАН © 2012-2023, Новосибирский государственный университет, Новосибирск
© 2004-2023, Институт вычислительных технологий СО РАН, Новосибирск
© 2004-2023, Федотов А.М.
Дата последней модификации: 14.08.2013
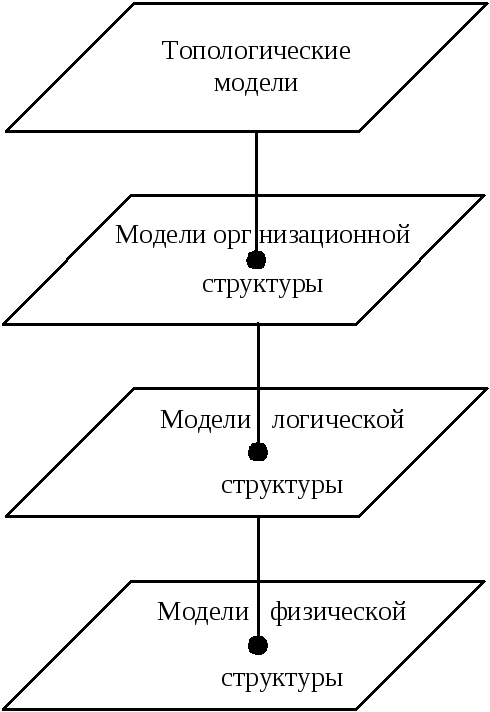
Топологические модели
На уровне самого общего представления любая сеть состоит из совокупности пунктови соединяющих их линий,взаимное расположение которых характеризует связность сети и способность к обеспечению информационного обмена между различными адресатами. Структура, отображающая расположение пунктов сети и связывающих их линий называетсятопологией сети. Различаютфизическую топологию илогическую.Физическая топологияотображает размещение пунктов в пространстве и конфигурацию линий связи.Логическая топологиядает представление о путях перемещения информационных сообщений в сети от источников к приемнникам на основе адресной информации.
Рисунок 1. Системное описание архитектуры сети
Для исследования топологических особенностей сети ее удобно изображать в виде точеки соединяющих их дуг. Такая геометрическая фигура носит название граф. Точки в графе именуются вершинами, а дуги, если не учитывается их направленность, – ребрами. Граф является моделью топологической структуры информационной сети. Выбор топологии является наипервейшей задачей, решаемой при построении сети. Он осуществляется с учетом таких требований, какэкономичность инадежность связи. Задача выбора топологии сети решается сравнительно несложно, если известен набортиповых топологий (примитивов), которые можно использовать как отдельно, так и в комбинации. Рассмотрим ряд таких типовых топологий, назовем их базовыми, и охарактеризуем их особенности.
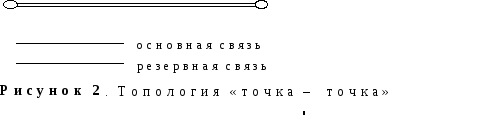
Топология «точка –точка»является наиболее простым примером базовой топологии и представляет собой сегмент сети, связывающий физически и логически два пункта (рис 2).
Надежность связи в таком сегменте может быть повышена за счет введения резервной связи, обеспечивающей стопроцентное резервирование,
называемое защитой типа 1+1. При выходе из строя основной связи сеть автоматически переводится на резервную. Несмотря на всю простоту, именно эта базовая топология наиболее широко используется при передаче больших потоков информации по высокоскоростным магистральным каналам, например, по трансокеанским подводным кабелям, обслуживающим цифровой телефонный трафик. Она же используется как составная часть радиально-кольцевой топологии (в качестве радиусов). Топология «точка–точка» с резервированием типа 1+1 может рассматриваться как вырожденный вариант топологии «кольцо» (см. ниже).
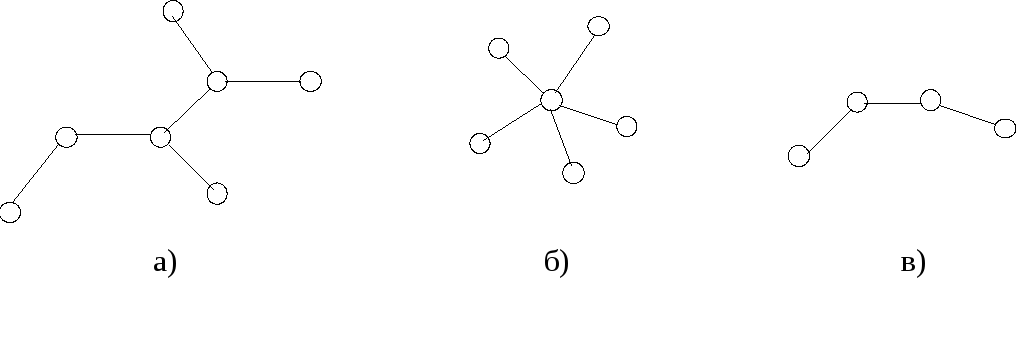
Древовидная топологияможет иметь различные варианты (рис. 3).
Рисунок 3. Древовидная топология: а – дерево, б – звезда, в – цепь
Особенностью сегмента сети, имеющего древовидную топологию любого из перечисленных вариантов, является то, что связность nпунктов на уровне физической топологии здесь достигается числом ребер R = n – 1, что обеспечивает высокую экономичность такой сети. На логическом уровне, количество связывающих путей передачи информации между каждой парой пунктов в таком сегменте всегда равно h = 1. С точки зрения надежности, это достаточно низкий показатель. Повышение надежности в таких сетях достигается введением резервных связей (например, защиты типа 1+1). Древовидная топология находит применение в локальных сетях, сетях абонентского доступа.
Топология «кольцо»(рис. 4) характеризует сеть, в которой к каждому пункту присоединены две, и только две линии. Кольцевая топология широко используется в локальных сетях, в сегментах меж-узловых соединений территориальных сетей, а также в сетях абонентского доступа, организуемых на базе оптического кабеля.
Число ребер графа, отображающего физическую топологию, равно числу вершин: R = n и характеризует сравнительно невысокие затраты на сеть.
На логическом уровне между каждой парой пунктов могут быть организованы h = 2 независимых связывающих пути (прямой и альтернативный). Это обеспечивает повышение надежности связи в таком сегменте, особенно при использовании резервирования типа 1+1, так называемогодвойного кольца(рис. 5). Двойное кольцо образуется физическими соединениями между парами пунктов, при которых информационный поток направляется в двух противоположных направлениях (восточном и западном), причем одно направление используется как основное, второе – как резервное.
Полносвязная топология(рис. 6) обеспечивает физическое и логическое соединение пунктов по принципу «каждый с каждым». Граф, включающий nвершин, содержитR = n (n – 1)/2 ребер, что определяет высокую стоимость сети. Количество независимых связывающих путей между каждой парой пунктов в таком сегменте сети равноh = n – 1. Полносвязная топология на логическом уровне обладает максимальной надежностью связи, благодаря возможности организации большого числа обходных путей. Такая топология характерна для территориальных сетей при формировании сегментов базовых и опорных (магистральных) сетей. Максимальная надежность связи в сегменте достигается при использовании на обходных направлениях альтернативных сред распространения сигналов (например, волоконно-оптический кабель и радиорелейная линия).
Ячеистая топология(рис. 7). Каждый пункт сегмента имеет непосредственную связь с небольшим числом пунктов, ближайших по расстоянию. При большом числе вершин число реберR » r×n/2, гдеr– число ребер, инцидентных каждой вершине. Ячеистые сегменты обладают высокой надежностью связи при меньшем числе ребер по сравнению с полно-связным сегментом.
Рисунок.7 Ячеистая топология
Использование полно-связной и ячеистой топологий целесообразно лишь в сегментах с высокой концентрацией трафика, так как их реализация связана со значительными затратами.
Сложные топологии.Реальные сети часто имеют сложные топологии, являющиеся расширениями и/или комбинациями базовых физических топологий. За счет использования сложных топологий удается обеспечивать требования красширяемостиимасштабируемости сети.
Под расширяемостьюпонимают возможность увеличения размера сети, путем сравнительно несложного включения новых структурных элементов.Расширяемость сети, как правило, ограничена, т.к. начиная с некоторого момента добавление очередного структурного элемента приводит к резкому снижению производительности сети.
Хорошо масштабируемые сети характеризуются неограниченными возможностями по наращиванию сети, не оказывающими влияния на ее производительность. Хорошая масштабируемость является одним из важнейших требований, предъявляемых к современным сетям, особенно территориальным.
4. Древовидные топологии
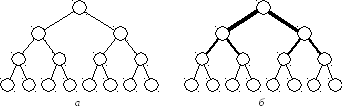
Сеть с древовидной топологией(рис. 5.4,a) строится по схеме строго двоичного дерева, где каждый узел более высокого уровня связан с двумя узлами следующего по порядку более низкого уровня. Узел, находящийся на более вы-соком уровне, называетсяродительским, а два подключенных к нему нижерас-положенных узла –дочерними. В свою очередь, каждый дочерний узел выступает в качестве родительского для двух узлов следующего более низкого уровня. Каждый узел связан только с двумя дочерними и одним родительским.
Рис. 5.4. Древовидная топология: а– стандартное дерево;б– «толстое» дерево
Древовидная сеть характеризуется следующими параметрами: 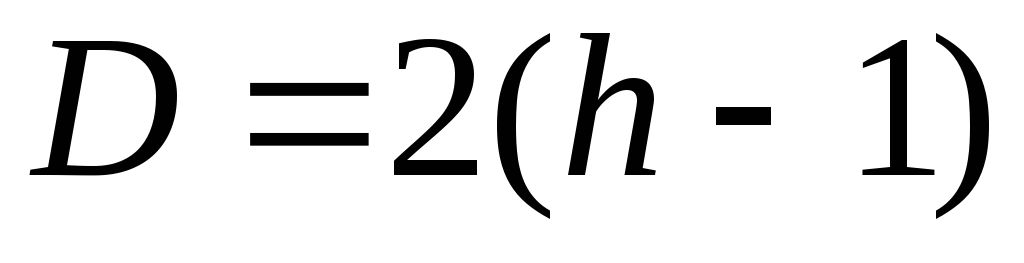
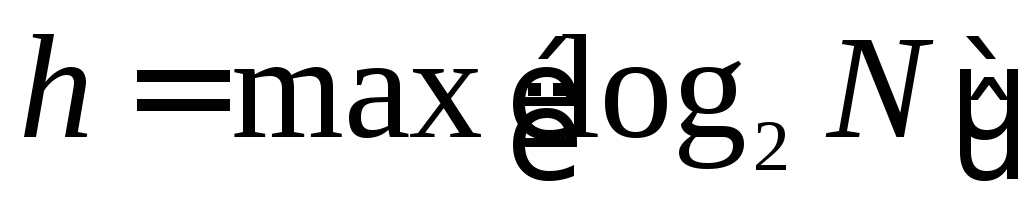
При больших объемах пересылок между несмежными узлами древовидная топология недостаточно эффективна, поскольку сообщения должны проходить через один или несколько промежуточных звеньев. Очевидно, что на более высоких уровнях сети вероятность затора из-за недостаточно высокой пропуск-ной способности линий связи выше. Этот недостаток устраняется с помощью топологии, называемой «толстым» деревом (рис. 5.4,б).
Идея «толстого» дерева состоит в увеличении пропускной способности коммуникационных линий на прикорневых уровнях сети. С этой целью на верх-них уровнях сети родительские и дочерние узлы связываются не одним, а не-сколькими каналами, причем чем выше уровень, тем больше число каналов. На рис. 5.4, бэто отображено в виде множественных линий между узлами верхних уровней. Топология «толстого» дерева реализована в вычислительной системе СМ-5.
5. Решетчатые топологии
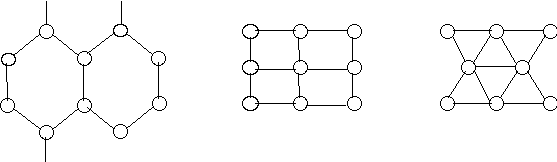
Решетчатые(mesh) топологии ВС ориентированы на решение научно-технических задач, связанных с обработкой массивов. Их конфигурация опреде-ляется видом и размерностью массива.
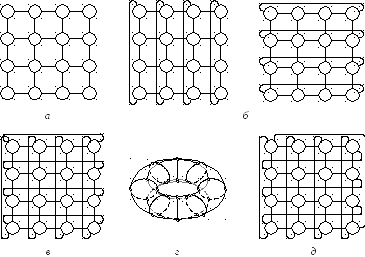
Рис. 5.5. Решетчатые топологии: а– плоская;б – цилиндрическая;
в–г – тороидальная;д– витая тороидальная
Простейшими примерами для одномерных массивов служат цепочка и кольцо. Для двумерных массивов данных наиболее подходит топология плоской прямоугольной матрицы узлов, каждый из которых соединен с ближайшим сосе-дом (рис. 5.5, а). Такая сеть размерностиm×m(m=) имеет следующие харак-теристики:D= 2(m – 1);d = 4;I = 2N – 2m;B=m.
Если провести операцию свертывания(wraparound) плоской матрицы, соединив информационными трактами одноименные узлы левого и правого столбцов или одноименные узлы верхней и нижней строк плоской матрицы, то из плоской конструкции получится топология типа цилиндра (рис. 5.5,б). В то-пологии цилиндра каждый ряд (или столбец) матрицы представляет собой коль-цо. Если одновременно произвести свертывание плоской матрицы в обоих на-правлениях, то получим тороидальную топологию сети (рис. 5.5,в). Двумерный тор на базе решеткиm×m обладает следующими параметрами:
Объемный вид тороидальной топологии для массива размерности 4×8 показан на рис. 5.5, г.
Помимо свертывания к плоской решетке может быть применена операция скручивания(twisting). Суть этой операции состоит в том, что вместо колец все узлы объединяются в разомкнутую или замкнутую спираль, то есть узлы, рас-положенные с противоположных краев плоской решетки, соединяются с неко- торым сдвигом. Если горизонтальные петли объединены в виде спирали, обра-зуется сеть типаILLIAC. На рис. 5.5,дпоказана подобная конфигурация СМС, соответствующая хордальной сети четвертого порядка и характеризуемая сле-дующими метриками:D=m – 1;d = 4;I = 2N;B= 2m.
Трехмерная сеть реализована в архитектуре суперЭВМ Cray T3D и пред-ставляет собой трехмерный тор, образованный объединением процессоров в кольца по трем координатам: x,y иz.
Примерами ВС, где реализованы различные варианты решетчатых топо-логий, служат: ILLIAC IV,MPP,DAP,CM-2,Paragonи др.