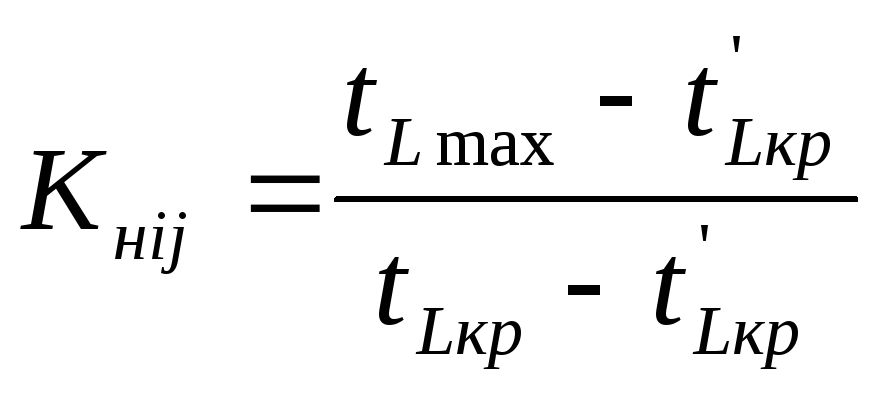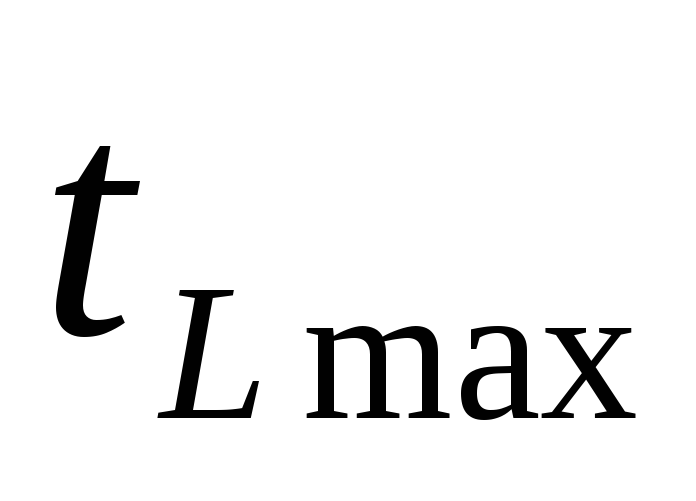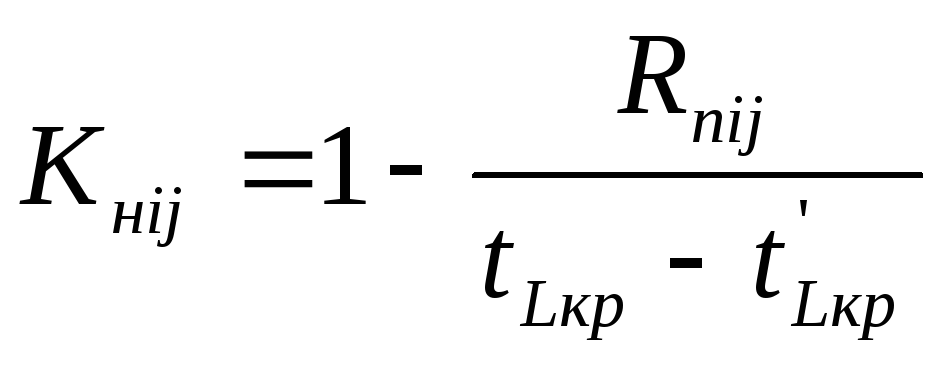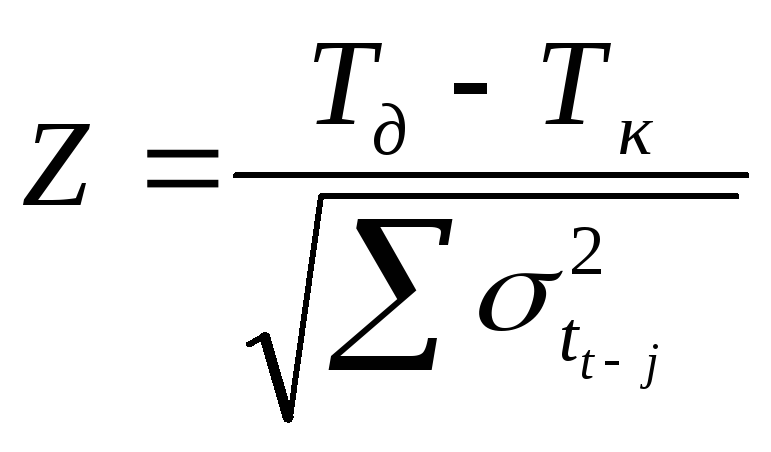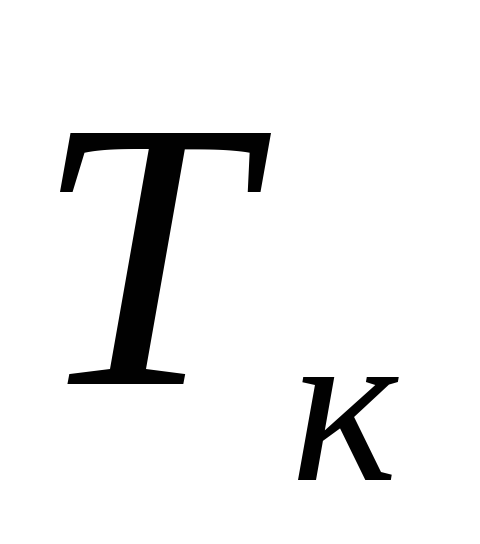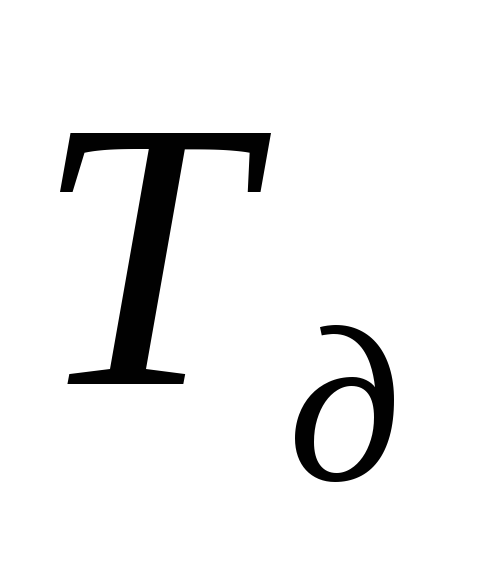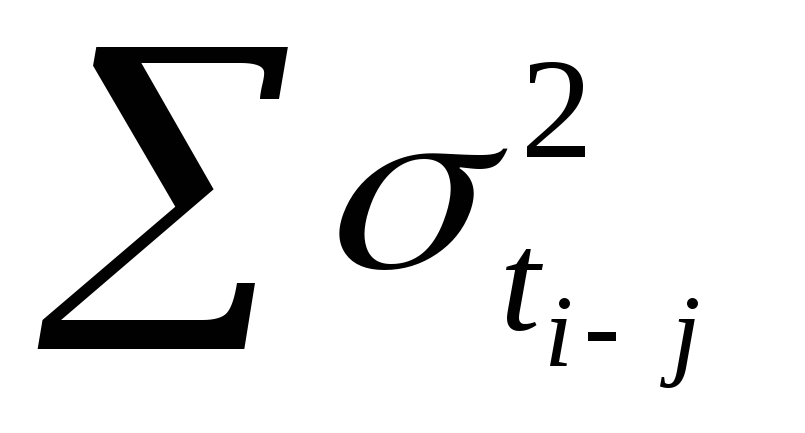Оптимизация сетевых моделей
После того как сетевой график построен и рассчитаны его основные показатели, приступают к его оптимизации, т.е. к последовательной корректировке сети для достижения наиболее эффективных результатов и заданных параметров по времени и ресурсам. Для этого проводится анализ сетевых графиков.
В итоге оптимизация сетевых графиков заключается в улучшении процессов планирования, организации и управления комплексом работ с целью сокращения расходования экономических ресурсов и повышения финансовых результатов при заданных плановых ограничениях.
В практике оптимизация сетевых графиков подразделяется на частную и комплексную.
Основными видами частной оптимизации являются два экономических подхода:
1) минимизация времени выполнения комплекса планируемых работ при заданной стоимости проекта;
2) минимизация стоимости всего комплекса работ при заданном времени выполнения проекта.
Комплексная оптимизация сетевых моделей состоит в нахождении наилучших соотношений показателей затрат экономических ресурсов и сроков выполнения планируемых работ применительно к определенным производственным условиям и ограничениям. В рыночных отношениях в качестве критерия оптимальности сетевых систем планирования могут быть выбраны такие важные экономические показатели, как максимальная прибыль (финансовый результат) от производства товаров и услуг, минимальный расход ресурсов на реализацию планов, максимальная производительность труда исполнителей, минимальные затраты рабочего времени на достижение конечной цели и т.д.
Рассмотрим основные подходы и методы к оптимизации сетевых графиков.
Оптимизация сетевого графика по времени заключается в сокращении его критического пути в соответствии с директивными сроками окончания комплекса работ. Это может быть достигнуто за счет следующих мероприятий:
· сокращения времени выполнения критических работ за счет переброски ресурсов с некритических работ, располагающих значительным резервом времени. Этот шаг основан на анализе временных показателей графика и не требует больших затрат материальных и финансовых ресурсов. Анализ сети проводится с целью выравнивания продолжительности наиболее напряженных путей. Рассчитываются коэффициенты напряженности любого полного пути (отношение его длительности к критическому пути), которые позволяют классифицировать работы по зонам: критическую (Кн>0,8), подкритическую (0,6£ Кн £0,8), резервную (Кн<0,6); чем ближе коэффициент к единице, тем сложнее выполнить работу;
· изменения топологии сети в результате внедрения новой технологии производства работ, позволяющей находить новые последовательности и взаимосвязи работ;
· расчленения длительных работ на отдельные части и замены последовательных работ параллельными.
После сокращения критического пути за счет проведения тех или иных мероприятий заново пересчитываются параметры сетевого графика, чтобы выявить достаточность принятых мер и проверить, не появились ли новые критические пути.
Оптимизация сетевых моделей за счет минимизации расходования материальных ресурсов сводится к определению оптимальных норм расхода ресурсов на единицу выполненной работы или распределению имеющихся ресурсов на весь комплекс работ. Одним из возможных способов сокращения критического пути может служить перераспределение различных ресурсов с ненапряженных путей на выполнение критических работ. При этом следует также иметь в виду тот факт, что сверхплановое насыщение критических работ ресурсами не беспредельно, так как существуют определенные ограничения в ресурсах на каждом предприятии.
Важнейшей комплексной проблемой оптимизации сетевых графиков является минимизация стоимости, которая характеризует наименьшие суммарные издержки на осуществление всего комплекса запланированных работ. При этом методе исходят из того экономического предположения, что величина издержек на выполнение той или иной работы находится при прочих равных условиях в обратной зависимости от затрат рабочего времени на ее выполнение. Если все запланированные работы будут выполняться с рассчитанной в сетевом графике точностью, то общая стоимость разработанного плана-проекта будет минимальной. С ускорением работ затраты возрастают, а с их замедлением — снижаются. Причем при минимальной продолжительности работ их стоимость становится максимальной и, наоборот, при максимальной длительности затраты будут минимальными.
5.6. Комплексное планирование производства и материально-технического снабжения на основе сетевого планирования
Комплексное планирование производства и его материально-технического снабжения на основе сетевых моделей обеспечивает координацию всех планируемых процессов, позволяет рассматривать их в динамике и вычислять календарные нормативы.
Территориальная разобщенность поставщиков и потребителей, периодичность производства необходимых материалов, возможность нарушения нормальных сроков изготовления материалов и транспортного процесса, а также другие факторы вызывают необходимость опережения процесса материально-технического снабжения по отношению к производственным процессам.
При комплексном сетевом планировании производства и его снабжения поставка материалов, конструкций, оборудования и других ресурсов, так называемые «внешние работы», отражается в сетевом графике сплошными стрелками, на которых обозначено время материального опережения и которые выходят из двойных кружков (рис. 5.6).
Рис. 5.6. Пример изображения «внешних работ»
Материальное опережение на сетевых графиках выражается в относительных показателях (дни, часы), которые характеризуют время пребывания материальных ресурсов (его ожидание использования при выполнении работ) в виде производственных запасов. Материальное опережение показывает время, необходимое для раннего завоза материалов на склады предприятий или на строительные площадки по отношению к срокам их потребления. Материальное опережение (М0) вычисляется по формуле (5.1).
где Зт, З, Зп – текущий, страховой и подготовительный запасы в относительном выражении.
Для расчета сроков начала подготовки материалов на базах снабжения необходимо знать время, затрачиваемое на подсортировку, комплектование и транспортировку материалов и на оформление документов, которое можно рассчитать по формуле (5.2).
где tп, tу, tт,tо.д — соответственно время, затраченное на подготовку, комплектование, транспортировку и оформление документов.
Сроки завоза на склады снабжения предприятий с единичным производством или на строительные площадки определяется по формуле (5.3).
где tзав(ij) – наиболее поздний допустимый срок завоза материалов для выполнения работы (ij); tр(ij) – наиболее ранний срок начала работы (ij); М0 — нормативная величина материального опережения.
Самый поздний срок начала подготовки материалов на базах снабжения можно определить по формуле (5.4).
где M0+Д – продолжительность работ по выполнению поставки с баз снабжения на склад предприятия и на строительную площадку.
При серийном машиностроительном производстве материалы завозятся на склады предприятий партиями. При этом размер партии значительно выше потребности разового запуска материала в производство. В данных условиях сроки завоза материалов на склады предприятий tзав(ij) можно рассчитать по формуле (5.5).
где tр(ij) – самый ранний срок начала работ (ij); Оk – остаток k- го материала на складах предприятия к началу производства серии машин в натуральных единицах измерения; n – количество поступивших партий k- го материала до момента завоза очередной (n +1)-й партии; Пk – величина партии поставки k- го материала в натуральных единицах измерения; Pk(ij) – потребность в k- ом материале для выполнения (ij) работы в натуральных единицах измерения; М0 – постоянная часть материального опережения.
На основании данных формул увязываются сроки завоза материалов и сроки подготовки материалов на базах снабжения с календарными сроками выполнения работ по сетевому графику. Это дает возможность планировать работу складского хозяйства снабженческо-сбытовых организаций и работу транспорта.
ТЕМА 6. ПЛАНИРОВАНИЕ ПРОИЗВОДСТВА
5.Анализ и оптимизация сетевых моделей.
С учетом рассчитанных параметров необходимо оценить целесообразность структуры сетевого графика, внести возможные изменения. Пересоставление графика может сводиться к устранению лишних работ, более целесообразному расчленению работ, установления параллельности выполнения работ.
Анализ сетевого графика предусматривает расчет коэффициентов напряженности работ Кнij:
(3.17)
где — продолжительность максимального пути, проходящего через данную работу;
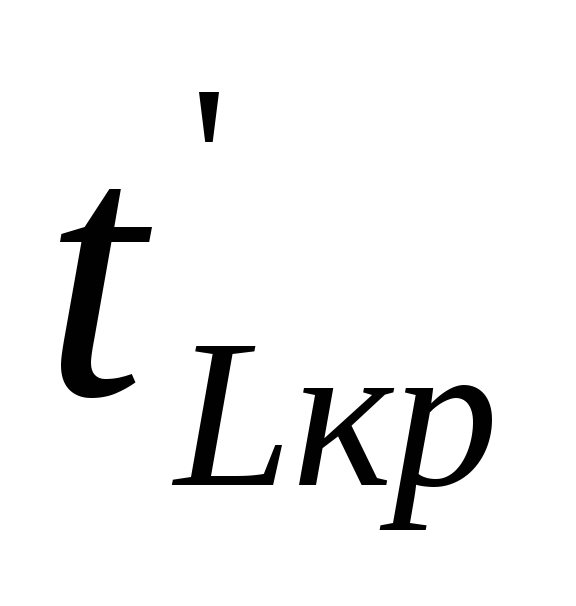
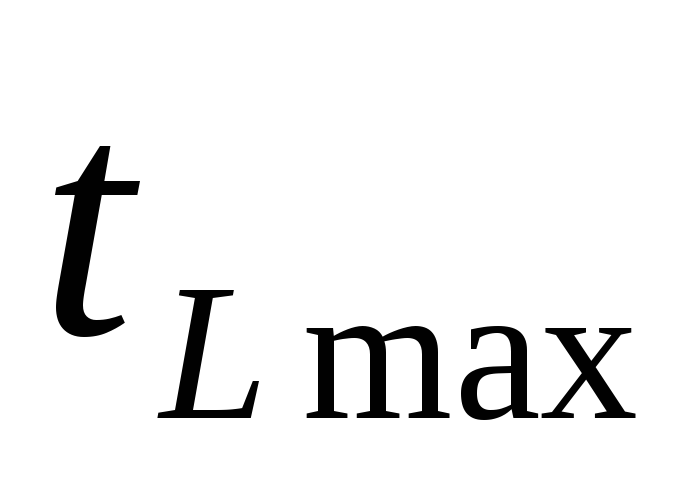
(3.18)
Рассчитанные коэффициенты следует внести в последнюю графу табл. 3.4.
Расчет позволяет распределить все работы по зонам (критическая, подкритическая, резервная).
Следующей задачей анализа является определение вероятности свершения завершающего события в заданный срок (Рк).
(3.19)
где -аргумент функции нормального распределения вероятностей;
— срок свершения завершающего события по расчету (t ) в днях;
— заданный (директивный) срок свершения завершающего события, дн.;
— сумма дисперсии работ, лежащих на критическом пути.
При Рк 0,35 опасность нарушения заданного срока свершения завершающего события настолько велика, что необходимо повторное планирование с перераспределением ресурсов. В этом случае необходима оптимизация сетевого графика по времени. Она проводится путем переброски ресурсов с ненапряженных путей на критический, что приводит к сокращению его продолжительности.
При Рк 0,65 можно считать, что на работах критического пути имеются избыточные ресурсы и, следовательно, общая продолжительность работ может быть сокращена.
Таблица 12.5 – таблица значений функции нормального распределения вероятностей
Оптимизация сетевого графика может быть направлена на решение различных задач, в частности:
а) сокращение критического пути до директивного срока выполнения комплекса работ;
б) минимизация численности исполнителей.
в) минимизация затрат при заданном времени. Наиболее широко используется первое направление.
Методы оптимизации также могут быть различными. В процессе оптимизации необходимо ориентироваться на коэффициенты напряженности работ, виды ресурсов, необходимых для выполнения работ (квалификация работников, виды оборудования, источники финансирования и др.), величины резервов работ и их виды (полный, частный, свободный).
Оптимизация с целью сокращения критического пути может быть выполнена с помощью графика
0


1
Условные обозначения: Т – технологи;
Работы располагаются: а) слева направо в последовательности их выполнения (начальных и конечных событий, которые обозначаются шифрами) в определенном масштабе;
б) снизу вверх в порядке убывания коэффициентов напряженности без соблюдения масштаба.
На критическом пути или прямой, представляющей его продолжение, наносится точка, 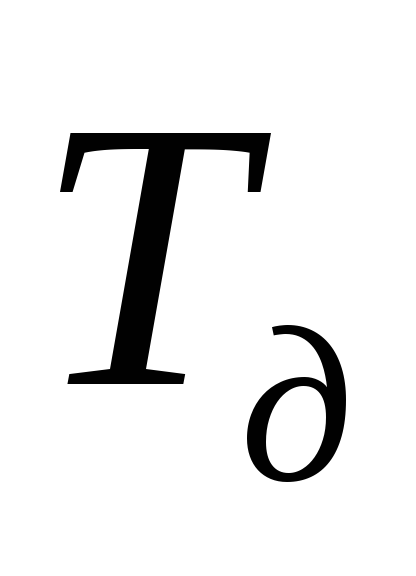
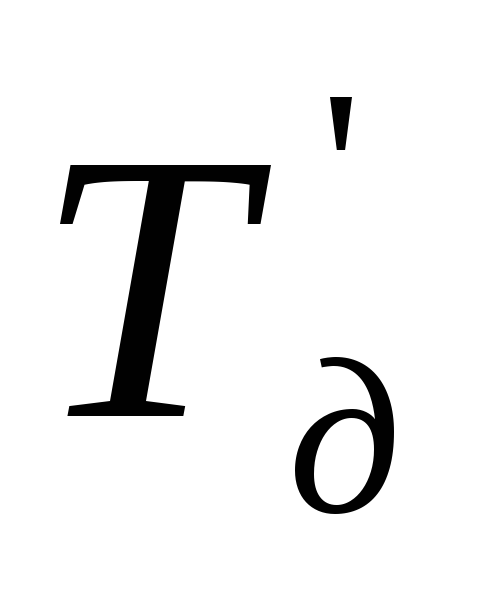
С помощью условных обозначений (цвета, букв, шифров) на графике наносится вид ресурсов каждой работы или только работ, имеющих аналогичные ресурсы.
С ненапряженных работ ресурсы перераспределяются на работы критического и подкритического путей. При изъятии ресурсов с какой-либо работы рассчитывается время ее удлинения. Оно сравнивается с величинами резервов этой работы с учетом их вида и использования на других работах данного пути. Увеличение времени работы должно быть меньше ее полного резерва или части полного резерва времени работы, оставшейся после изъятия ресурсов других работ данного пути.
Оптимизация сетевого графика при ограниченных ресурсах требует составления линейной диаграммы и графика ежедневной потребности ресурсов.
После перегруппировки ресурсов возможно изменение топологии сетевого графика. Тогда производится перешифровка работ, и измененные шифры вносятся в перечень работ (таблица 12.1). Затем следует пересчет параметров сетевого графика, анализ с определением коэффициентов напряженности и дальнейшая оптимизация, если она возможна.
После первой оптимизации следует определить, насколько сократился критический путь и исчерпаны ли возможности оптимизации.
Если в результате оптимизации критический путь станет равен директивному сроку или меньше его, то можно оставить полученный вариант графика. Если же критический путь остается больше директивного срока, то необходимо рассчитать потребность в дополнительных ресурсах для сокращения критического пути на величину равную Тд — tlkp