Элементы сетевой модели и их виды

18. Назначение сетевых моделей и сетевых графиков классификация и элементы сетевых графиков

Основным методом решения плановых и управленческих задач в строительстве является метод сетевого планирования и управления (СПУ). Он включает построение, расчет, анализ и оптимизацию сетевых моделей и применяется для решения задач, связанных с планированием и управлением в строительстве.

Сетевой моделью называется ориентированный граф, отражающий последовательность и организационно-технологическую связь между ра­ботами.

Сетевые модели используются в строительстве для решения задач пер­спективного планирования, определения продолжительности и сроков выполнения основных этапов создания объектов, а также планирования капитальных вложений по периодам строительства.

Сетевая модель, представленная графически на плоскости с рассчи­танными временными и ресурсными параметрами называется сетевым графиком.

Сетевые модели классифицируются по следующим признакам: 1. По виду целей— одноцелевые (строительство одного объекта); многоцелевые (строительство организацией нескольких объектов).

2. По числу охвата объектов — частная модель; комплексная модель.

3. По характеру оценки параметров — детерминированная (с заранее и полностью обусловленными данными); вероятностная (с учетом слу­чайных факторов).

4. Модели с учетом целевой направленности— временные, ресурс­ные, стоимостные.

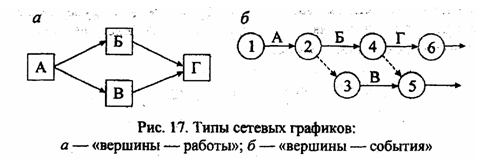
Сетевые графики бывают двух типов (рис. 17):

В дальнейшим мы будем работать с сетевыми графиками типа «вер­шины— события».

Элементы сетевого графика представлены в табл.

Таблица Элементы сетевого графика

Работа— производственный процесс, требующий затрат времени и ресурсов. На графике над стрелкой пишется наименование работы, под стрелкой — ее продолжительность (рис. 18, а).

Ожидание — процесс, требующий только затрат времени (выдержка бетона).

Зависимость — вводится в сетевой график для правильной взаимосвя­зи работ (рис. 18, б). Необходимость в ней диктуется технологией или ограничением материально-технических ресурсов.

Событие —- факт или момент окончания одной или нескольких работ, необходимый и достаточный для начала работ последующих.

Событие, не имеющее предшествующих работ, называется начальным, событие, не имеющее последующих работ, — конечным.

Путь— непрерывная последовательность работ (по направлению стрелок) от начального до конечного события. Путь наибольшей продол­жительности называется критическим и определяет срок строительства.

19. Правила построения сетевых графиков алгоритм расчета сетевого графика секторным методом. Оптимизация сетевых графиков

Прежде чем составлять сетевой график, следует определить, на сколь­ко захваток делится строящийся объект, и по возможности сохранить чис­ло и границы захваток по всем видам работ или делать их (в случае край­ней необходимости) кратными друг другу. В таблицу исходных данных вписывают работы по каждой захватке за исключением захваток, равных по трудоемкости и по объемам, тогда достаточно перечислить одну за­хватку, а ниже написать: «Вторая захватка — то же».

Составлять график следует по принципу: окончание каких работ должно послужить началом следующих.

Основные правила построения сетевых моделей следующие.

1. Нумерация событий производится слева направо и сверху вниз, но­мер присваивается событию, к которому не приходит ни одна стрелка из ранее не пронумерованного (пустого). При этом не должно быть повто­ряющихся номеров событий. Не допускается, чтобы разные работы (стрелки) имели одинаковый шифр.

2. В сетевом графике не допускается замкнутого контура работ, что легко выявляется, если соблюдать указанное выше правило нумерации.

Наличие замкнутых контуров свидетельствует об ошибке в построе­нии либо в составлении исходных данных.

3. Не должно быть тупиковых работ.

4. Зависимости (фиктивные работы) используются в графике для от­ражения взаимосвязей между работами.

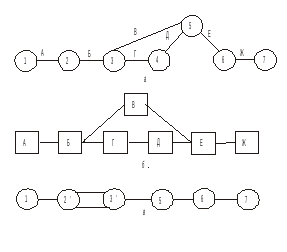
5. При построении сетевого графика на строительство здания, имею­щего число захваток больше двух, события средних цепочек нужно рас­кладывать через холостую связь во избежание ложных зависимостей

Для работы А на третьей захватке необязательно окончание работы Б на первой и так далее, поэтому события средней цепочки следует разло­жить,

6. При составлении графика желательно иметь направление стрелок слева направо и избегать их пересечения.

Расчет ведется непосредственно на графике. Для этого каждое событие делится на четыре сектора, в которых указываются все необходимые для расчета данные о работе и событиях графика.

Сначала определяют ранние начала работ, которые записываются в ле­вом секторе четырехсекторного события. Ранние начала работ, выходя­щих из первого события, принимают равными нулю (ранние начала ис­ходных работ).

Раннее начало любой другой работы равно наибольшей из сумм ран­них начал и продолжительностей предшествующих работ, т. е. наиболь­шему раннему окончанию.

Таким образом, последовательно от исходного события до завершаю­щего определяются все ранние начала работ. Завершающее событие рас­сматривается как начальное событие условной работы с нулевой продол­жительностью.

Поздние окончания работ определяются справа налево, причем позд­нее окончание завершающих работ равно наибольшему из ранних их окончаний.

Позднее окончание любой работы сетевого графика равно наименьшей из разностей поздних окончаний последующих работ и их продолжительностей.

Все работы, входящие в одно событие, имеют одинаковые поздние окончания.

Разница значений правого и левого секторов дает нам величину общих резервов событий, которые записываются в знаменателе нижнего сектора. На этом заканчивается расчет графика.

Критический путь определяется по событиям, ранние и поздние сроки свершения которых (числа в правых и левых секторах) равны между со­бой.

Оптимизация сетевых графиков.

Для оптимизации сетевых графиков по ресурсам Имеются следующие алгоритмы:

1. Рациональное распределение ограниченных ресурсов.

2. Минимизация максимального потребления ресурсов в единицу времени.

3. Минимизация неравномерностей потребления ресурсов, т. е. лик­видация «пиков» и «провалов».

Все эти алгоритмы дают возможность сократить суммарное потребле­ние ресурсов в единицу времени без увеличения продолжительности критического пути сетевого графика. Наиболее эффективным по времени, затрачиваемому на расчеты, является алгоритм минимизации максималь­ного потребления ресурсов в единицу времени.

Алгоритм минимизации максимального потребления ресурсов, заключается в постепенном снижении максимального потребления ресурсов.

Источник

1. Сетевая модель и ее основные элементы.

Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ (операций), заданного в специфической форме сети, графическое изображение которой называется сетевым графиком. Отличительной особенностью сетевой модели является четкое определение всех временных взаимосвязей предстоящих работ.

Главными элементами сетевой модели являются событиями и работы

Термин работа используется в СПУ в широком смысле.Во-первых, это действительная работа — протяженный во временипроцесс, требующий затрат ресурсов (например, сборка изделия, испытание прибора и т.п.). Каждая действительная работа, должна быть конкретной, четко описанной и иметь ответст­венного исполнителя.

Во-вторых, это ожидание — протяженный во времени процесс,не требующий затрат труда (например, процесс сушки после окраски, старения металла, твердения бетона и т.п.).

В-третьих, это зависимость, или фиктивная работа — логическая связь между двумя или несколькими работами (события), не требующими затрат труда, материальных ресурсов или времени. Она указывает, что возможность одной работы непосредственно зависит от результатов другой. Естественно, что продолжительность фиктивной работы принимается равной нулю.

Событие — это момент завершения какого-либо процесса, отражающий отдельный этап выполнения проекта. Событие может являться частным результатом отдельной работы или суммарным результатом нескольких работ. Событие может свершиться только тогда, когда закончатся все работы, ему предшествующие. Последующие работы могут начаться только тогда, когда событие свершится. Отсюда двойственный характер события: для всех непо­средственно предшествующих ему работ оно является конечным, а для всех непосредст­венно следующих за ним — начальным. При этом предполагается, что событие не имеет продолжительности и свершается как бы мгновенно. Поэтому каждое событие, включаемое в сетевую модель, должно быть полно, точно и всесторонне определено, его формулировка должна включать в себя результат всех непосредственно предшествующих ему работ.

Среди событий сетевой модели выделяют исходное и завершающее события. Исходное собы­тие не имеет предшествующих работ и событий, относящихся к представленному в модели комплексу работ. Завершающее событие не имеет последующих работ и событий.

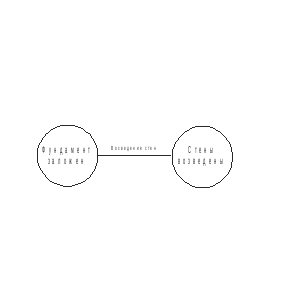
События на сетевом графике (или, как еще говорят, на графе)изображаются кружками (вершинами графа), а работы — стрелками(ориентированными дугами), показывающими связь между работами. Пример фрагмента сетевого графика представлен на рис 1:

На рис. 2, а приведен сетевой график задачи моделирования и построения оптималь­ного плана некоторого экономического объекта. Чтобы решить эту задачу, необходимо провести следующие работы: А – сформулировать проблему исследования; В5 — матема­тическую модель изучаемого объекта; В — собрать информацию; Г — выбрать метод решения задачи; Д — построить и отладить программу для ЭВМ; Е — рассчитать опти­мальный план; Ж — передать результаты расчета заказчику. Цифрами на графике обозначены номера событий, к которым приводит выполнение соответствующих работ.

Из графика, например, следует, что работы В и Г можно начать выполнять независимо одна от другой только после свершения события 3, т.е. когда выполнены работы А и Б; работу Д — после свершения события 4, когда выполнены работы А, Б и Г; а работу Е можно выполнить только после наступления события 5, т.е. при выполнении всех предшествующих ему работ А, Б, В, Г и Д.

В сетевой модели, представленной на рис. 2 а, нет числовых оценок. Такая сеть называется структурной. Однако на практике чаще всего используются сети, в которых заданы оценки про­должительности работ (указываемые в часах, неделях, декадах, месяцах и т.д. над соответствую­щими стрелками), а также оценки других параметров, например трудоемкости, стоимости и т.п. Именно такие сети мы будем рассматривать в дальнейшем.

Но прежде сделаем следующее замечание. В рассмотренных примерах сетевые графики со­стояли из работ и событий. Однако может быть и иной принцип построения сетей — без событий. В такой сети вершины графа (например, изображенные прямоугольниками) означают определен­ные работы, а стрелки — зависимости между этими работами, определяющие порядок их выполнения. В качестве примера сетевой график «события — работы» задачи моделирования и построе­ния оптимального плана некоторого экономического объекта, приведенный на рис. 2 а, пред­ставлен в виде сети «работы — связи» на рис. 2 б. А сетевой график «события — работы» той же задачи, но с неудачно составленным перечнем работ, представлен на рис. 2 в (см. правило 3 в разд. 3).

Следует отметить, что сетевой график «работы — связи» в отличие от графика «события — ра­боты» обладает известными преимуществами: не содержит фиктивных работ, имеет более про­стую технику построения и перестройки, включает только хорошо знакомое исполнителям понятие работы без менее привычного понятия события. Вместе с тем сети без событий оказываются значительно более громоздкими, так как событий обычно значительно меньше, чем работ (пока­затель сложности сети, равный отношению числа работ к числу событий, как правило, существенно больше единицы). Поэтому эти сети менее эффективны с точки зрения управления ком­плексом. Этим и объясняется тот факт, что (при отсутствии в целом принципиальных различий между двумя формами пред­ставления сети) в настоящее время наибольшее распространение получили сетевые графики «со­бытия — работы».

Источник