Правила построения сетевых графиков
Для построения сетевого графика необходимо выявить последовательность и взаимосвязь работ: какие работы необходимо выполнить, и какие условия обеспечить, чтобы можно было начать данную работу, какие работы можно и целесообразно выполнять параллельно с данной работой, какие работы можно начать после окончания данной работы. Эти вопросы позволяют выявить технологическую взаимосвязь между отдельными работами, обеспечивают логическое построение сетевого графика и его соответствие моделируемому комплексу работ.
Уровень детализации сетевого графика зависит от сложности строящегося объекта, количества используемых ресурсов, объёмов работ и продолжительности строительства.
Имеется два типа сетевых графиков:
Сетевые графики типа «вершины — работы».
Элементами такого графика являются работы и зависимости. Работа представляет собой определенный производственный процесс, требующий затрат времени и ресурсов для его выполнения, и изображается прямоугольником. Зависимость (фиктивная работа) показывает организационно-технологическую связь между работами, не требующую затрат времени и ресурсов, изображается стрелкой. Если между работами имеется организационный или технологический перерыв, то на зависимости указывается длительность этого перерыва. Пример сетевого графика «вершины — работы» приведен на рис. 6.1.
Рис. 6.1. Сетевой график типа «вершины — работы»
Если работа сетевого графика «вершины — работы» не имеет предшествующих работ, то она является исходной работой этого графика. Если работа не имеет последующих работ, то она является завершающей работой сетевого графика. В сетевом графике «вершины — работы» не должно быть замкнутых контуров (циклов), т.е. зависимости не должны возвращаться в ту работу, из которой они вышли.
Сетевые графики типа «вершины-события».
Элементами такого типа графиков являются работы, зависимости и события. Работа изображается сплошной стрелкой, зависимость – пунктирной. Событие представляет собой результат одной или нескольких работ, необходимый и достаточный для начала одной или нескольких последующих работ, и изображается кружком.
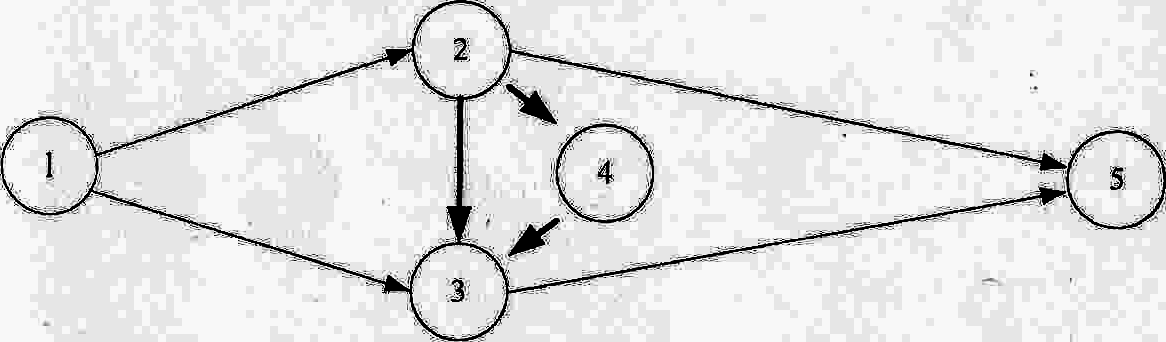
В сетевых графиках этого типа каждая работа находится между двумя событиями: начальным, из которого она выходит, и конечным, в которое она входит. События сетевого графика нумеруются, поэтому каждая работа имеет код, состоящий из номеров её начального и конечного события. Например, на рис. 6.2 работы закодированы как (1,2); (2,3); (2,4); (4,5).
Рис.6.2. Сетевой график «вершины — события»
Если событие сетевого графика «вершины-события» не имеет предшествующих работ, то оно является исходным событием этого графика. Следующие непосредственно за ним работы называются исходными. Если событие не имеет последующих работ, то оно является завершающим событием. Входящие в него работы называются завершающими.
Для правильного отображения взаимосвязей между работами необходимо соблюдать следующие основные правила построения сетевого графика «вершины-события»:
1. При изображении одновременно или параллельно выполняемых работ (например, работ «Б» и «В» на рис.6.2) вводятся зависимость (3,4) и дополнительное событие (3).
2. Если для начала работы «Г» необходимо выполнить работы «А» и «Б», а для начала работы «В» – только работу «А», то вводится зависимость и дополнительное событие (рис.6.3.).
Рис.6.3. Изображение зависимости между работами
3. В сетевом графике не д.б. замкнутых контуров (циклов), т.е. цепочки работ, возвращающейся к тому событию, из которого они вышли (рис.6.4).
Рис. 6.4. Пример замкнутого контура (2,4,3,2)
4. В сетевом графике при поточной организации строительства вводятся дополнительные события и зависимости (рис. 6.5.).
Рис. 6 5. Пример изображения потоков однородных работ
3. Упорядочение сетевого графика. Понятие о пути.
Предположим, что при составлении некоторого проекта выделено 12 событий: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и 24 связывающие их работы: (0, I), (0, 2), (0, 3), (1, 2), (1, 4), (1, 5), (2, 3), (2, 5), (2, 7), (3, 6), (3, 7), (3, 10), (4, 8), (5, 8), (5, 7), (6, 10), (7, 6), (7, 8), (7, 9), (7, 10), (8, 9), (9, II), (10, 9), (10, II). Необходимо составить и упорядочить сетевой график.
Как следует из перечня работ, исходным событием сетевого графика является событие 0 (ему не предшествуют никакие работы), а завершающим — событие 11 (за ним не следует ни одна работа). Полагая на сетевых графиках изменение времени слева направо, поместим событие 0 в левую часть графика, а событие 11 — в правую часть, разместив между ними промежуточные события в некотором порядке, соответствующем их номерам (рис. 4). События свяжем работами-стрелками в соответствии с перечнем работ.
Построенный сетевой график удовлетворяет сформулированным в разд. 3 правилам, предъявляемым к его построению. Однако этот график не полностью упорядочен.
Упорядочение сетевого графика заключается в таком расположении событий и работ, при котором для любой работы предшествующее ей событие расположено левее и имеет меньший номер по сравнению с завершающим эту работу событием. Другими словами, в упорядоченном сетевом графике все работы-стрелки направлены слева направо: от событий с меньшими номерами к событиям с большими номерами.
Разобьем условно сетевой график на несколько вертикальных слоев (обводим их пунктирными линиями и обозначаем римскими цифрами).
Поместив в I слое начальное событие 0 (рис. 5), мысленно вычеркнем из графика (см. рис. 4) это событие и все, выходящие из него работы-стрелки. Тогда без входящих стрелок останется событие 7, образующее II слой. Вычеркнув мысленно событие 1 и все выходящие из него работы, увидим, что без входящих стрелок остаются события 4 и 2, которые образуют III слой. Продолжая указанную процедуру вычеркивания, получим IV слой с событиями 5 и 3, V слой — с событием 7, VI слой—с событиями 8 и 6, VII слой — с событием 10, VIII слой—с событием 9 и, наконец, IX слой — с событием 11.
Теперь видим, что первоначальная нумерация событий не совсем правильная: так, событие 6 лежит в VI слое и имеет номер, меньший, чем событие 7 из предыдущего слоя. То же можно сказать о событиях 9 и 10.
Изменим нумерацию событий в соответствии с их расположением на графике (см. рис. 5) и получим упорядоченный сетевой график (рис. 6), в котором над стрелками указана продолжительность соответствующих работ (в сутках).
Одно из важнейших понятий сетевого графика — понятие пути. Путь — любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы. Среди различных путей сетевого графика наибольший интерес представляет полный путь L — любой путь, начало которого совпадает с исходным событием сети, а конец — с завершающим.
Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими называются также работы и события, расположенные на этом пути.
Порядок нумерации событий, расположенных в одном вертикальном слое, принципиального значения не имеет, так что нумерация одного и того же сетевого графика может быть неоднозначной.
Например, для рассматриваемого нами сетевого графика (см. рис. 6) полными путями будут:
путь 

путь 0




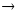
путь 0



путь 0




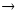
Можно убедиться в том, что последний путь имеет наибольшую продолжительность (не только среди приведенных четырех полных путей, но и среди всех полных путей, которых в данном случае насчитывается 64), поэтому он и является критическим (способ определения критического пути, не основанного на переборе всех полных путей сетевого графика, приводится в разд. 5). Продолжительность критического пути составляет 61 сутки, т.е. для проведения комплекса работ понадобятся 61 сутки. Быстрее комплекс выполнить нельзя, так как для достижения завершающего события критический путь надо пройти обязательно.
Действительно, для достижения события 11 надо выполнить работу (10, 11), т.е. достичь события 10; для достижения события 10 надо провести работу (9, 10), т.е. достичь события 9; для достижения события 9 надо провести работу (6, 9), т.е. достичь события 6, и т.д.
Определив критический путь, мы тем самым установили критические события сети 0, 3, 5, 6, 9, 10 и 11 и критические работы (0, 3), (3, 5), (5, 6), (6, 9), (9, 10), (10, 11).
Критический путь имеет особое значение в системе СПУ, так как работы этого пути определяют общий цикл завершения всего комплекса работ, планируемых при помощи сетевого графика. И для сокращения продолжительности проекта необходимо в первую очередь сокращать продолжительность работ, лежащих на критическом пути.
Следует отметить, что классический вид сетевого графика — это сеть, вычерченная без масштаба времени. Поэтому сетевой график, хотя и дает четкое представление о порядке следования работ, но недостаточно нагляден для определения тех работ, которые должны выполняться в каждый данный момент времени. В связи с этим небольшой проект после упорядочения сетевого графика рекомендуется дополнить линейной диаграммой проекта. Такая линейная диаграмма для рассматриваемой сети показана на рис. 7.
При построении линейной диаграммы каждая работа изображается параллельным оси времени отрезком, длина которого равна продолжительности этой работы. При наличии фиктивной работы нулевой продолжительности (в рассматриваемой сети ее нет) она изображается точкой. События i и j, начало и конец работы (i, j) помещают соответственно в начале и конце отрезка. Отрезки располагают один над другим, снизу вверх в порядке возрастания индекса i, а при одном и том же i — в порядке возрастания индекса j (на рис. 7 вследствие ограниченности места не показаны работы-отрезки, выходящие из 2-, 3-, 4- и 5-го событий).
По линейной диаграмме проекта можно определить критическое время, критический путь, а также резервы времени всех работ (см. об этом в разд. 5).
Так, критическое время комплекса работ равно координате на оси времени самого правого конца всех отрезков диаграммы:
(сутки).
Для определения критического пути рассматриваем работы — отрезки, конечные события которых совпадают с завершающим событием сети (в нашем примере (9, 11) и (10, 11)). Затем находим отрезок (9, 10), правый конец которого лежит на одной вертикали с левым концом одного из рассматриваемых ранее отрезков (10, 11). Аналогично определяем и другие работы-отрезки критического пути: (6, 9), . (0, 3) (на рис. 7 все они выделены жирным шрифтом).