Графический метод оптимизации сетевой модели

Графический метод оптимизации сетевой модели — «время-затраты»

Метод «время-затраты» заключается в установлении оптимального соотношения между продолжительностью и стоимостью работ.

Определение затрат и ресурсов, необходимых для выполнения каждой работы, производится после разработки сетевого графика.

Таким образом, материальные и трудовые ресурсы планируются на основе общей структуры сети, созданной с помощью прогнозирования временных оценок.

Для построения графиков «время-затраты» (рис. 4.3) для каждой работы задаются:

• минимально возможные денежные затраты на выполнение работы (при условии выполнения работы за нормальное времяt_н);
• минимально возможное время выполнения работы t_мин при максимальных денежных затратах .

Рис. 4.3. График «время-затраты« При определении первой пары оценок упор делается на максимальное сокращение затрат, а при определении второй — на максимальное сокращение времени. Приближенно определить размеры дополнительных затрат, необходимых для сокращения срока выполнения работы, или решить обратную задачу возможно с помощью графика с аппроксимирующей прямой. Величина дополнительных денежных затрат, необходимых для выполнения работы в сокращенное время t_c, составит (4.23) Для каждого вида работ рассчитывается и строится свой график, характеризующийся наклоном аппроксимирующей прямой. Используя линейную зависимость «затраты-время» для каждого вида работ, можно вычислить коэффициент возрастания затрат на единицу времени: (4.24) Экономическая эффективность от внедрения СПУ определяется в первую очередь возможностями уменьшения общего цикла работ и сокращением затрат за счет более рационального использования трудовых, материальных и денежных ресурсов. Кроме того, целесообразность использования при разработке нормативов сетевых моделей подтверждается и тем, что в процессе реализации на ЭВМ сетевой модели в каждом конкретном случае может быть получен оптимальный план-график проведения работ. Нормативный показатель, сопровождаемый таким планом-графи­ком, помимо своих основных функций, является еще и незамени­мым для управления ходом разработки. Таким образом, использование метода нормирования с помощью сетевых моделей позволяет достаточно точно имитировать процесс разработки государственного стандарта и в соответствии с этим получить достоверные нормативные показатели, оптимальный план-график проведения работ, обеспечивающий наиболее рацио­нальное использование имеющихся ресурсов и, наконец, усовер­шенствовать управление разработками, контролируя соответствие фактического состояния работ рассчитанному оптимальному план-графику. Первым этапом процесса нормирования является детальный анализ трудовых процессов и составление их описания. Далее целесообразно составление схемы процедуры, которая в дополнение к описанию процесса разработки стандарта позволит выявить характер проводимых работ, их последовательность, кате­горию исполнителя, виды документов, используемых при разра­ботке и получаемых в результате проведения работ. Разработчик обеспечивает дос­тупность проекта национального стандарта заинтересованным ли­цам для ознакомления, дорабатывает его с учетом полученных в письменной форме замечаний и проводит публичное обсуждение проекта национального стандарта. Схема дальнейшего движения проекта национального стандарта вплоть до принятия представлена на рис. 4.4. Рис. 4.4. Порядок принятия национального стандарта ПРОЦЕДУРА № 1 Разработка технического задания (рис. 4.5)

Источник

Оптимизация сетевой модели по критерию время – число исполнителей

После построения сетевого графика и определения его временных параметров проводят проверку соответствия полученных сроков продолжительности разработки нормативным или директивным срокам. Далее анализируют структуру сетевой модели, выявляя неоднородность напряженности работ проекта.
В настоящее время на практике сетевую модель вначале корректируют по времени, т. е. приводят ее к заданному сроку окончания проекта. Затем приступают к корректировке графика по критерию распределения ресурсов, начиная с трудовых ресурсов.

Минимизация числа исполнителей проекта при сохранении времени его выполнения

• минимизировать количество одновременно занятых исполнителей;
• выровнять потребность в трудовых ресурсах на протяжении всего срока выполнения проекта.

• перемещение работ по оси времени возможно осуществлять только вправо (откладывая их начало);
• работы критического пути трогать нельзя, т. к. это приведет к увеличению срока выполнения всего проекта;
• работы, имеющие свободный резерв времени, можно спокойно перемещать на величину этого резерва;
• перемещение работ, имеющих только полный резерв времени, требует аналогичного сдвига последующих работ;
• передвигаемые работы на линейной диаграмме выделяют, отмечая заметным символом: звездочкой, штрихом, цветом и т.п.

Рис. 1. Пример сетевого графика

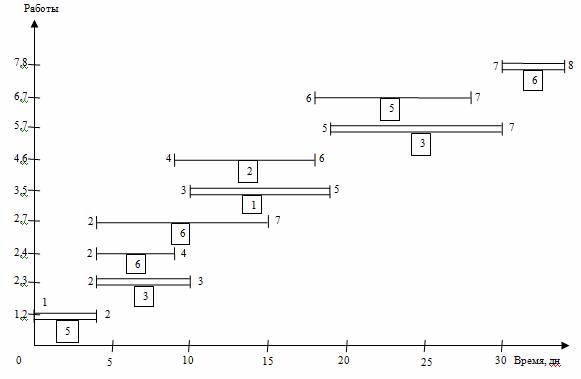
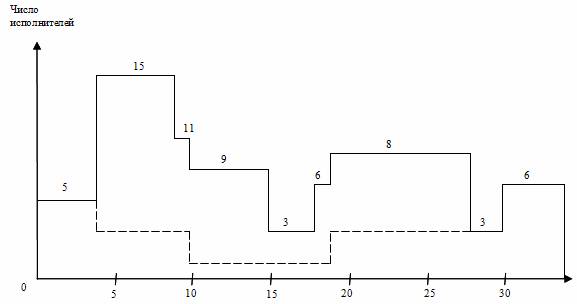
Проведем более детальный анализ линейной диаграммы и карты проекта с целью оптимизации трудовых ресурсов: выравнивая потребность в них на протяжении всего проекта и минимизируя количество одновременно занятых исполнителей. График ежедневной потребности ресурса показывает, что минимальное число исполнителей не может быть меньше 6 человек, что определяется их потребностью для работ критического пути. А 15 исполнителей на участке 5-10 дни проекта является явно завышенным и подлежит коррекции в первую очередь.

Рис. 2. Линейная диаграмма и карта проекта до оптимизации

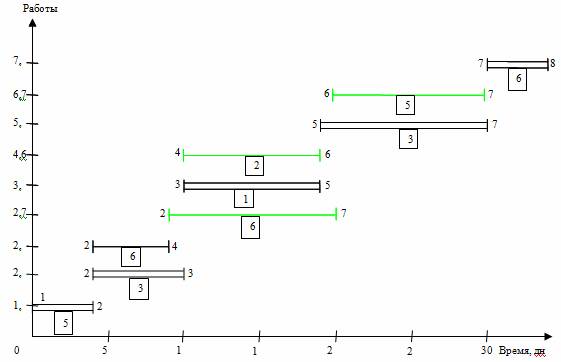
15 исполнителей заняты на работах 2,3; 2,4 и 2,7. Работу 2,3 трогать нельзя, т. к. это работа критического пути. Работа 2,4 имеет только полный резерв, но не имеет свободного резерва времени. Работа 2,7 имеет солидный свободный резерв времени и поэтому наиболее предпочтительна для оптимизации. Используем часть свободного резерва, переместив работу 2,7 (5-15 дни) на 5 дней (ее новый срок 10-20 дни). Тем самым максимально необходимое число исполнителей уменьшилось до 9 человек, т.е. задачу минимизации трудовых ресурсов проекта можно принять завершенной.

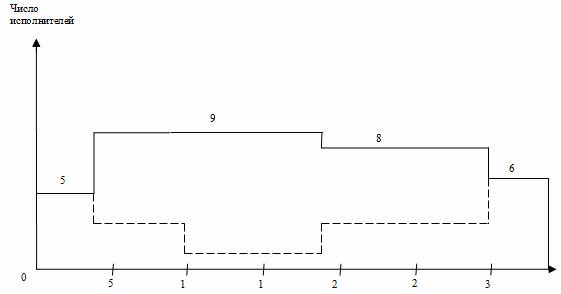
Рис. 3. Линейная диаграмма и карта проекта после оптимизации
Далее решим задачу выравнивания потребности в ресурсах, анализируя интервалы времени, связанные с «провалами» карты проекта. С учетом перемещения работы 2,7 падения спроса на исполнителей в середине проекта (16-18 дни) уже не будет, но он останется ближе к концу проекта (29-30 дни). Чтобы сгладить график загрузки, переместим работу 6,7 (19-28 дни), имеющую свободный резерв времени, на 2 дня (новый срок 21-30 дни). Также для целей выравнивания потребности в трудовых ресурсах переместим работу 4,6 (10-18 дни) на 1 день (11-19 дни).
В итоге оптимизации приходим к линейной диаграмме и карте проекта, представленными на рис. 3. Из графика видно улучшение равномерности загрузки исполнителей: новая ежедневная потребность ресурса составляет от 5 до 9 человек в зависимости от этапа выполнения проекта, резких колебаний занятости нет. Длительность выполнения всего проекта при этом осталась неизменной (34 дня), т. е. необходимое условие оптимизации соблюдено. Видеоинструкция

Источник

Графический метод расчета параметров сетевого графика

Рассчитать параметры сетевой модели графическим (секторным) методом можно через калькулятор.

Помимо него существуют следующие способы расчета: табличный метод, метод потенциалов.

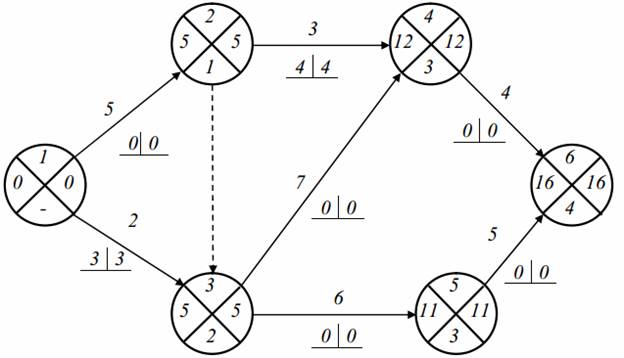
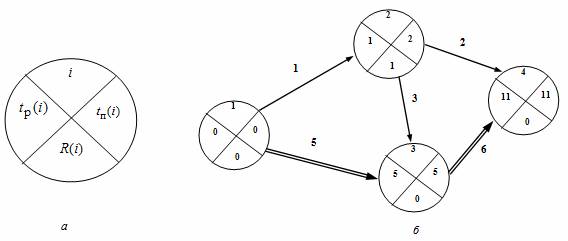
Пример . Определим параметры для событий и критический путь на графике. На практике получил широкое распространение четырехсекторный способ расчета ранних и поздних сроков свершения событий. При этом способе кружок сетевого графика, обозначающий событие, делится на четыре сектора (рис. 2, а). В верхнем ставится номер события i, в левом – наиболее раннее из возможных время свершения события t_p(i), в правом – наиболее позднее из допустимых время свершения события t_п(i), в нижнем – резерв времени данного события R(i).

Рисунок 2 — Графический способ расчета параметров: а) обозначения в вершине графика; б) сетевой график.

Раннее время свершения события t_p(i) определяется продолжительностью максимального пути max(t) до (i), предшествующего событию i: t_p(i)=max(t) до (i).
Послойно, переходя от исходного события до конечного, определим t_p(i). Всегда для начального события t_p(1)=0.
Для события 3 (рис., б) – t_p(3)=max=5; для события 4 – t_p(4)=max=11.
Длина критического пути L_кр=11. Послойно, переходя от конечного события до начального, определим t_п(i). Всегда для конечного события t_п(4)=t(L_кр)=11. Позднее время свершения события t_п(i) определяется временем достаточным для выполнения работ, следующих за этим событием, т.е. зная продолжительность максимального из последующих за событием i путей max(t) после (i) и продолжительность критического пути t(L_кр), можно найти t_п(i)= t(L_кр)-max(t) после (i).
Для события 2 – t_п(3)=11-max=2.
Для критического пути время раннего свершения события t_p(i) равно времени позднего свершения этого события t_п(i), т.е. t_p(i)= t_п(i). Зная ранние и поздние сроки свершения событий сетевого графика, легко выявить резерв времени каждого из них R(i)= t_п(i)- t_p(i).
Резерв времени события показывает максимально допустимое время, на которое можно отодвинуть момент его свершения, не вызывая увеличения критического пути. События критического пути резерва времени не имеют.
Связь параметров сетевого графика для событий и работ показана в таблице.

Таблица — Расчет параметров работ

Время	Начало i → j Окончание
Раннее	tрн(ij)= tp(i)	tро(ij)= tp(i)+tij
Позднее	tпн(ij)= tп(j)-tij	tпо(ij)= tп(j)

Резерв времени для работы R(ij) определяется по формуле: R(ij)= t_п(j)- t_р(i)-t_ij.

Источник