Расчет сетевой модели графическим способом
Сетевой график представляет собой модель процесса возведение отдельного объекта или комплекса объектов с рассчитанными временными параметрами, на которой показана технологическая последовательность выполнения всех работ и их взаимосвязь.
В общих чертах сетевой график может выглядеть следующим образом (рисунок 2):
Рисунок 2 – Сетевая модель
В основу построения сетевого графика положены три понятия: работа, событие, путь.
Работа – производственный процесс, требующий затрат времени и материальных ресурсов и приводящий к достижению определенных результатов. На сетевом графике обозначается сплошными стрелками.
Ожидание – процесс, требующий только затрат времени и не потребляющий никаких материальных ресурсов. Ожидание, в сущности, является технологическим или организационным перерывом между работами, непосредственно выполняемыми друг за другом. На сетевом графике изображается также как работа сплошными стрелками.
Фиктивная работа отражает технологическую взаимосвязь работ и указывает на возможность начала новой работы после завершения предшествующих работ. Фиктивная работа не требует затрат времени и ресурсов, и обозначается в сетевом графике пунктирной стрелкой.
Событие – это факт окончания одной или нескольких работ, необходимых и достаточных для начала следующих работ.
Расчёт сетевой модели данным способом также заключается в определении величины критического пути, ранних и поздних сроков свершения событий, а также резервов времени работ и событий.
Рисунок 3 – Сегмент сетевой модели
Расчет производится в 5 этапов:
— нумерация событий графика;
— расчет ранних начал и заполнение левого и нижнего сектора;
— расчет поздних окончаний и заполнение правого сектора;
— расчет общих (полных) резервов времени работ и заполнение левого прямоугольника под каждой работой;
— расчет частных (свободных) резервов времени и заполнение правого прямоугольника под каждой работой.
При расчёте графическим методом расчётные параметры указываются прямо на сетевой модели (см.рис.2).
Расчёт параметров сетевой модели ведётся в следующей последовательности:
Расчёт ранних сроков (PC) свершения событий:
а) частный случай, для исходного события комплекса принимается равным нулю, t рс исх =0;
б) для остальных событий определяется в строгой последовательности по возрастающим номерам событий.
Для определения PC свершения любого последующего события j рассматриваются все работы, входящие в данное событие. По каждой работе определяется ранний срок свершения конечного события как сумма PC свершения начального события и продолжительности каждой работы. Из полученных значений выбирается максимальное время PC свершения j-гo события:
Данный параметр записывается в левый сектор кружка. Расчет данного параметра (в строгой последовательности по возрастающим номерам событий) выполняется вплоть до завершающего события.
Расчёт поздних сроков (ПС) свершения событий:
а) частный случай, для завершающего события принимаем, что поздний срок этого события строго равен величине раннего срока этого события
б) для остальных событий ПС определяются в обратной последовательности по убывающим номерам событий. Для определения ПС свершения предыдущего события i рассматриваются все работы, выходящие из указанного события. По каждой работе ведется расчет ПС свершения начального события t пс i как разность между ПС свершения конечного события соответствующей работы t пс j и продолжительностью этой работы ti—j.
Из полученных значений выбирается минимальное время ПС свершения i-го события:
Данный параметр записывается в правый сектор кружка.
Продолжительность критического пути определяется по условию:
Резерв времени события определяется по формуле:
Параметр записывается в верхний сектор кружка. Полный резерв времени работы определяется по формуле:
Свободный резерв времени работы определяется по формулам:
Резервы времени соответствующих работ (полный, свободный) записываются под стрелками этих работ. Критический путь проходит через события, имеющие нулевые полный и свободный резервы времени работ и нулевой резерв времени событий.
Результаты расчета сетевой модели графическим способом представлены на рисунке 2. Критический путь имеет такое же значение как при табличном способе расчета.
Графический метод расчета параметров сетевого графика
Рассчитать параметры сетевой модели графическим (секторным) методом можно через калькулятор.
Помимо него существуют следующие способы расчета: табличный метод, метод потенциалов.
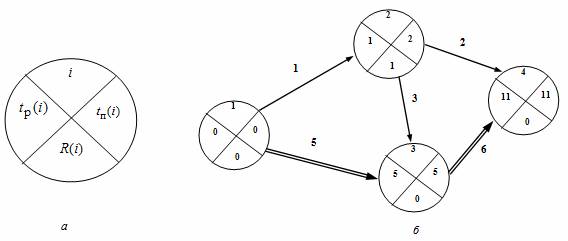
Пример . Определим параметры для событий и критический путь на графике. На практике получил широкое распространение четырехсекторный способ расчета ранних и поздних сроков свершения событий. При этом способе кружок сетевого графика, обозначающий событие, делится на четыре сектора (рис. 2, а). В верхнем ставится номер события i, в левом – наиболее раннее из возможных время свершения события tp(i), в правом – наиболее позднее из допустимых время свершения события tп(i), в нижнем – резерв времени данного события R(i).
Рисунок 2 — Графический способ расчета параметров: а) обозначения в вершине графика; б) сетевой график.
Раннее время свершения события tp(i) определяется продолжительностью максимального пути max(t) до (i), предшествующего событию i: tp(i)=max(t) до (i).
Послойно, переходя от исходного события до конечного, определим tp(i). Всегда для начального события tp(1)=0.
Для события 3 (рис., б) – tp(3)=max=5; для события 4 – tp(4)=max=11.
Длина критического пути Lкр=11. Послойно, переходя от конечного события до начального, определим tп(i). Всегда для конечного события tп(4)=t(Lкр)=11. Позднее время свершения события tп(i) определяется временем достаточным для выполнения работ, следующих за этим событием, т.е. зная продолжительность максимального из последующих за событием i путей max(t) после (i) и продолжительность критического пути t(Lкр), можно найти tп(i)= t(Lкр)-max(t) после (i).
Для события 2 – tп(3)=11-max=2.
Для критического пути время раннего свершения события tp(i) равно времени позднего свершения этого события tп(i), т.е. tp(i)= tп(i). Зная ранние и поздние сроки свершения событий сетевого графика, легко выявить резерв времени каждого из них R(i)= tп(i)- tp(i).
Резерв времени события показывает максимально допустимое время, на которое можно отодвинуть момент его свершения, не вызывая увеличения критического пути. События критического пути резерва времени не имеют.
Связь параметров сетевого графика для событий и работ показана в таблице.
Таблица — Расчет параметров работ
| Время | Начало i → j Окончание | |
| Раннее | tрн(ij)= tp(i) | tро(ij)= tp(i)+tij |
| Позднее | tпн(ij)= tп(j)-tij | tпо(ij)= tп(j) |
Резерв времени для работы R(ij) определяется по формуле: R(ij)= tп(j)- tр(i)-tij.
1.3.2. Графический метод
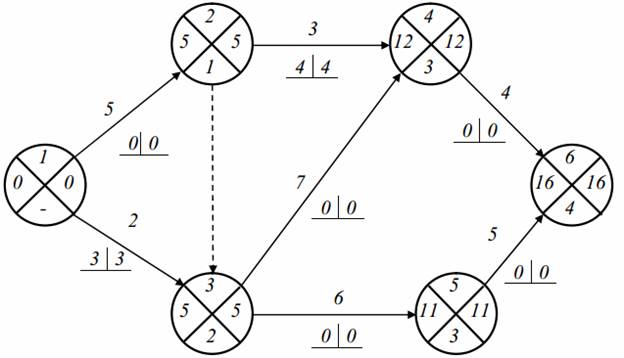
Данный метод предусматривает расчет параметров непосредственно на сетевом графике. Для этого все кружки (события) делятся на 4 сектора (рис. 17). В нижних секторах проставляются коды событий; в левых секторах в процессе расчета записываются ранние сроки свершения событий (tpi); в правых – поздние сроки свершения событий (tпi); в верхних секторах – резервы свершения событий (Pi).
Рис. 17. Пример расчета сети графическим способом
Расчет ранних сроков свершения событийведется слева направо, начиная с исходного события, и заканчивается завершающим событием. При этом ранний срок свершения исходного события принимается равным нулю (tpi= 0).
Ранний срок свершения j-го события определяется по формуле (1). Если в j-е событие входит одна работа, то tpj= tpi+tij(например, для события №2 tp2 = 0 + 2 = 2). Если j-му событию предшествует несколько работ, тоtpj = max(tpi + tij). Например, для события №5 максимальное значение равно 8 (tp5= макс (tp3 + t3-5; tp2 + t2-5; tp4 + t4-5) = (8 + 0; 4 + 2; 2 + 3 = 8).
Таким образом, расчет ведется до завершающего события. Ранний срок свершения последнего события определяет продолжительность критического пути и срок выполнения всего комплекса работ.
Расчет поздних сроков свершения событийведется справа налево, начиная с завершающего события и заканчивается исходным.
Поздний срок свершения завершающего события совпадает с ранним сроком его свершения. Например, tп6 = tр6 = 12 (рис. 17). Это значение записывается в правом секторе завершающего события.
Поздний срок свершения i-го события определяется по формуле (2) . Это значение записывается в правом секторе i-го события. Если из i-го события выходит несколько работ, то выбирается минимальное значение. Например, для события №3минимальное значение равно 8 (tp3= мин (tp6 — t3-6; tp5 + t3-5) = (12 – 4; 10 – 0 = 8)) (рис. 17).
Таким образом, расчет ведется до исходного события.
Резервы времени на свершение событийопределяются по формуле(3)и записываются в верхний сектор события (кружка).
После расчета ранних и поздних сроков свершения событий по формулам (8)и(9)рассчитываются полные и свободные резервы работ. Полученные значения записываются в квадратных скобках возле обозначения и продолжительности работы (см.рис. 17).
Все события, которые не имеют резервов времени (Pi = 0), лежат на критическом пути. Однако если работа соединяет два события не имеющих резервов это не обязательно свидетельствует о том, что она относится к критическому пути. Однозначным свидетельством принадлежности работы к критическому пути является отсутствие у нее полного резерва.
В рассматриваемом примере (рис. 17) критический путь проходит через работы«а»—«в»—«з». Его длительность составляет 12 (3 +5 +4), что совпадает с ранним сроком последнего события.
1.3.3. Табличный метод
Для расчета параметров сетевого графика этим методом составляется таблица, число строк в которой соответствует числу работ. Таблица включает в себя следующие столбцы: