1. Основные понятия сетевой модели
Сетевая модель — графическое изображение плана выполнения комплекса работ, состоящего из нитей (работ) и узлов (событий), которые отражают логическую взаимосвязь всех операций. В основе сетевого моделирования лежит изображение планируемого комплекса работ в виде графа.
Граф — схема, состоящая из заданных точек (вершин), соединенных линиями. Отрезки, соединяющие вершины, называются ребрами (дугами) графа.
Ориентированным называется такой граф, на котором стрелкой указаны направления всех его ребер, что позволяет определить, какая из двух его граничных вершин является начальной, а какая — конечной. Исследование таких сетей проводится методами теории графов.
Теория графов оперирует понятием пути, объединяющим последовательность взаимосвязанных ребер. Контур означает такой путь, у которого начальная вершина совпадает с конечной. Сетевой график — это ориентированный граф без контуров. В сетевом моделировании имеются два основных элемента — работа и событие.
Работа — это активный процесс, требующий затрат ресурсов, либо пассивный (ожидание), приводящий к достижению намеченного результата.
Фиктивная работа — это связь между результатами работ (событиями), не требующая затрат времени и ресурсов.
Событие — это результат (промежуточный или конечный) выполнения одной или нескольких предшествующих работ.
Путь — это любая непрерывная последовательность (цель) работ и событий.
Критический путь — это путь, не имеющий резервов и включающий самые напряженные работы комплекса. Работы, расположенные на критическом пути, называют критическими. Все остальные работы являются некритическими (ненапряженными) и обладают резервами времени, которые позволяют передвигать сроки их выполнения, не влияя на общую продолжительность выполнения всего комплекса работ.
При построении сетевых моделей необходимо соблюдать следующие правила.
- Сеть изображается слева направо, и каждое событие с большим порядковым номером изображается правее предыдущего. Общее направление стрелок, изображающих работы, также в основном должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером.
- Два соседних события могут объединяться лишь одной работой. Для изображения параллельных работ вводятся промежуточное событие и фиктивная работа (рис. 27-1).
- В сети не должно быть тупиков, т.е. промежуточных событий, из которых не выходит ни одна работа (рис. 27.2).
- В сети не должно быть промежуточных событий, которым не предшествует хотя бы одна работа (рис. 27.3).
- В сети не должно быть замкнутых контуров, состоящих из взаимосвязанных работ, создающих замкнутую цепь (рис. 27.4).
Для правильной нумерации событий поступают следующим образом: нумерация событий начинается с исходного события, которому дается номер 1. Из исходного события 1 вычеркивают все исходящие из него работы, на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию дается номер 2. Затем вычеркивают работы, выходящие из события 2, и вновь находят на оставшейся части сети событие, в которое не входит ни одна работа, ему присваивается номер 3, и так продолжается до завершающего события. Продолжительность выполнения работ устанавливается на сновании действующих нормативов или по экспертным оценкам специалистов. В первом случае временные оценки являются детерминированными (однозначными), во втором — стохастическими (вероятностными).
Расчет сетевой модели графическим способом
Сетевой график представляет собой модель процесса возведение отдельного объекта или комплекса объектов с рассчитанными временными параметрами, на которой показана технологическая последовательность выполнения всех работ и их взаимосвязь.
В общих чертах сетевой график может выглядеть следующим образом (рисунок 2):
Рисунок 2 – Сетевая модель
В основу построения сетевого графика положены три понятия: работа, событие, путь.
Работа – производственный процесс, требующий затрат времени и материальных ресурсов и приводящий к достижению определенных результатов. На сетевом графике обозначается сплошными стрелками.
Ожидание – процесс, требующий только затрат времени и не потребляющий никаких материальных ресурсов. Ожидание, в сущности, является технологическим или организационным перерывом между работами, непосредственно выполняемыми друг за другом. На сетевом графике изображается также как работа сплошными стрелками.
Фиктивная работа отражает технологическую взаимосвязь работ и указывает на возможность начала новой работы после завершения предшествующих работ. Фиктивная работа не требует затрат времени и ресурсов, и обозначается в сетевом графике пунктирной стрелкой.
Событие – это факт окончания одной или нескольких работ, необходимых и достаточных для начала следующих работ.
Расчёт сетевой модели данным способом также заключается в определении величины критического пути, ранних и поздних сроков свершения событий, а также резервов времени работ и событий.
Рисунок 3 – Сегмент сетевой модели
Расчет производится в 5 этапов:
— нумерация событий графика;
— расчет ранних начал и заполнение левого и нижнего сектора;
— расчет поздних окончаний и заполнение правого сектора;
— расчет общих (полных) резервов времени работ и заполнение левого прямоугольника под каждой работой;
— расчет частных (свободных) резервов времени и заполнение правого прямоугольника под каждой работой.
При расчёте графическим методом расчётные параметры указываются прямо на сетевой модели (см.рис.2).
Расчёт параметров сетевой модели ведётся в следующей последовательности:
Расчёт ранних сроков (PC) свершения событий:
а) частный случай, для исходного события комплекса принимается равным нулю, t рс исх =0;
б) для остальных событий определяется в строгой последовательности по возрастающим номерам событий.
Для определения PC свершения любого последующего события j рассматриваются все работы, входящие в данное событие. По каждой работе определяется ранний срок свершения конечного события как сумма PC свершения начального события и продолжительности каждой работы. Из полученных значений выбирается максимальное время PC свершения j-гo события:
Данный параметр записывается в левый сектор кружка. Расчет данного параметра (в строгой последовательности по возрастающим номерам событий) выполняется вплоть до завершающего события.
Расчёт поздних сроков (ПС) свершения событий:
а) частный случай, для завершающего события принимаем, что поздний срок этого события строго равен величине раннего срока этого события
б) для остальных событий ПС определяются в обратной последовательности по убывающим номерам событий. Для определения ПС свершения предыдущего события i рассматриваются все работы, выходящие из указанного события. По каждой работе ведется расчет ПС свершения начального события t пс i как разность между ПС свершения конечного события соответствующей работы t пс j и продолжительностью этой работы ti—j.
Из полученных значений выбирается минимальное время ПС свершения i-го события:
Данный параметр записывается в правый сектор кружка.
Продолжительность критического пути определяется по условию:
Резерв времени события определяется по формуле:
Параметр записывается в верхний сектор кружка. Полный резерв времени работы определяется по формуле:
Свободный резерв времени работы определяется по формулам:
Резервы времени соответствующих работ (полный, свободный) записываются под стрелками этих работ. Критический путь проходит через события, имеющие нулевые полный и свободный резервы времени работ и нулевой резерв времени событий.
Результаты расчета сетевой модели графическим способом представлены на рисунке 2. Критический путь имеет такое же значение как при табличном способе расчета.
Сетевая модель данных
В сетевой структуре при тех же основных понятиях (уровень, узел, связь) каждый элемент может быть связан с любым другим элементом. На рис. 3 изображена сетевая структура базы данных в виде графа.
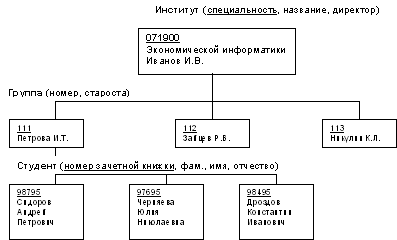
Пример. Примером сложной сетевой структуры может служить структура базы данных, содержащей сведения о студентах, участвующих в научно-исследовательских работах (НИРС). Возможно участие одного студента в нескольких НИРС, а также участие нескольких студентов в разработке одной НИРС. Графическое изображение описанной в примере сетевой структуры, состоящей только из двух типов записей, показано на рис. 4. Единственное отношение представляет собой сложную связь между записями в обоих направлениях.
Рис. 2. Пример иерархической структуры БД
Р Рис. 3. Графическое изображение сетевой структурыЕляционная модель данных
Понятие реляционный (англ. relation — отношение) связано с разработками известного американского специалиста в области систем баз данных Е. Кодда.
Эти модели характеризуются простотой структуры данных, удобным для пользователя табличным представлением и возможностью использования формального аппарата алгебры отношений и реляционного исчисления для обработки данных.
Реляционная модель ориентирована на организацию данных в виде двумерных таблиц. Каждая реляционная таблица представляет собой двумерный массив и обладает следующими свойствами:
- каждый элемент таблицы – один элемент данных;
- все столбцы в таблице однородные, т.е. все элементы в столбце имеют одинаковый тип (числовой, символьный и т.д.) и длину;
- каждый столбец имеет уникальное имя;
- одинаковые строки в таблице отсутствуют;
- порядок следования строк и столбцов может быть произвольным.
Пример. Реляционной таблицей можно представить информацию о студентах, обучающихся в вузе (Рис. 4).
| № л/д | Фамилия | Имя | Отчество | Дата рождения | Группа |
| 16493 | Сергеев | Петр | Михайлович | 01.01.76 | 111 |
| 16593 | Петрова | Анна | Владимировна | 15.03.75 | 112 |
| 16693 | Анохин | Андрей | Борисович | 14.04.76 | 111 |
Рис. 4. Пример реляционной таблицы Отношения представлены в виде таблиц, строки которых соответствуют кортежам или записям, а столбцы — атрибутам отношений, доменам, полям. Поле, каждое значение которого однозначно определяет соответствующую запись, называется простым ключом (ключевым полем). Если записи однозначно определяются значениями нескольких полей, то такая таблица базы данных имеет составной ключ. В примере, показанном на Рис. 4, ключевым полем таблицы является «№ личного дела». Чтобы связать две реляционные таблицы, необходимо ключ первой таблицы ввести в состав ключа второй таблицы (возможно совпадение ключей); в противном случае нужно ввести в структуру первой таблицы внешний ключ — ключ второй таблицы. Пример. На рис. 5 показан пример реляционной модели, построенной на основе отношений: СТУДЕНТЫ, СЕССИЯ, ПРЕДМЕТЫ. СТУДЕНТЫ(Код студента, Фамилия, Имя, Пол, Дата рождения, Телефон, Группа). СЕССИЯ(Код студента, Код предмета, Оценка). ПРЕДМЕТЫ(Код предмета, Название, Преподаватель). Таблица СЕССИЯ имеет два внешних ключа Код студентаиКод предмета, которые обеспечивают ее связь с таблицами СТУДЕНТЫ и ПРЕДМЕТЫ.