Теоретические основы проектного управления
Для описания, анализа и оптимизации проектов наиболее подходящими оказались сетевые модели.
В сетевой модели роль вершин графа могут играть события, определяющие начало и окончание отдельных работ, а дуги в этом случае будут соответствовать работам. Такую сетевую модель принято называть сетевой моделью с работами на дугах (Activities on Arrows, AoA). В то же время, возможно, что в сетевой модели роль вершин графа играют работы, а дуги отображают соответствие между окончанием одной работы и началом другой. Такую сетевую модель принято называть сетевой моделью с работами в узлах (Activities on Nodes, AoN).
Пусть множество A= – комплекс работ, выполнение которых требуется для решения определенной задачи, например, строительства дома. Тогда, если множество V= будет представлять комплекс событий, возникающих в процессе выполнения комплекса работ, то сетевая модель будет задаваться ориентированным графом G=(V, A), в котором элементы множества V играют роль вершин, а элементы множества A – роль дуг, соединяющих вершины, причем каждой дуге ai можно поставить в однозначное соответствие пару вершин (vsi, vfi), первая из которых будет определять момент начала работы аi, а вторая – момент окончания этой работы. Такая сетевая модель будет сетевой моделью с работами на дугах.
Теперь пусть множество A= – по-прежнему будет рассматриваться как комплекс работ, выполнение которых требуется для решения определенной задачи, например, строительства дома. Тогда, если множество V= будет представлять комплекс отношений предшествования-следования работ в процессе их выполнения, то сетевая модель будет задаваться ориентированным графом G=(A, V), в котором элементы множества A играют роль вершин, а элементы множества V – роль дуг, соединяющих вершины, причем каждой дуге vi можно поставить в однозначное соответствие пару вершин (asi, afi), первая из которых будет непосредственно предшествующей работой в данной паре, а вторая – непосредственно следующей. Такая сетевая модель будет сетевой моделью с работами в узлах.
Сетевая модель может быть представлена: 1) сетевым графиком, 2) в табличной форме, 3) в матричной форме, 4) в форме диаграммы на шкале времени. Как будет показано ниже, переход от одной формы представления к другой не составляет большого труда.
Преимущество сетевых графиков и временных диаграмм перед табличной и матричной формами представления состоит в их наглядности. Однако это преимущество исчезает прямо пропорционально тому, как увеличиваются размеры сетевой модели. Для реальных задач сетевого моделирования, в которых речь идет о тысячах работ и событий, вычерчивание сетевых графиков и диаграмм теряет всякий смысл.
Преимущество табличной и матричной формы перед графическими представлениями состоит в том, что с их помощью удобно осуществлять анализ параметров сетевых моделей; в этих формах применимы алгоритмические процедуры анализа, выполнение которых не требует наглядного отображения модели на плоскости.
Сетевым графиком называется полное графическое отображение структуры сетевой модели на плоскости.
Если сетевым графиком на плоскости отображается сетевая модель типа АоА, то однозначное представление должны получить все работы и все события модели. Однако структура сетевого графика модели АоА может быть более избыточна, чем структура самой отображаемой сетевой модели. Дело в том, что по правилам построения сетевого графика для удобства его анализа необходимо, чтобы два события были соединены только единственной работой, что в принципе не соответствует реальным обстоятельствам в окружающей нас действительности. Поэтому принято вводить в структуру сетевого графика элемент, которого нет ни в действительности, ни в сетевой модели. Этот элемент называется фиктивной работой. Таким образом, структура сетевого графика образуется из трех типов элементов (в отличие от структуры сетевой модели, где только два типа элементов):
- событий – моментов времени, когда происходит начало или окончание выполнения какой-либо работы (работ);
- работ – неделимых частей комплекса действий, необходимых для решения некоторой задачи;
- фиктивных работ – условных элементов структуры сетевого графика, используемых исключительно для указания логической связи отдельных событий.
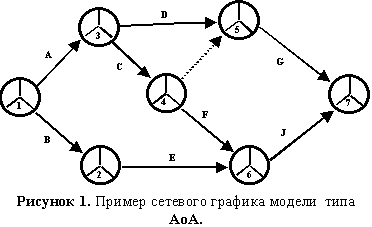
Графически события изображаются кружками, разделенными на три равных сегмента (радиусами под углом в 120°); работы изображаются сплошными линиями со стрелками на конце, ориентированными слева направо; фиктивные работы изображаются пунктирными линиями со стрелками на конце, ориентированными слева направо. Пример сетевого графика модели АоА представлен ниже на рис. 1.
Отметим, что индексация работ производится рядом с соответствующими стрелками; фиктивные работы не индексируются; индексы событий проставляются в нижнем сегменте соответствующего кружка. Заполнение остальных сегментов рассматривается ниже.
Если сетевым графиком отображается модель типа AoN, то избыточности структуры удается избежать. Здесь нет необходимости вводить в качестве дополнительного структурного элемента фиктивные работы, поскольку отсутствуют те структурные элементы, которые они призваны обслуживать, а именно – события. В сетевом графике модели типа AoN есть только узлы (или вершины), которые обозначают работы и дуги (сплошные линии со стрелками, ориентированными слева направо), которые обозначают отношения предшествования-следования работ. Никаких событий и никаких фиктивных работ! Заметим, что в наиболее известной программе по проектному управлению Microsoft Project реализуется именно этот тип модели.
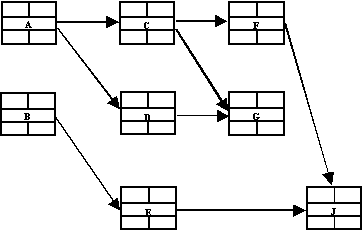
Здесь узлы сети, соответствующие работам, принято изображать прямоугольниками, поделенными на 5 секторов. В центральном секторе проставляется индекс (или записывается наименование работы). Заполнение остальных секторов рассматривается ниже. Пример сетевого графика для модели типа AoN представлен ниже на рис. 2.
Рисунок 2. Пример сетевого графика модели типа АоN.
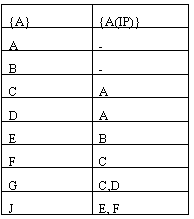
В табличной форме сетевая модель задается множеством , где А – это множество индексов работ, а A(IP) множество комбинаций работ, непосредственно предшествующих работе А. Для рассматриваемого выше примера табличная форма сетевой модели будет такой, которая представлена в табл. 1.
Таблица 1. Табличная форма сетевой модели.
Матричная форма описания сетевой модели задается в виде отношения между событиями (ei, ej), которое равно 1, если между этими событиями есть работа (либо реальная, либо фиктивная) и 0 – в противном случае. Матричная форма для описания сетевой модели из рассматриваемого выше примера приведена ниже в табл. 2:
График Ганта и сетевые матрицы
Другим инструментом анализа является график Ганта — диаграмма, изображающая задания в виде отрезков на временной шкале. Длина отрезка соответствует сроку задания. Весь проект представляется в форме календаря, что позволяет использовать его для контроля и показа процента выполнения задания.
Разновидностью графика Ганта являются сетевые матрицы,для составления которых определяются следующие характеристики (табл.57):
· состав и содержание отдельных работ по проекту;
· последовательность выполнения работ с учетом максимально возможного запараллеливания работ;
· исполнители каждой работы.
Таблица 57 — Перечень работ для построения сетевой матрицы
| № предшеству- ющей работы | № данной работы | Содержание данной работы | Ориентировочная продолжитель-ность, дн. | Исполнитель |
Сетевая матрица представляет собой графическое изображение процессов осуществления проекта, где все работы (управленческие, производственные и т.д.) показаны в определенной технологической последовательности и взаимосвязи. Сетевая матрица совмещается с календарно-масштабной сеткой времени которая имеет горизонтальные и вертикальные “коридоры”. Горизонтальные “коридоры” характеризуют степень управления, структурное подразделение или должностное лицо, выполняющее ту или иную работу; вертикальные — этап и отдельные операции процесса управления проектом, протекающие во времени. При построении сетевой матрицы используются три основных понятия: «работа» (включая ожидание и зависимость), «событие» и «путь».
На графике работа изображается в виде сплошной стрелки. В понятие “работа” включается процесс ожидания, т.е. процесс, требующий затрат не труда и ресурсов, а времени, который изображается пунктирной стрелкой с обозначением над ней продолжительности ожидания. Зависимость между событиями указывает на наличие связи между работами и на отсутствие необходимости в затратах времени и ресурсов.
Важнейшим преимуществом сетевой матрицы является то, что отпадает необходимость производить расчеты параметров матриц, так как они наглядно показаны на самом рисунке (см. рис. 29).
| Подраз-деления | Код работ | Продолжи-тельность (дн.) | Численность персонала | Д н и |
| в под-разделе-нии, чел. | Занятого на рабо-те, чел. | … | ||
| Отдел главного технолога | 0-1 | |||
| 1-3 | ||||
| 0-8 | ||||
| Отдел главного конструкт. | 1-2 | |||
| 4-5 | ||||
| 8-9 | ||||
| ОГМ | 0-4 | |||
| ПО | 0-10 | |||
| Цех по изготовл. оснастки | 2-3 | |||
| 5-6 | ||||
| 9-10 | ||||
| Цех механообр. | 7-10 | |||
| 3-10 | ||||
| Цех литейн. | 6-7 | |||
| Цех сбороч. | 10-11 |
Рисунок 29 — Пример сетевой матрицы (фрагмент)
Сетевые матрицы должны использоваться на всех стадиях жизненного цикла проекта. Это позволит представить весь процесс осуществления проекта в наглядной форме, а также выявить состав и структуру работ и приемлемые средства и методы их выполнения, проанализировать взаимосвязи между исполнителями и работой, подготовить научно обоснованный скоординированный план выполнения всего комплекса работ по проекту для более эффективного использования имеющихся ресурсов и сокращения сроков. Представляется также возможность быстро обрабатывать большие массивы информации, прогнозировать ход выполнения работ на критическом пути и концентрировать на них внимание менеджеров проекта. Используя математический аппарат, можно определять степень вероятности реализации проекта и правильно распределить ответственность.
Дата добавления: 2020-10-25 ; просмотров: 291 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ