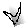Как построить сетевую модель пример

Пример построения сетевого графика

Используя полученные данные, мы можем найти основные характеристики сетевой модели табличным методом, критический путь и его продолжительность.
Таблица – Табличный метод расчета сетевого графика.

КПР	Код работы (i,j)	Продолжительность работы t(i, j)	Ранние сроки		Поздние сроки		Резервы времени
			tрн(i,j)	tро(i,j)	tпн(i,j)	tпо(i,j)	Rп	Rc
1	2	3	4	5	6	7	8	9
0	1,2	7	0	7	0	7	0	0
0	1,4	4	0	4	17	21	17	8
0	1,5	3	0	3	19	22	19	0
1	2,3	3	7	10	7	10	0	0
1	2,8	13	7	20	19	32	12	12
1	3,4	2	10	12	19	21	9	0
1	3,6	13	10	23	10	23	0	0
2	4,7	5	12	17	21	26	9	0
1	5,7	4	3	7	22	26	19	10
1	6,8	9	23	32	23	32	0	0
2	7,8	6	17	23	26	32	9	9

Таким образом, работы критического пути (1,2),(2,3),(3,6),(6,8). Продолжительность критического пути Т_кр=32.

Рисунок — Масштабный график сетевой модели
Для оценки вероятности выполнения всего комплекса работ за 30 дней нам необходима следующая формула: P(t_кр где Z=(Т-Т_кр)/S_кр
Z- нормативное отклонение случайной величины, S_кр – среднеквадратическое отклонение, вычисляемое как корень квадратный из дисперсии продолжительности критического пути. Соответствие между Z и Ф(Z) представлено в таблице.
Таблица — Таблица стандартного нормального распределения.

Z	F(Z)	Z	F(Z)	Z	F(Z)
0	0.0000	1.0	0.6827	2.0	0.9643
0.1	0.0797	1.1	0.7287	2.1	0.9722
0.2	0.1585	1.2	0.7699	2.2	0.9786
0.3	0.2358	1.3	0.8064	2.3	0.9836
0.4	0.3108	1.4	0.8385	2.4	0.9876
0.5	0.3829	1.5	0.8664	2.5	0.9907
0.6	0.4515	1.6	0.8904	2.6	0.9931
0.7	0.5161	1.7	0.9104	2.7	0.9949
0.8	0.5763	1.8	0.9281	2.8	0.9963
0.9	0.6319	1.9	0.9545	2.9	0.9973

Критический путь проходит по работам (1,2)(2,3)(3,6)(3,8).
Дисперсия критического пути:
S 2 ­(L_кр)= S 2 (1,2)+ S 2 (2,3)+ S 2 (3,6)+S 2 (6,8)=1+0,25+4+1=6,25
S(L_кр)=2,5
p(t_кр<30)=0,5+0,5Ф((30-32)/2,5)=0,5-0,5Ф(0,8) = 0,5-0,5*0,5763=0,5-0,28815=0,213
Вероятность того, что весь комплекс работ будет выполнен не более чем за 30 дней, составляет 21,3%.
Для определения максимально возможного срока выполнения всего комплекса работ с надежностью 95% будем использовать следующую формулу: T=Т_кр+Z*S_кр Для решения поставленной задачи найдем значение аргумента Z, которое соответствует заданной вероятности 95% (значению графы Ф(Z) 0,9545*100% в таблице 5 соответствует Z=1,9).
T=32+1,9*2,5=36,8
Максимальный срок выполнения всего комплекса работ при заданном уровне вероятности 95% составляет всего 36,8 дня.

Источник

1.3.5. Пример построения и расчета сетевой модели

Исходные данные варианта лабораторной работы включают название и продолжительность каждой работы (табл. 1.1), а также описание упорядочения работ.

1. Работы C, I, Gявляются исходными работами проекта, которые могут выполняться одновременно.
2. Работы E иAследуют за работойC.
3. Работа Hследует за работойI.
4. Работы D иJследуют за работойG.
5. Работа Bследует за работойE.
6. Работа Kследует за работамиAиD, но не может начаться прежде, чем не завершится работаH.
7. Работа Fследует за работойJ.

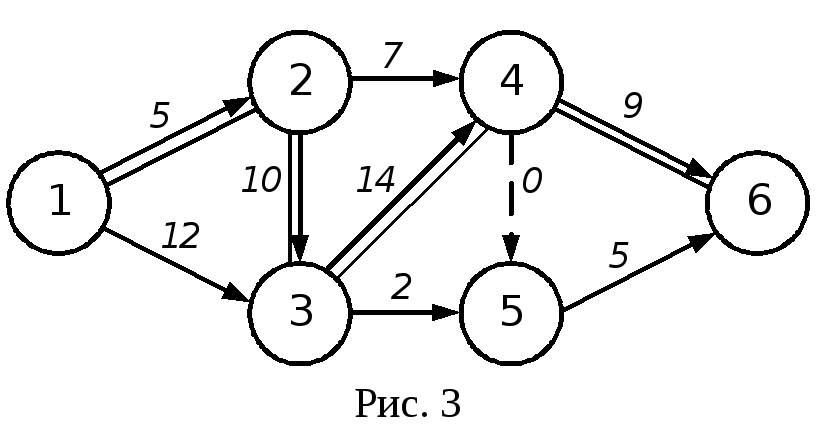
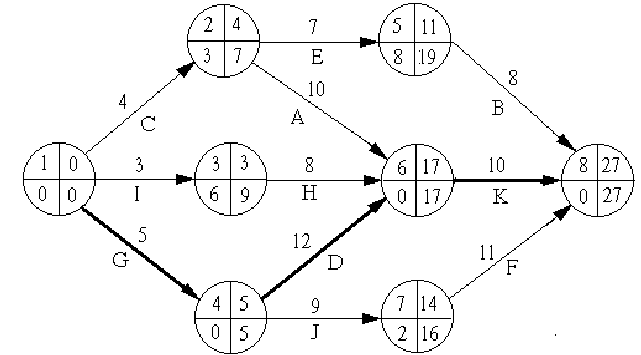
На рис.1.4 представлена сетевая модель, соответствующая данному упорядочению работ. Каждому событию присвоен номер, что позволяет в дальнейшем использовать не названия работ, а их коды (см. табл. 1.2). Численные значения временных параметров событий сети вписаны в соответствующие секторы вершин сетевого графика, а временные параметры работ сети представлены в табл. 1.3. Таблица 1.2 Описание сетевой модели с помощью кодирования работ

Номера событий		Код работы	Продолжительность
начального	конечного	работы
1	2	(1,2)	4
1	3	(1,3)	3
1	4	(1,4)	5
2	5	(2,5)	7
2	6	(2,6)	10
3	6	(3,6)	8
4	6	(4,6)	12
4	7	(4,7)	9
5	8	(5,8)	8
6	8	(6,8)	10
7	8	(7,8)	11

Рис.1.4. Сетевая модель Таблица 1.3 Временные параметры работ

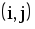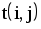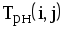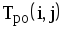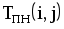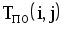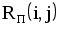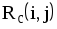1,2	4	0	4	3	7	3	0
1,3	3	0	3	6	9	6	0
1,4	5	0	5	0	5	0	0
2,5	7	4	11	12	19	8	0
2,6	10	4	14	7	17	3	3
3,6	8	3	11	9	17	6	6
4,6	12	5	17	5	17	0	0
4,7	9	5	14	7	16	2	0
5,8	8	11	19	19	27	8	8
6,8	10	17	27	17	27	0	0
7,8	11	14	25	16	27	2	2

1.4. Контрольные вопросы

1.4.1. Зачетный минимум

1. Определение события, виды событий, практические примеры событий, обозначение событий на графике, временные параметры событий.
2. Определение работы, классификация работ с приведением соответствующих практических примеров, обозначение работ на графике, временные параметры работ.
3. Правила построения сетевых графиков.
4. Определение пути в сетевом графике, виды путей, важность определения критического пути.
5. Умение вычислять временные параметры событий и работ.

1.4.2. Дополнительные вопросы

1. Почему при расчете раннего срока свершения события iвыбираютмаксимальнуюиз сумм ?
2. Почему при расчете позднего срока свершения события iвыбираютминимальнуюиз разностей ?
3. Какова взаимосвязь полного и свободного резервов работы?
4. Как можно найти критических путь в сетевой модели, без непосредственного суммирования длительностей работ?

Часть 2. ОПТИМИЗАЦИЯ СЕТЕВЫХ МОДЕЛЕЙ ПО КРИТЕРИЮ «МИНИМУМ ИСПОЛНИТЕЛЕЙ» 2.1. ЦЕЛЬ РАБОТЫ Знакомство с методикой и приобретение навыков проведения оптимизации сетевых моделей по критерию «Минимум исполнителей». 2.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Согласно номеру своего варианта получите данные о количество исполнителей, занятых на каждой работе сетевой модели, и ограничение по численности Nодновременно занятых в работе исполнителей. 2. Постройте в отчете графики привязки и загрузки, используя нормальные длительности работ сети — 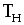(см. п.2.3.1), и покажите их преподавателю. 3. Проверьте правильность построения графиков привязки и загрузки с помощью компьютера, в случае необходимости выявите и устраните ошибки. 4. Используя компьютерную программу, проведите уменьшение численности исполнителей, одновременно занятых на работах сети, до требуемого уровня N. 5. Отчет по лабораторной работе должен содержать:

• номер варианта;
• исходные данные варианта;
• графики привязки и загрузки до проведения оптимизации загрузки;
• графики привязки и загрузки после проведения оптимизации загрузки (возможно использование пунктирных линий на первоначально построенных графиках для отображение изменений в привязке работ и загрузке сети, вызванных сдвигами работ);
• коды работ, сдвинутых в процессе оптимизации, и время их сдвига.

Источник

1. Элементы построения сетевых моделей

В основе метода сетевого планирования и управления (СПУ) лежит построение графика, по своему виду напоминающего сеть (переплетение нитей и узелков), поэтому график и получил название сетевого.

Сетевой моделью называется отображение процессов, выполнение которых подчинено достижению одной или нескольких целей, с указанием взаимосвязей между этими процессами.

Сетевым графиком называется график производства работ с установленными расчётом сроками их выполнения. Сетевой график представляет собой графическое изображение сетевой модели с рассчитанными параметрами.

Элементами сетевой модели являются работа, событие и путь:

а) работа – это трудовой процесс, требующий затрат времени и ресурсов.

Название работы является минимальной информацией о работе, содержащейся в сетевой модели (например, отрывка котлована, возведение каркаса, устройство кровли, поставка оборудования и т.д.).

Работа на графике изображается сплошной стрелкой, направленной слева направо с указанием над стрелкой продолжительности работы.

Работа, которая требует лишь затрат времени, называется работа – ожидание. Ожидание на графике изображается пунктирной стрелкой с указанием над стрелкой её продолжительности (например, процесс твердения бетона или ожидание поставки материалов). Эти работы требуют только затрат времени.

Для отображения правильной технологической последовательности между работами применяется зависимость. Ни времени, ни ресурсов «зависимость» не требует. На графике зависимость изображают пунктирной стрелкой, продолжительность которой равна нулю. В литературных источниках зависимость называют фиктивной работой.

Итак, понятие «работа» может иметь три значения:

работа

работа – ожидание

зависимость

б) событие – это итог какой-нибудь деятельности (работы), происходящей мгновенно. Любая работа начинается и заканчивается событием.

Событие не потребляет ни времени, ни трудовых ресурсов, оно обозначает только факт начала и окончания одной или нескольких работ. Событие графически обозначается кружком, внутри которого ставится его номер, или может обозначаться буквами.

Событие, не имеющее непосредственно предшествующих работ, называется исходным, не имеющее непосредственно следующих работ – завершающим. Событие, не являющееся ни исходным, ни завершающим, называется промежуточным.

На рис. 1 событие 1 – исходное, событие 6 – завершающее, события 2, 3, 4, 5 – промежуточные.

Все работы комплекса по отношению друг к другу подразделяются на данную, предшест-вующую и последующую работы. Обозначение работ см. на рис. 2.

в) путь – это непрерывная технологическая последовательность работ от исходного события к завершающему.

На рис. 3 дан сетевой график из восьми работ, одной зависимости и шести событий. На графике можно выделить 7 путей:

1-й путь проходит по событиям 1, 2, 3, 4, 6;

2-й путь проходит по событиям 1, 3, 5, 6;

3-й путь проходит по событиям 1, 2, 4, 6;

4-й путь проходит по событиям 1, 2, 3, 5, 6;

5-й путь проходит по событиям 1, 2, 3, 4, 5, 6;

6-й путь проходит по событиям 1, 2, 4, 5, 6;

7-й путь проходит по событиям 1, 3, 4, 5, 6.

Зная продолжительность каждой работы t_ij , можно определить продолжительность любого пути сетевого графика.

Продолжительность пути определяется как сумма продолжительностей работ, составляющих этот путь:

Критический путь – это путь, имеющий максимальную продолжительность. Он определяет конечный срок строительства, это самый трудоемкий и неблагоприятный путь.

Подкритический путь – это путь, продолжительность которого близка к продолжительности критического пути.

На рис. 3 длина различных путей от исходного события до завершающего равна:

1-й путь Т₁ = 5 + 10 + 14 + 9 = 38;

4-й путь Т₄ = 5 + 10 + 2 + 3 = 20;

5-й путь Т₅ = 5 + 10 + 0 + 3 = 32;

6-й путь Т₆ = 5 + 7 + 0 + 3 = 15;

7-й путь Т₇ = 12 + 14 + 0 + 3 = 29.

Первый путь имеет наибольшую продолжительность из всех путей, значит, он является критическим.

Критическим путь назван потому, что, во-первых, из всех путей сетевого графика только он определяет общую продолжительность строительства; во-вторых, он указывает на работы, которые являются ведущими для выполнения заданного комплекса работ. Работы, лежащие на критическом пути, называются критическими.

На рис. 3 критическими работами являются 1-2; 2-3; 3-4; 4-6.

На сетевом графике критический путь выделяют красной двойной или жирной линией.

В сетевом графике может быть несколько критических путей одинаковой продолжительности. Определение продолжительности (длины) критического пути и критических работ – одна из основных задач, решаемых в методе сетевого планирования и управления (СПУ).

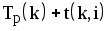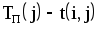Источник