Построение сетевой модели
Целесообразность применения сетей различных типов определяется в каждом конкретном случае особенностями комплекса и характером решаемых задач планирования и управления. Хотя построение сетей типа «работы-вершины» проще, однозначно и не требует введения дополнительных элементов (фиктивных работ), во многих случаях предпочитают сети типа «работы-дуги», поскольку в последних отражены события комплекса. Кроме того, при большом числе входящих и выходящих работ сеть типа «работы-дуги» оказывается более экономной (по числу элементов).
Рассмотрим правила построения сети типа «работы-дуги». Для построения сетевого графика приняты определенные условные изображения и обозначения работ, их результатов и связей между ними.
По своему содержанию и изображению в сетевом графике работа подразделяется (рис.1.3.) на:
ü работу, требующую затрат времени и труда (изображается на графике сплошной линией со стрелкой);
ü фиктивную работу (или связь, зависимость),не требующую затрат времени и труда; показывающую логическую связь между событиями и одновременно указывающую, что возможность начала одной работы зависит от результата другой работы (изображается на графике штриховой линией со стрелкой);
ü ожидание, или работу, требующую затрат времени, но не требующую затрат труда (изображается на графике сплошной линией со стрелкой).
Рис.1.3.Изображение работ в сетевом графике
По очередности выполнения все работы, изображенные в сетевом графике, могут быть подразделены на последовательные и параллельные. Последовательной называется работа, которая может быть начата только после окончания другой, ей предшествующей. Параллельными называются работы, которые могут выполняться одновременно после наступления события, обусловливающего возможность их начала.
При построении сетевого графика могут возникнуть ошибки, некоторые из которых обнаруживаются формальными приемами анализа сетевого графика.
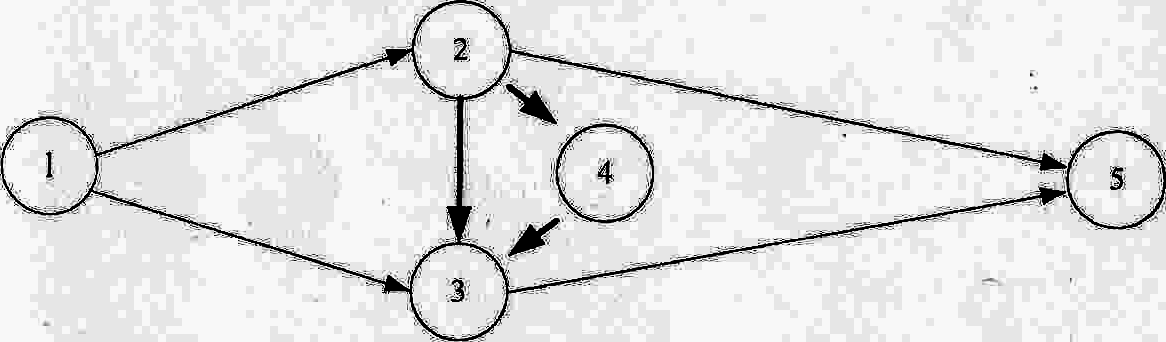
В частности, признаками ошибок, допущенных при построении сети, являются циклы (контуры) и тупики (рис.1.4.)
Из ошибок, для обнаружения которых можно указать формальные правила, наиболее распространены следующие:
наличие событий, не являющихся исходными событиями и не имеющих входящих работ (тупики первого рода –событие B на рис.1.4.);
наличие событий, не являющихся завершающими (целевыми) событиями и не имеющих исходящих работ (тупики второго рода – событие А на рис.1.4.);
наличие замкнутых путей-контуров (1-2-3-1 на рис.1.4.)
Рис.1.4.Пример сети с тупиками и контурами
Ошибки типа неправильно указанного номера события не противоречат основным правилам построения сетей (если они не приводят к появлению тупиков и контуров), поэтому для них нельзя построить формальные правила обнаружения, и они могут быть устранены только путем тщательного просмотра исходных данных модели.
Наличие контура свидетельствует об искажении отношений порядка между работами, входящими в цикл (контур), поскольку каждая из этих работ оказывается предшествующей самой себе и любой другой из работ, образующих цикл, чего не может быть в реальности.
Тупики в сети могут появиться, например, в результате того, что:
ü в исходной информации о сети пропущены некоторые работы;
ü в сеть внесены события и работы, которые не являются необходимыми для достижения целей моделируемого комплекса.
Все ошибки (тупики и контуры) должны быть устранены.
Таким образом, сетевая модель будет иметь следующий вид (рис.1.5.)
Таким образом, можно сформулировать основные свойства работ и событий сетевой модели:
1. Событию непосредственно предшествует, по крайней мере, одна работа и, по крайней мере, одна следует за ним (за исключением исходного и завершающего).
2. Ко всем работам, имеющим своим началом некоторое событие, можно приступить только тогда, когда окончены все непосредственно предшествующие ему (событию) работы.
Рассмотрим пример составления сетевой модели.
У фирмы Х появился конкурент. Для сохранения своих позиций на рынке сбыта администрация фирмы Х приняла решение о скорейшем внедрении в производство конкурентоспособной продукции и поручила менеджеру составить план разработки нового товара и внедрения его на потребительский рынок.
Перечень необходимых задач, которые необходимо решить для этого, их взаимосвязь и время даны в таблице 1.1. Составить сетевой граф.
Таблица 1.1.Исходные данные
| Задачи | Время, недель | Предшествующие задачи |
| А. Создание новой продукции | — | |
| В. Создание упаковки | — | |
| С. Подготовка производственной мощности | А | |
| D. Получение сырья и материалов | А | |
| E. Выпуск опытной партии продукции | C,D | |
| F. Упаковка | B | |
| G. Принятие решения о выборе пробного рынка сбыта | — | |
| H. Упаковка опытной партии | E,F | |
| I. Поставка продукции на пробный рынок сбыта | H,G | |
| J. Продажа продукции на пробном рынке сбыта | I | |
| K. Оценка результатов внедрения продукции на рынок | J | |
| L. Планирование выпуска продукции на национальном уровне | K |
Рис.1.6.Сетевая модель типа «работа-вершина»
Рис.1.7.Сетевая модель типа «работа-дуга»
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Расчёт сетевого графика «вершины-работы»
Для расчёта сетевого графика «вершины-работы» прямоугольник, изображающий работу, делят на 7 частей (рис. 6.6). В верхних трёх частях прямоугольника записываются раннее начало, продолжительность и раннее окончание работы, в трёх нижних позднее начало, резервы времени и позднее окончание. Центральная часть содержит код (номер) и наименование работы.
Расчёт сетевого графика начинается с определения ранних сроков. Ранние начала и окончания вычисляются последовательно от исходной до завершающей работы. Раннее начало исходной работы равно 0, раннее окончание – сумме раннего начала и продолжительности работы:
Например, для работы (1): t po 1 = t p н 1 + t1 = 0 + 2 = 2.
Код и наименование работы
Рис. 6.6. Работа в сетевом графике «вершины-работы»
Раннее начало последующей работы равно раннему окончанию предыдущей работы. Если данной работе непосредственно предшествуют несколько работ, то её раннее начало будет равно максимальному из ранних окончаний предшествующих работ:
Таким образом, определяются ранние сроки всех работ сетевого графика и заносятся в верхние правую и левую части.
Раннее окончание завершающей работы определяет продолжительность критического пути.
Расчёт поздних сроков ведется в обратном порядке от завершающей до исходной работы. Позднее окончание завершающей работы равно её раннему окончанию, т.е. продолжительности критического пути: t по 10 = 20
Позднее начало определяется как разность позднего окончания и продолжительности:
Например, для работы (10): t пн 10 = t по 10 = t10 — 20 — 1 = 19. Позднее начало последующих работ становится поздним окончанием предшествующих работ. Если за данной работой непосредственно следуют несколько работ, то её позднее окончание будет равно минимальному из поздних начал последующих работ:
Подобным образом определяются поздние сроки всех работ сетевого графика и записываются в левую и правую нижние части.
Полный резерв времени, равный разности поздних и ранних сроков, заносится в числитель середины нижней части:
R = t пн — t PH = t по — t ро
R3 = t пн 3 — t рн 3= 4 — 2 = 2 = t по 3 — t po 3 = 7 — 5 = 2
Свободный резерв времени, равный разности между минимальным ранним началом последующих работ и ранним окончанием данной работы, записывается в знаменатель середины нижней части:
Свободный резерв всегда меньше или равен полному резерву работы.
Пример расчёта сетевого графика «вершины — работы» приведен на рис. 6.7
Рис. 6.7. Пример расчета сетевого графика «вершины-работы»
Последовательность работ с нулевыми резервами времени является критическим путём сетевого графика. В данном примере работы 1, 2, 5, 9, 10 находятся на критическом пути, продолжительность которого равна Ткр = 20.
Правила построения сетевых графиков
Для построения сетевого графика необходимо выявить последовательность и взаимосвязь работ: какие работы необходимо выполнить, и какие условия обеспечить, чтобы можно было начать данную работу, какие работы можно и целесообразно выполнять параллельно с данной работой, какие работы можно начать после окончания данной работы. Эти вопросы позволяют выявить технологическую взаимосвязь между отдельными работами, обеспечивают логическое построение сетевого графика и его соответствие моделируемому комплексу работ.
Уровень детализации сетевого графика зависит от сложности строящегося объекта, количества используемых ресурсов, объёмов работ и продолжительности строительства.
Имеется два типа сетевых графиков:
Сетевые графики типа «вершины — работы».
Элементами такого графика являются работы и зависимости. Работа представляет собой определенный производственный процесс, требующий затрат времени и ресурсов для его выполнения, и изображается прямоугольником. Зависимость (фиктивная работа) показывает организационно-технологическую связь между работами, не требующую затрат времени и ресурсов, изображается стрелкой. Если между работами имеется организационный или технологический перерыв, то на зависимости указывается длительность этого перерыва. Пример сетевого графика «вершины — работы» приведен на рис. 6.1.
Рис. 6.1. Сетевой график типа «вершины — работы»
Если работа сетевого графика «вершины — работы» не имеет предшествующих работ, то она является исходной работой этого графика. Если работа не имеет последующих работ, то она является завершающей работой сетевого графика. В сетевом графике «вершины — работы» не должно быть замкнутых контуров (циклов), т.е. зависимости не должны возвращаться в ту работу, из которой они вышли.
Сетевые графики типа «вершины-события».
Элементами такого типа графиков являются работы, зависимости и события. Работа изображается сплошной стрелкой, зависимость – пунктирной. Событие представляет собой результат одной или нескольких работ, необходимый и достаточный для начала одной или нескольких последующих работ, и изображается кружком.
В сетевых графиках этого типа каждая работа находится между двумя событиями: начальным, из которого она выходит, и конечным, в которое она входит. События сетевого графика нумеруются, поэтому каждая работа имеет код, состоящий из номеров её начального и конечного события. Например, на рис. 6.2 работы закодированы как (1,2); (2,3); (2,4); (4,5).
Рис.6.2. Сетевой график «вершины — события»
Если событие сетевого графика «вершины-события» не имеет предшествующих работ, то оно является исходным событием этого графика. Следующие непосредственно за ним работы называются исходными. Если событие не имеет последующих работ, то оно является завершающим событием. Входящие в него работы называются завершающими.
Для правильного отображения взаимосвязей между работами необходимо соблюдать следующие основные правила построения сетевого графика «вершины-события»:
1. При изображении одновременно или параллельно выполняемых работ (например, работ «Б» и «В» на рис.6.2) вводятся зависимость (3,4) и дополнительное событие (3).
2. Если для начала работы «Г» необходимо выполнить работы «А» и «Б», а для начала работы «В» – только работу «А», то вводится зависимость и дополнительное событие (рис.6.3.).
Рис.6.3. Изображение зависимости между работами
3. В сетевом графике не д.б. замкнутых контуров (циклов), т.е. цепочки работ, возвращающейся к тому событию, из которого они вышли (рис.6.4).
Рис. 6.4. Пример замкнутого контура (2,4,3,2)
4. В сетевом графике при поточной организации строительства вводятся дополнительные события и зависимости (рис. 6.5.).
Рис. 6 5. Пример изображения потоков однородных работ