Как создавать сетевую модель

Тонкости построения сетевых моделей в Python

Что является основным инструментом, который использует руководитель при управлении проектом? Принято считать, что основным инструментом руководителя проекта является календарный план, в основе которого лежит сетевая модель работ по проекту. Однажды мне довелось реализовать сетевую модель работ на языке Python (код и описание здесь). Ниже приведены уроки, извлеченные по результатам проделанной работы.

Сначала создай работы, потом устанавливай связи

При построении сетевой модели часто возникает вопрос, в каком порядке создавать работы и устанавливать связи между ними? Наиболее очевидным является двухэтапный подход – сначала создаются все работы модели, затем между ними устанавливаются связи. Такой подход позволяет избежать ошибок типа KeyError: ‘101’, возникающих при параллельном выполнении этих двух операций, когда система пытается установить связь с работой, которая еще не была создана.

Конечно, суммарное время выполнения двух последовательных операций по созданию работ и установке связей между ними может быть оптимизировано за счет использования алгоритма, в котором эти операции выполняются параллельно. Однако даже на больших моделях с десятком тысяч работ последовательные алгоритмы работают достаточно быстро. Поэтому в условиях временных ограничений на реализацию проекта вполне можно обойтись классическим двухэтапным подходом.

Пересчитывай модель после её построения

Стоит ли выполнять пересчет всякий раз, когда происходит установка связи между работами при построении сетевой модели? С одной стороны, постоянный пересчет позволяет держать модель в актуальном состоянии. С другой, пересчет увеличивает время ее построения.

Для сравнения были реализованы две функции:

1. build_model_by_method() – построение с пересчетом модели;
2. build_model_by_assignment() – построение без пересчета модели.

from predict import Activity import xml.etree.ElementTree as ET import sys import timeit from timeit import Timer # вычисляем значение параметра задачи def get_child(child, activity_field): text = child.find(activity_field).text if text is None: return None return int(text) # строим модель с использованием метода пересчета def build_model_by_method(filename): sys.setrecursionlimit(10000) f = open(filename,'r') tree = ET.parse(f) root = tree.getroot() schedule = <> next = <> for child in root.findall('Activity'): start_date = get_child(child,'start_date') finish_date = get_child(child,'finish_date') duration = get_child(child,'duration') not_early_date = get_child(child,'not_early_date') a = Activity(id, start_date, finish_date, duration, not_early_date) schedule[id] = a next_activity = '' if child.find('next_activity').text is None else child.find('next_activity').text next[id] = next_activity for key in schedule: if nextКак создавать сетевую модель != '': for next_id in nextКак создавать сетевую модель.split(';'): scheduleКак создавать сетевую модель.append_next(schedule[next_id]) sys.setrecursionlimit(1000) # строим модель без использования метода пересчета def build_model_by_assignment(filename): f = open(filename,'r') tree = ET.parse(f) root = tree.getroot() schedule = <> next = <> for child in root.findall('Activity'): start_date = get_child(child,'start_date') finish_date = get_child(child,'finish_date') duration = get_child(child,'duration') not_early_date = get_child(child,'not_early_date') a = Activity(id, start_date, finish_date, duration, not_early_date) schedule[id] = a next_activity = '' if child.find('next_activity').text is None else child.find('next_activity').text next[id] = next_activity for key in schedule: if nextКак создавать сетевую модель != '': for next_id in nextКак создавать сетевую модель.split(';'): scheduleКак создавать сетевую модель.next_activity.append(schedule[next_id]) # считаем скорость построения модели print('Test for 100 activities:') t1 = Timer("build_model_by_method('data/activity_100.xml')", "from __main__ import build_model_by_method") print("build_model_by_method", t1.timeit(number = 1000)) t2 = Timer("build_model_by_assignment('data/activity_100.xml')", "from __main__ import build_model_by_assignment") print("build_model_by_assignment", t2.timeit(number = 1000)) print('Test for 1000 activities') t3 = Timer("build_model_by_method('data/activity_1000.xml')", "from __main__ import build_model_by_method") print("build_model_by_method", t3.timeit(number = 1000)) t4 = Timer("build_model_by_assignment('data/activity_1000.xml')", "from __main__ import build_model_by_assignment") print("build_model_by_assignment", t4.timeit(number = 1000)) print('Test for 10000 activities') t5 = Timer("build_model_by_method('data/activity_10000.xml')", "from __main__ import build_model_by_method") print("build_model_by_method", t5.timeit(number = 1000)) t6 = Timer("build_model_by_assignment('data/activity_10000.xml')", "from __main__ import build_model_by_assignment") print("build_model_by_assignment", t6.timeit(number = 1000)) 

$ python network.py Test for 100 activities: build_model_by_method 1.7820062519999738 build_model_by_assignment 1.426311435999878 Test for 1000 activities build_model_by_method 18.998158786999966 build_model_by_assignment 14.216093206999858 Test for 10000 activities build_model_by_method 249.93449528199994 build_model_by_assignment 148.85600239800033 

Как видно, чем больше работ, тем медленнее работает функция построения сетевой модели с использованием пересчета по сравнению с функцией, в которой пересчет не используется.

Контролируй глубину рекурсии

Сетевая модель проекта состоит из работ и связей между ними. В отсутствии дополнительной информации о сети для ее пересчета используются рекурсивные алгоритмы. Такие алгоритмы состоят в последовательном проходе по работам сети и пересчете их параметров (например, длительности, дат начала и окончания). Чем больше работ в сети, тем больше глубина рекурсии.

Известно, что в Python по умолчанию установлено ограничение на глубину рекурсии – не больше 1000 рекурсивных вызовов. Для получения этого ограничения предназначен метод getrecursionlimit() модуля sys.

>>> import sys >>> sys.getrecursionlimit() 1000

При работе с большими сетями, число работ в которых измеряется десятками тысяч, обычной ситуацией является превышение глубины рекурсии и, как следствие, возникновение ошибки типа RecursionError: maximum recursion depth exceeded in comparison. Ошибка приводит к остановке построения либо пересчета модели и падению системы.

Чтобы предотвратить ошибку, построить и пересчитать большую сеть, необходимо увеличить ограничение на глубину рекурсии. И в этом нам поможет метод setrecursionlimit() модуля sys.

 >>> import sys >>> sys.setrecursionlimit(10000) >>> sys.getrecursionlimit() 10000

До какого значения требуется увеличить глубину рекурсии? Ответ на этот вопрос зависит от структуры сетевой модели. Если структура неизвестна или достаточно сложна, рекомендую устанавливать ограничение в значение, равное количеству работ в сети. Рекурсивный алгоритм проходится либо по всем либо по части работ. Поэтому глубина рекурсии не должна превысить количество работ в сети.

И напоследок…

Управление проектами – это модно. Но модно еще не значит эффективно. На рынке существуют программные решения по пересчету сетевых моделей, такие как Microsoft Project. Однако алгоритмы, зашитые в них остаются доступными только вендерам соответствующего программного обеспечения.

Настоящая статья написана на основе опыта разработки открытого модуля по построению и пересчету сетевых моделей проектов. Я надеюсь, что приведенные в статье извлеченные уроки будут полезны читателю как с теоретической, так и с чисто практической точки зрения. Если настоящая статья вызовет интерес, то я поделюсь новыми знаниями, которые возникнут в дальнейшем, по мере развития модуля.

Источник

Анализ сетевого графика

Созданный сетевой график можно сохранить в форматах docx и png (меню Действия ). Далее можно найти параметры сетевой модели (критический путь, резервы времени, построить диаграмму Ганта и многое другое).

Инструкция к сервису

Для добавления вершины на графическое полотно необходимо использовать соответствующую фигуре кнопку Добавить . Новый объект также можно вставить, предварительно выделив его левой кнопкой мыши, а затем щелкнуть мышкой на рабочем поле. Нумерация вершин может начинаться с 0 , для этого нужно снять отметку с пункта Нумерация вершин с №1 .

Чтобы соединить вершины, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить .
Сетевая модель может быть представлена в табличной форме и в виде матрицы весов (матрицы расстояний). Чтобы использовать данные представления, выберите меню Операции .

Построенный граф можно сохранить в формате docx или png .
Если в качестве формы вершин используется прямоугольник, то при построении секторальной диаграммы применяется методология Microsoft Visio с отображением параметров duration, ES, EF, LS, LF, and slack.

Основные определения

• «действительная работа» – процесс, требующий затрат времени и ресурсов;
• «фиктивная работа» – логическая связь между двумя или несколькими работами, указывающая на то, что начало одной работы зависит от результатов другой. Фиктивная работа не требует затрат времени и ресурсов, продолжительность ее равна нулю.

Правила построения сетевой модели

• в сети не должно быть «тупиков», т.е., событий, от которых не начинается ни одна работа, исключая завершающее событие графика;
• В сетевом графике не должно быть «хвостовых» событий, то есть событий, которым не предшествует хотя бы одна работа, за исключением исходного.
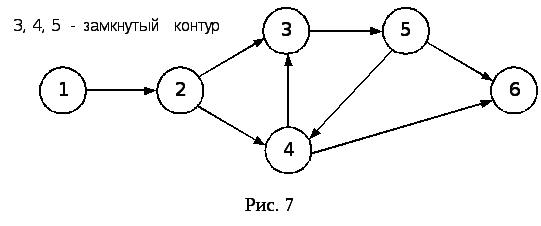
• в сети не должно быть замкнутых контуров (рис.1);
• Любые два события должны быть непосредственно связаны не более чем одной работой.
• В сети рекомендуется иметь одно исходное и одно завершающее событие.
• Сетевой график должен быть упорядочен. То есть события и работы должны располагаться так, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.

Методы оптимизации сетевого графика

Логико-математическое описание, формирование планов и управляющих воздействий осуществляется на базе использования особого класса моделей, называемых сетевыми моделями.
После построения и расчета сетевого графика (определения его параметров), выполнения анализа графика, заключающегося в оценке его целесообразности и структуры, оценке загрузки исполнителей, оценке вероятности наступления завершающего события в заданный срок, следует приступать к оптимизации сетевого графика. Процедура оптимизации заключается в приведение графика в соответствие с заданными сроками выполнения работ, возможностями подрядных организаций и т.д. В общем случае под оптимизацией следует понимать процесс улучшения организации выполнения работ.

• Оптимизация сетевой модели по критерию «число исполнителей». Заполняется столбец Количество исполнителей Ч ►
• Оптимизация сетевой модели по критерию «время – стоимость» ( время — затраты ). В случае известных коэффициентов затрат на ускорение работ заполняется только этот столбец h(i,j) . Иначе, заполняются столбцы t_опт (Нормальный режим), Минимальное время работ, t_min (Ускоренный режим), Нормальная стоимость, Cн и Срочная стоимость, Cc .

Источник

2. Правила построения сетевых моделей

В сетевой модели должна отражаться технологическая последовательность и очерёдность отдельных работ. Модель должна иметь простую форму. Стрелки должны быть направлены слева направо от события с меньшим номером к событию с большим номером, необходимо стремиться к минимальному пересечению отдельных работ.

2.1. Основные правила

1. Правило составных работ – любая работа а может быть разбита на составляющие, если после частичного выполнения её можно начать следующую работу б. При этом вводятся логические зависимости и дополнительные события (рис. 4).

2. Правило параллельных работ – если между двумя событиями необходимо показать две или несколько работ, которые выполняются параллельно, в модели вводятся дополнительное событие по окончании одной из параллельных работ и логическая зависимость (фиктивная работа) между ними (рис. 5).

3. Правило зависимых и независимых работ – если для начала одной работыг необходимо выполнение всех пред-шествующих работ a и б, а для начала работы в необходимо выполнение только работы a, то вводятся дополнительное событие и логическая зависимость (рис. 6).

4. Правило запрещения замкнутых контуров, т.е. один путь не должен дважды проходить через одно событие (рис. 7).

5. Правило запрещения тупиковых событий, т.е. событий, из которых не выходит ни одна работа, если событие не завершающее (рис. 8).

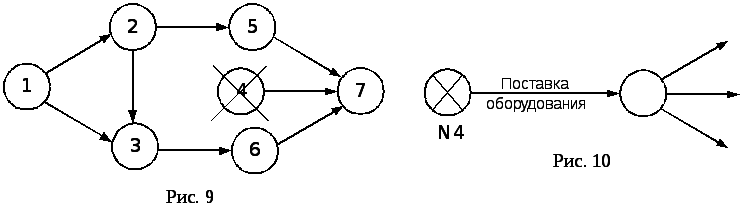
6. Правило запрещения необеспеченных событий, т.е. со- бытий, в которые не входит ни одна работа, если событие не исходное (рис. 9).

7. Правило изображения поставки (рис. 10).

2.2. Построение сетей

Для построения сетевой модели нужно знать технологию работ и зависимость одних работ от других. Последовательность выполнения работ записывается в форме таблицы, в которой указывается зависимость данной работы ig от предшествующей hi.

Пример 1. По данной зависимости работ построить сетевую модель.

Источник