УПОРЯДОЧЕНИЕ СЕТЕВОГО ГРАФИКА
Сетевой моделью называется план выполнения некоторого комплекса работ, который отражает логическую взаимосвязь всех операций. В основе сетевого моделирования лежит изображение планируемого комплекса работ в виде сетевого графа..
Основными элементами сетевой модели являются события и работы.
Термин работа в СПУ имеет следующий смысл:
1) действительная работа – активный процесс, требующий затрат ресурсов;
2) ожидание – временной процесс, не требующий затрат труда;
3) фиктивная работа (зависимость) – это логическая связь между двумя или несколькими работами, указывающая, что возможность выполнения одной работы непосредственно зависит от результата другой работы.
Событие – это момент завершения какого–либо процесса (работы). Оно обладает свойствами:
1) Может свершиться только после того, как закончится все предшествующие ему работы.
2) Все последующие работы могут начаться только после того, как данное событие свершится.
Таким образом, событие является конечным для всех предшествующих ему работ и начальным – для всех непосредственно следующих за ним работ.
Если событие не имеет предшествующих работ, то оно называется исходным, а если не имеет последующих работ – завершающим или конечным.
События на сетевом графике (или графе) изображаем кружками (вершинами графа), а работы — стрелками (ориентированными дугами), которые показывают связь между событиями. Рассмотрим пример сетевого графика (рис. 1), состоящего из 12 событий и 24 работ, связывающих их.
События 0,1,…,11; работы: (0,1), (0,2), (0,3),…, (10,11).
Это пример структурной сети, так как в модели отсутствуют числовые оценки работ. В дальнейшем будем рассматривать сети, в которых заданы оценки работ (продолжительность, стоимость и т.д.).
ПОРЯДОК И ПРАВИЛА ПОСТРОЕНИЯ СЕТЕВЫХ ГРАФИКОВ
Сетевые графики составляются на начальном этапе планирования.
Порядок построения
1) Планируемый процесс разбивается на отдельные работы, составляется перечень работ и событий, продумываются последовательность выполнения работ и логические связи между ними, оценивается «стоимость» работ. Другими словами, строится календарный график, определяющий начало и окончание каждой операции, а также взаимосвязи с другими операциями графика.
2) Составляется (сшивается) сетевой график (см. рис.1).
3) Производится упорядочение сетевого графика, рассчитываются параметры событий и работ, определяются резервы времени и критический путь.
4) Проводится анализ и оптимизация сетевого графика.
Правила построения
1) В сетевой модели не должно быть «тупиковых» событий, из которых не выходит ни одна работа, за исключением завершающего события.
2) В сетевой модели не должно быть «хвостовых» событий, которым не предшествует хотя бы одна работа, за исключением исходного.
3) В сети не должно быть замкнутых контуров или петель, то есть путей, которые соединяют событие с самим собой.
4) Любые два события могут быть связаны не более чем одной работой.
5) В сети рекомендуется иметь одно исходное и одно завершающее событие.
Если эти правила (или часть из них) в сети не выполняются, то необходимо более тщательное изучение процесса и определение «пропущенных» работ, или введение фиктивных работ.
Кроме того, фиктивные работы вводят в модель для отражения реальных отсрочек и ожидания, и здесь фиктивная работа будет характеризоваться определенной продолжительностью во времени.
УПОРЯДОЧЕНИЕ СЕТЕВОГО ГРАФИКА
Сетевой график изображенный на рис.1, отвечает правилам §2, но он не полностью упорядочен.
Упорядочением сетевого графика называется такое расположение событий и работ, при котором для любой работы предшествующее ей событие расположено левее и имеет меньший номер, по сравнению с событием, завершающим эту работу.
То есть все «стрелки-работы» направлены слева направо от событий с меньшими номерами к событиям с большими номерами.
Упорядочим наш сетевой график, расположив все стрелки слева направо, а события — в 9-ти вертикальных слоях.
Теперь перенумеруем события в соответствии с их расположением на вертикальных слоях и поставим в соответствие каждой работе число — продолжительность работ. Продолжительность выполнения работ устанавливается на основании действующих нормативов или согласно экспертных оценок специалистов. В первом случае временные оценки являются детерминированными (однозначными), во втором – стохастическими (вероятностными). При этом нумерацию событий в одном слое проведем сверху-вниз (это не принципиально).
2. Правила построения сетевых моделей
В сетевой модели должна отражаться технологическая последовательность и очерёдность отдельных работ. Модель должна иметь простую форму. Стрелки должны быть направлены слева направо от события с меньшим номером к событию с большим номером, необходимо стремиться к минимальному пересечению отдельных работ.
2.1. Основные правила
1. Правило составных работ – любая работа а может быть разбита на составляющие, если после частичного выполнения её можно начать следующую работу б. При этом вводятся логические зависимости и дополнительные события (рис. 4).
2. Правило параллельных работ – если между двумя событиями необходимо показать две или несколько работ, которые выполняются параллельно, в модели вводятся дополнительное событие по окончании одной из параллельных работ и логическая зависимость (фиктивная работа) между ними (рис. 5).
3. Правило зависимых и независимых работ – если для начала одной работыг необходимо выполнение всех пред-шествующих работ a и б, а для начала работы в необходимо выполнение только работы a, то вводятся дополнительное событие и логическая зависимость (рис. 6).
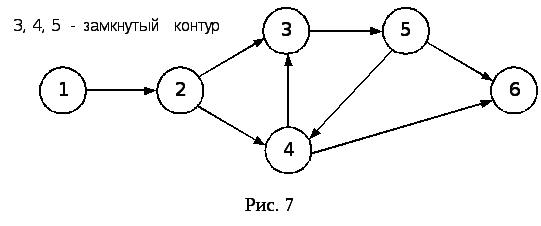
4. Правило запрещения замкнутых контуров, т.е. один путь не должен дважды проходить через одно событие (рис. 7).
5. Правило запрещения тупиковых событий, т.е. событий, из которых не выходит ни одна работа, если событие не завершающее (рис. 8).
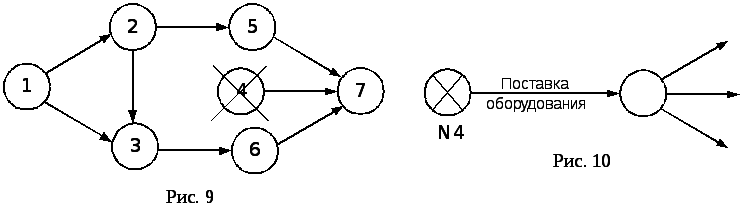
6. Правило запрещения необеспеченных событий, т.е. со- бытий, в которые не входит ни одна работа, если событие не исходное (рис. 9).
7. Правило изображения поставки (рис. 10).
2.2. Построение сетей
Для построения сетевой модели нужно знать технологию работ и зависимость одних работ от других. Последовательность выполнения работ записывается в форме таблицы, в которой указывается зависимость данной работы ig от предшествующей hi.
Пример 1. По данной зависимости работ построить сетевую модель.
Упорядочение сетевой модели
Планирование проектов с учетом временных параметров
Временные параметры сетевой модели
Для выполнения работы требуются ресурсы и время. Время, необходимое для выполнения работы (i , j), будем называть продолжительностьюработы и обозначать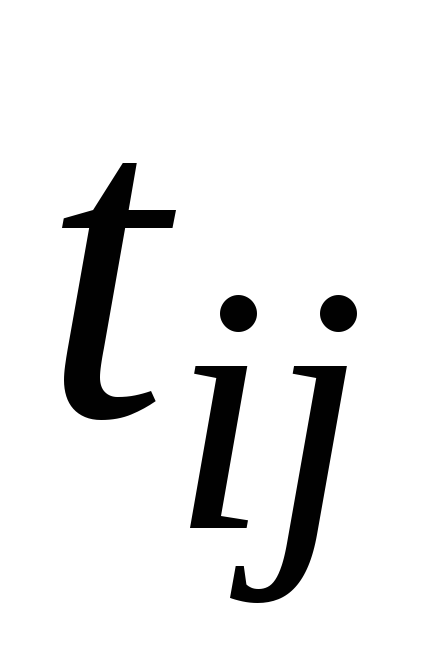 
. Продолжительность выполнения работы непосредственно связана с ресурсами, необходимыми для выполнения работы. Чем больше ресурсов отпущено на выполнение работы, тем меньше ее продолжительность. Если при выполнении какого-либо проекта ресурсы практически не ограничены (приоритетные задания), то имеют место так называемые системы СПУ без учета ресурсов. Расчет продолжительности выполнения работ для моделей этой группы ведется оценочными методами без увязки с имеющимися ресурсами и особой трудности не представляет. Как правило, все планируемые комплексы работ функционируют в условиях ограниченных ресурсов, что связывает процесс определения продолжительности работ с задачами распределения ресурсов. Продолжительность выполнения работы 
(3.1) где 
— объем работы (i,j) по ресурсу вида k;
— коэффициент использования ресурса вида k на работе (i,j); 
— количество ресурса вида k, используемого для выполнения работы (i,j) в единицу времени. Характеристики объема работы и коэффициента использования ресурсов могут быть как нормативными и определяться из справочников по нормативам, так и назначаться на основе экспертных оценок руководителем проекта. Количество ресурсов, используемых на работах, может быть как расчетным показателем, получаемым по результатам решения задач распределения ресурсов, так и оценочной величиной, назначаемой руководителем проекта. Кроме продолжительности выполнения работы к временным параметрам сетевой модели относятся: момент начала выполнения комплекса работ — минимальный из моментов начала работ комплекса; момент завершения комплекса — максимальный из моментов окончания работ комплекса; продолжительность выполнения комплекса работ — промежуток времени между моментами начала и завершения комплекса; продолжительность пути — сумма продолжительностей выполнения всех работ пути; директивные сроки — верхние ограничения моментов свершения целевых или контрольных событий.
Для продолжения скачивания необходимо пройти капчу: