Классификация нейронных сетей по топологии

Классификация нейронных сетей

Нейронная сеть представляет собой совокупность нейронов, определенным образом соединенных друг с другом и с внешней средой с помощью связей, определяемых ве­совыми коэффициентами. В зависимости от функций, выполняе­мых нейронами в сети, можно выделить три их типа:

• входные нейроны, на которые подается вектор, кодирую­щий входное воздействие или образ внешней среды; в них обычно не осуществляется вычислительных процедур, а информация пе­редается с входа на выход;

• выходные нейроны, выходные значения которых пред­ставляют выходы нейронной сети;

• промежуточные нейроны, составляющие основу нейрон­ных сетей.

В большинстве нейронных моделей тип нейрона связан с его расположением в сети. Если нейрон имеет только выходные связи, то это входной нейрон, если наоборот — выходной нейрон. Однако возможен случай, когда выход топологически внутреннего нейрона рассматривается как часть выхода сети. В процессе функциониро­вания сети осуществляется преобразование входного вектора в выходной, некоторая переработка информации. Конкретный вид выполняемого сетью преобразования данных обусловливается не только характеристиками нейроподобных элементов, но и особен­ностями ее архитектуры, а именно топологией межнейронных свя­зей, выбором определенных подмножеств нейроподобных элемен­тов для ввода и вывода информации, способами обучения сети, наличием или отсутствием конкуренции между нейронами, на­правлением и способами управления и синхронизации передачи информации между нейронами.

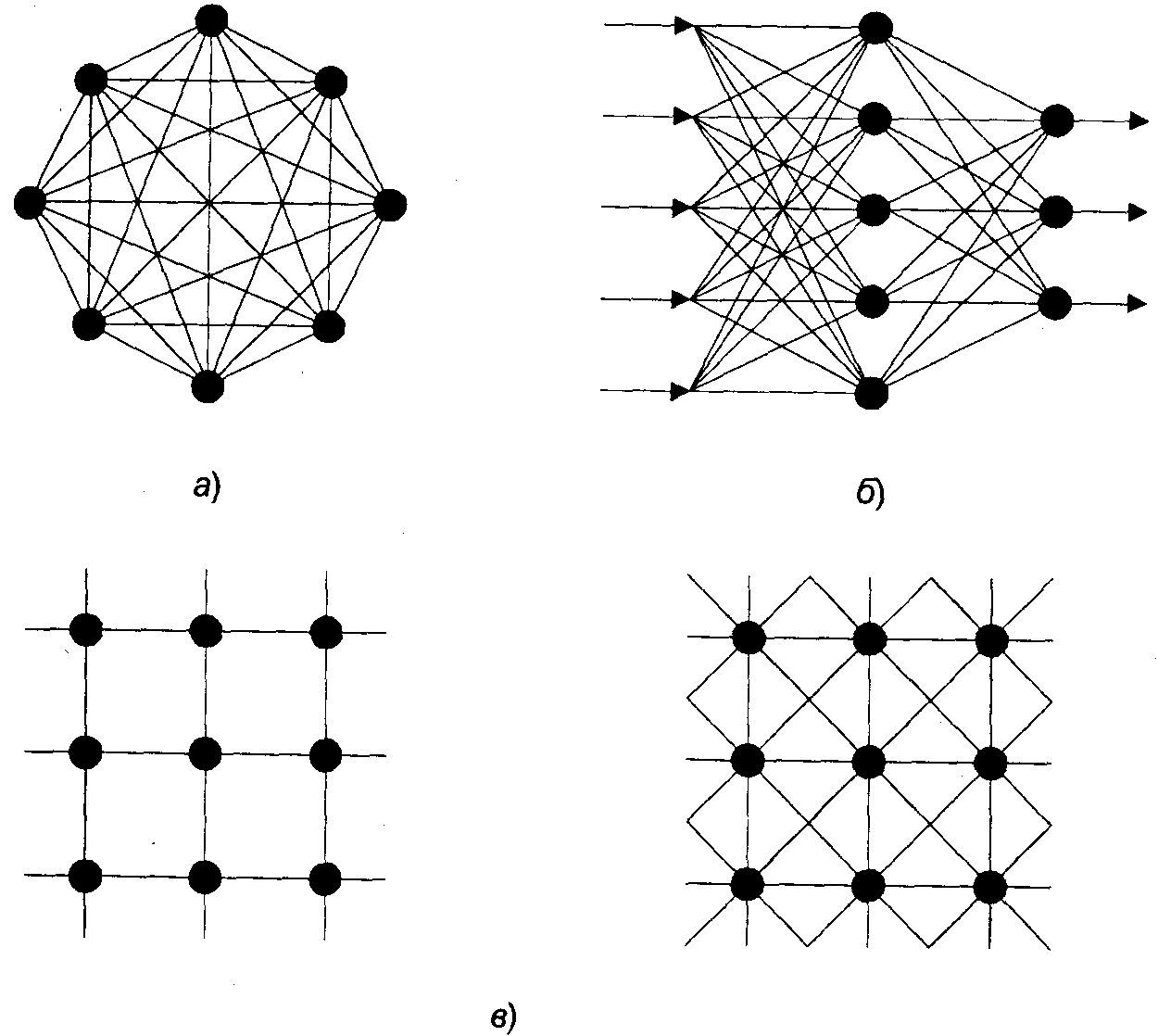
С точки зрения топологии можно выделить три основных ти­па нейронных сетей:

• многослойные или слоистые (рис.2, б);

• слабосвязные (с локальными связями) (рис.2, в).

Рис. 2 Архитектуры нейронных сетей: а-полносвязная сеть, б-многослойная сеть с последовательными связями, в-слабосвязные сети

В полносвязных нейронных сетях каждый нейрон передает свой выходной сигнал остальным нейронам, в том числе и самому себе. Все входные сигналы подаются всем нейронам. Выходными сигналами сети могут быть все или некоторые выходные сигналы нейронов после нескольких тактов функционирования сети.

В многослойных нейронных сетях нейроны объединяются в слои. Слой содержит совокупность нейронов с едиными входными сигналами. Число нейронов в слое может быть любым и не зави­сит от количества нейронов в других слоях. В общем случае сеть состоит из Q слоев, пронумерованных слева направо. Внешние входные сигналы подаются на входы нейронов входного слоя (его часто нумеруют как нулевой), а выходами сети являются выходные сигналы последнего слоя. Кроме входного и выходного слоев в многослойной нейронной сети есть один или несколько скрытых слоев. Связи от выходов нейронов некоторого слоя q к входам нейронов следующего слоя (q +1) называются последовательными.

В свою очередь, среди многослойных нейронных сетей вы­деляют следующие типы.

1) Монотонные. Это частный случай слоистых сетей с дополнительными ус­ловиями на связи и нейроны. Каждый слой кроме вы­ходного разбит на два блока: возбуждающий и тормозящий. Связи между блоками тоже разделяются на тормозящие и возбуждаю­щие. Если от нейронов блока А к нейронам блока В ведут только возбуждающие связи, то это означает, что любой выходной сигнал блока является монотонной неубывающей функцией любого вы­ходного сигнала блока А. Если же эти связи только тормозящие, то любой выходной сигнал блока В является невозрастающей функ­цией любого выходного сигнала блока А. Для нейронов монотон­ных сетей необходима монотонная зависимость выходного сигна­ла нейрона от параметров входных сигналов.

2) Сети без обратных связей. В таких сетях нейроны вход­ного слоя получают входные сигналы, преобразуют их и передают нейронам первого скрытого слоя, и так далее до выходного. Ес­ли не оговорено противное, то каждый выходной сигнал q-гo слоя подастся на вход всех нейронов (q+1)-гo слоя; однако возможен вариант соединения q-го слоя с произвольным (q+р)-м слоем.

Среди многослойных сетей без обратных связей различают полносвязанные (выход каждого нейрона q-ro слоя связан с вхо­дом каждого нейрона (q+1)-го слоя) и частично полносвязанные.

3) Сети с обратными связями. В сетях с обратными связя­ми информация с последующих слоев передается на предыдущие.

Известные нейронные сети можно разделить по типам струк­тур нейронов на гомогенные (однородные) и гетерогенные. Гомо­генные сети состоят из нейронов с единой функцией активации, а в гетерогенную сеть входят нейроны с различными функциями активации.

Существуют бинарные и аналоговые сети. Первые из них оперируют только двоичными сигналами, и выход каждого нейрона может принимать значение либо логического нуля, либо логической единицы.

Сети можно классифицировать по числу слоев. Теоре­тически число слоев и число нейронов в каждом слое может быть произвольным, однако фактически оно ограничено ресурсами ком­пьютера или специализированных микросхем, на которых обычно реализуется нейронная сеть. Чем сложнее сеть, тем более слож­ные задачи она может решать.

Выбор структуры нейронной сети осуществляется в соответ­ствии с особенностями и сложностью задачи. Для решения от­дельных типов задач уже существуют оптимальные конфигурации. Если же задача не может быть сведена ни к одному из известных типов, приходится решать сложную про­блему синтеза новой конфигурации. При этом необходимо руково­дствоваться следующими основными правилами:

• возможности сети возрастают с увеличением числа ней­ронов сети, плотности связей между ними и числом слоев;

• введение обратных связей наряду с увеличением воз­можностей сети поднимает вопрос о динамической устойчивости сети;

• сложность алгоритмов функционирования сети, введение нескольких типов функций активации способствует усилению мощности ней­ронной сети.

Применение нейронных сетей

Вопрос о необходимых и достаточных свойствах сети для решения задач того или иного рода представляет собой целое на­правление нейрокомпьютерной науки. Так как проблема синтеза нейронной сети сильно зависит от решаемой задачи, дать общие подробные рекомендации затруднительно. В большинстве случаев оптимальный вариант получается на основе интуитивного подбо­ра, хотя в литературе приведены доказательства того, что для лю­бого алгоритма существует нейронная сеть, которая может его реализовать.

Многие задачи распознавания образов (зрительных, рече­вых), выполнения функциональных преобразований при обработке сигналов, управления, прогнозирования, идентификации сложных систем, сводятся к следующей математической постановке. Необ­ходимо построить такое отображение X -» У, чтобы на каждый возможный входной сигнал X формировался правильный выход­ной сигнал У. Отображение задается конечным набором пар (, ). Число этих пар (обучающих приме­ров) существенно меньше общего числа возможных сочетаний значений входных и выходных сигналов. Совокупность всех обу­чающих примеров носит название обучающей выборки.

В задачах распознавания образов X — некоторое представ­ление образа (изображение, вектор), У — номер класса, к которому принадлежит входной образ.

В задачах управления X — набор контролируемых парамет­ров управляемого объекта, У — код, определяющий управляющее воздействие, соответствующее текущим значениям контролируе­мых параметров.

В задачах прогнозирования в качестве входных сигналов ис­пользуются временные ряды, представляющие значения контро­лируемых переменных на некотором интервале времени. Выход­ной сигнал — множество переменных, которое является подмноже­ством переменных входного сигнала.

При идентификации X и У представляют входные и выход­ные сигналы системы соответственно.

В результате отображения X -» У необходимо обеспечить формирование правильных выходных сигналов в соответствии:

• со всеми примерами обучающей выборки;

• со всеми возможными входными сигналами, которые не вошли в обучающую выборку.

Второе требование в значительной степени усложняет зада­чу формирования обучающей выборки. В общем виде эта задача в настоящее время еще не решена, однако во всех известных слу­чаях может быть найдено частное решение.

Источник

Классификация нейронных сетей

В настоящее время существует большое разнообразие моделей нейронных сетей. Их различают по структуре сети (связей между нейронами), особенностям модели нейрона, особенностям обучения сети.

По структуре нейронные сети можно разделить на неполносвязные (или слоистые) и полносвязные, со случайными и регулярными связями, с симметричными и несимметричными связями.

По используемым на входах и выходах сигналам нейронные сети можно разделить на аналоговые и бинарные.

По моделированию времени нейронные сети подразделяются на сети с непрерывным и дискретным временем.

По организации обучения разделяют обучение нейронных сетей с учителем (supervised neural networks) и без учителя (non-supervised).

По способу обучения разделяют обучение по входам и по выходам.

По способу предъявления примеров различают предъявление одиночных примеров и «страницы» примеров.

Топология нейронных сетей

Нейронная сеть представляет собой совокупность нейроподобных элементов, определенным образом соединенных друг с другом и с внешней средой с помощью связей, определяемых весовыми коэффициентами В зависимости от функции, выполняемых нейронами в сети, можно выделить три их типа

С точки зрения топологии можно выделить три основных типа нейронных сетей

• полносвязные (рис 3, а),
• многослойные или слоистые (рис 3, б),
• слабосвязные (с локалъными связями) (рис 3, е)

Достоинства и недостатки нейронных сетей как средства для обработки знаний

Если рассматривать нейронную сеть как способ представления знаний, то в ней хранятся знания об ассоциативных связях между стимулами (входными векторами) и откликами (выходными векторами). Знания хранятся (формируются в процессе обучения) обычно в форме весов связей между нейронами.

Недостатками нейронных сетей в качестве метода представления знаний являются:

• трудности вербализации результатов работы нейронной сети и объяснений, почему она приняла то или иное решение;

• невозможность гарантировать повторяемость и однозначность получения результатов.

Преимущества нейронных сетей для представления и обработки знаний:

• отсутствие необходимости формализации знаний, формализация заменяется обучением на примерах;

• естественное представление и обработка нечетких знаний примерно так, как это осуществляется в естественной интеллектуальной системе — мозге;

• ориентация на параллельную обработку, что при соответствующей аппаратной поддержке обеспечивает возможность работы в реальном времени;

• отказоустойчивость и живучесть при аппаратной реализации нейронной сети;

• возможность обработки многомерных (размерности больше трех) данных и знаний без увеличения трудоемкости (но в этом случае затруднено объяснение результатов, так как человек с трудом воспринимает многомерность).

Более детальное толкование ответа на вопрос смотрите в списке в литературы, приведенной ниже.

1. Гаврилова Т. А., Хорошевский В. Ф. Базы знаний интеллектуальных систем. — СПб.: Питер, 2000,

2. Круглов В.В., Дли М.И., Голунов Р.Ю. Нечеткая логика и искусственные нейронные сети – М: Изд-во Физико-математической литературы, 2001.

3. Искусственный интеллект: Справочник. В 3-х кн. Кн. 1. Системы общения и экспертные системы/Под ред. Э.В. Попова. — М.: Радио и связь, 1990.

4. Искусственный интеллект: Справочник. В 3-х кн. Кн. 2. Модели и методы/Под ред. Д.А. Поспелова. — М.: Радио и связь, 1990.

5. Искусственный интеллект: Справочник. В 3-х кн. Кн. 3. Программные и аппаратные средства/Под ред. В.А. Захарова, В.Ф. Хорошевского. — М.: Радио и связь, 1990.

Источник