Временные параметры сетевых графиков
В (табл. 1) приведены основные временные параметры сетевых графиков.
Таблица 1 – Временные параметры сетевых графиков
Элемент сети, характеризуемый параметром
Условное обозначение параметра
Ранний срок свершения события
Поздний срок свершения события
tР (i)
tП (i)
Ранний срок начала работы
Ранний срок окончания работы
Поздний срок начала работы
Поздний срок окончания работы
Полный резерв времени работы
Свободный резерв времени работы
tРН (i, j)
tРО (i, j)
tПН (i, j)
tПО (i, j)
RП (i, j)
RС (i, j)
Продолжительность критического пути
t (L)
Событие не может наступить прежде, чем свершатся все предшествующие работы. Поэтому ранний срок tР (i) свершения i – того события определяется продолжительностью максимального пути, предшествующего этому событию: tР (i)=max t(LПi), где LПi – любой путь, предшествующий i – тому событию, то есть путь от исходного до i –того события сети.
Ранний срок свершения события i – это самый ранний срок, к которому завершаются все работы, предшествующие этому событию.
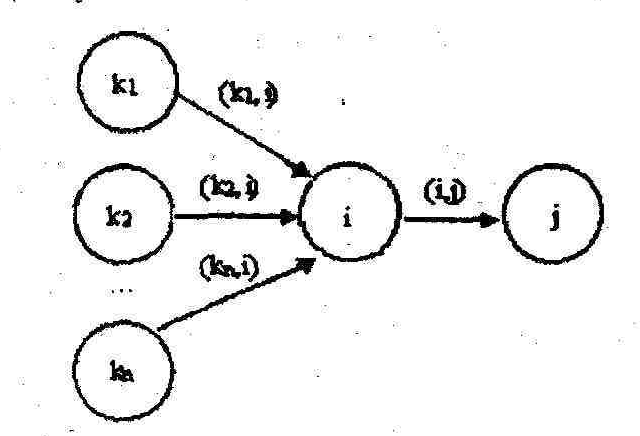
Если событие i имеет несколько предшествующих работ (рис.5), то ранний срок свершения события i находится так:
Пусть B(i) – множество работ, непосредственно предшествующих событию i. Тогда
tР (i)=max< tР (k)+ t (k,i)>,(k,i) B(i) (1)
Задержка свершения события i по отношению к своему раннему сроку не отразится на сроке свершения завершающего события (значит, и на сроке выполнения комплекса работ) до тех пор, пока сумма срока свершения этого события и длины максимального из последующих за ним путей не превысит длины критического пути.
Поэтому поздний срок tП (i) свершения i – того события равен:
tП (i)=tКР – max t(Lci), где Lci – любой путь, следующий за i –м событием, то есть путь от i –того до завершающего события сети.
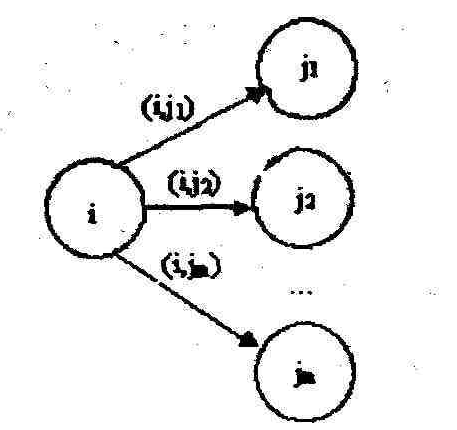
Если событие i имеет несколько последующих работ (рис. 6), то поздний срок свершения события i удобно находить по формуле:
tП (i)= min< tП (j)- t (j,i)>,(j,i) C(i) (2)
где: C(i) – множество работ (j,i), выходящих из вершины i.
При любом поздний срок свершения события i находится так: сначала при i=n полагают tП (i)=tР(n) =tКР, затем последовательно для i равным n-1, n-2,….1 вычисляют по формуле (2).
Резерв времени i – того события определяется как резерв между поздним и ранним сроком его свершения:
Ri = tП(i) – tР(i) (3)
Резерв времени i – того события показывает, на какой допустимый срок можно задержать наступление этого события, не вызывая при этом увеличения времени выполнения комплекса работ.
Критические события резервов времени не имеют, так как любая задержка в свершении события, лежащего на критическом пути, вызовет такую же задержку в свершении завершающего события.
Из этого следует, что для определения критического пути (если он единственный) вовсе не обязательно перебирать все полные пути сетевого графика и определять их длины. Определив ранний срок наступления завершающего события сети, определяют длину критического пути, а выявив события с нулевыми резервами времени, определяют его конфигурацию.
Если критических путей несколько, то выявление их с помощью критических событий может быть затруднительно, так как через часть критических событий могут проходить как критические, так и некритические пути. В этом случае для определения критических путей следует использовать критические работы.
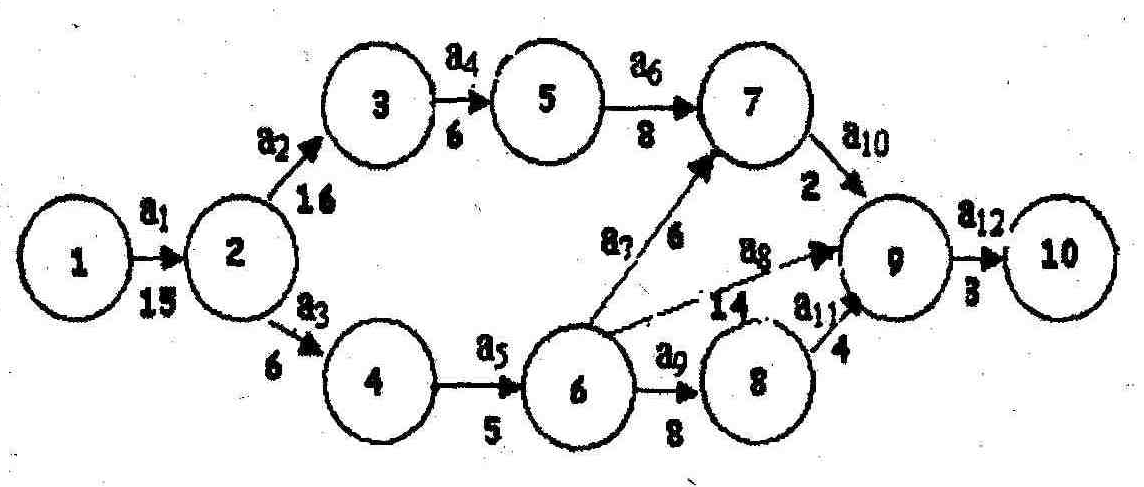
По (рис. 7) рассчитать ранние и поздние сроки свершения событий, а также их резервы. Найти критический путь выполнения комплекса работ и его длину.
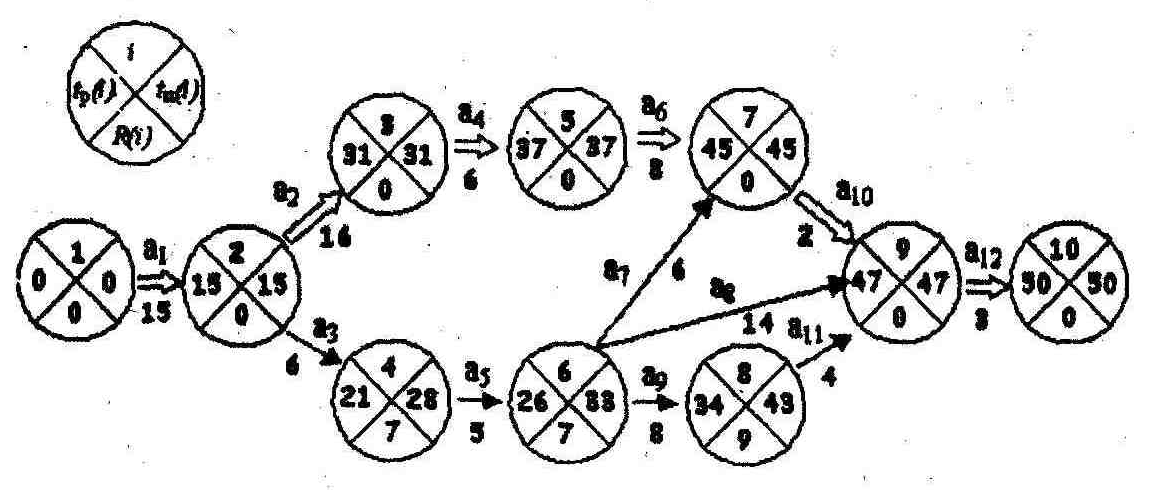
Каждую вершину сети разбиваем на четыре сектора. В верхней части сектора отмечается номер события i, в левой – ранний срок свершения события i, в правой – поздний срок свершения события i, в нижней – резерв времени этого события (рис. 8).
Сначала по формуле (1) находим ранние сроки свершения события i и заносим их в левые секторы сетевого графика. Имеется:
Теперь рассчитываются поздние сроки свершения событий. Расчет начинается с последнего события и затем, «пятясь», двигается к первому событию.
Для i=10 поздний срок свершения события tП (10)= tР (10)=47+3=50. Далее по формуле (2) имеется:
Результаты расчета заносят в правые секторы вершин сети.
По формуле (3) рассчитывают резервы времени каждого события и заносят их в нижние секторы вершин.
R(1) =0-0=0;
R(2) =15-15=0;
Чтобы рассчитать критический путь фиксируются события, не имеющие резервов времени. Это события 1,2,3,5,7,9,10. Следовательно, путь 1→2→3→5→7→9→10 является критическим.
Длина критического пути tКР= tР (10)=50.
Критический путь отмечается на сетевом графике двойной стрелкой.
2.6. Основные параметры сетевой модели
К основным параметрам сетевой модели относятся: критический путь, резервы времени событий и работ. Эти параметры являются исходными для получения ряда дополнительных характеристик, а также для анализа модели.
Критический путь — это наибольший по продолжительности путь сетевой модели от исходного события до завершающего.
В сетевой модели имеются и другие пути, опирающиеся, на исходное и завершающее событие (полные пути), которые могут либо полностью проходить вне критического пути, либо частично совпадать с критической последовательностью работ. Эти пути называются ненапряженными.
Ненапряженные пути — эта полные пути сетевой модели, которые по продолжительности меньше критического пути.
Ненапряженные пути обладают важным свойством: на участках, не совпадающих с критической последовательностью работ они имеют резервы времени. Это означает, что задержка в совершении событий, не лежащих на критическом пути, до определенного момента не влияет на срок завершения разработки в целом. Критические пути резервами времени не располагают.
Поздний срок свершения i-го события — это такой срок свершения i-го события, превышение которого вызовет задержку завершающего события.
Поздний срок свершения i-го события определяется разностью между продолжительностью критического пути и максимального из последующих за данным событием путей до завершающего события:
Тпi = t(Lкр) – t[L(i C) max]
Ранний срок свершения i-го события — минимальный срок, необходимый для выполнения всех работ, предшествующих данному событию.
Ранний срок свершения i-го события определяется как продолжительность во времени максимального из путей, ведущих от исходного события I до данного события i:
Трi = t[L(Ii) max
Резерв времени события — это такой промежуток времени, на который может быть отсрочено свершение события без нарушения сроков завершения разработки в целом.
Резерв времени i-го события определяется как разность между поздним Тпi и ранним Трi, сроками наступления события:
Путь, соединяющий события с нулевыми резервами времени, является критическим.
Резервами времени располагают также работы. Зная ранние и поздние сроки наступления событий, можно для любой работы (i,j) определить ранние и поздние сроки начала и окончания работы.
Ранний срок начала работы (i,j) — минимальное необходимое время между моментом наступления исходного события и моментом начала этой работы.
Ранний срок начала работы (i,j) определяется по формуле:
Поздний срок начала работы (i,j) — максимально допустимый момент начала работы, при котором еще возможно выполнение данной работы и всех следующих за ней работ без превышения критического времени выполнения комплекса работ.
Поздний срок начала работы (i,j) определяется по формуле:
Ранний срок окончания работы (i,j) — минимальное необходимое время между моментом наступления исходного события и моментом окончания этой работы.
Ранний срок окончания работы (i,j) определяется по формуле:
Поздний срок окончания работы (i,j) — максимально допустимый момент окончания данной работы, при котором еще возможно выполнение всех следующих за ней работ без превышения критического времени выполнения комплекса работ.
Поздний срок окончания работы (i,j) определяется по формуле:
Полный резерв времени пути — это разница во времени между длиной критического пути t(Lкр) и длиной любого другого пути t(Ls).
Полный резерв времени пути показывает, насколько могут быть увеличены продолжительности всех работ, принадлежащих пути Ls.
Полный резерв времени пути определяется по формуле:
Полный резерв времени работы Rп ij — максимальное время, на которое можно увеличить продолжительность работы (i,j) или отсрочить ее начало без нарушения позднего срока наступления ее конечного события, не изменяя при этом продолжительности критического пути.
У отдельных работ помимо полного резерва времени имеется свободный резерв времени Rсij, являющийся частью полного резерва.
Свободный резерв времени работы Rс ij — максимальное время, на которое можно увеличить продолжительность работы (i,j) или отсрочить ее начало без нарушения ранних сроков наступления всех последующих событий и работ.
Резервы времени, особенно свободный, позволяют маневрировать сроками начала и окончания работ, их продолжительностью.
Характеристики элементов сетевой модели
При расчетах для сетевой модели определяются следующие характеристики ее элементов.
Характеристики событий
1. Ранний срок свершения события tp(0) = 0, tp(j) = maxitp(i) + t(ij)>, j = 1 – N характеризует самый ранний срок завершения всех путей, в него входящих. Этот показатель определяется «прямым ходом» по графу модели, начиная с начального события сети.
2. Поздний срок свершения события tп(N) = tp(N), tп(i) = minjtп(j) – t(ij)>, i = 1 – (N – 1) характеризует самый поздний срок, после которого остается ровно столько времени, сколько требуется для завершения всех путей, следующих за этим событием. Этот показатель определяется «обратным ходом» по графу модели, начиная с завершающего события сети.
3. Резерв времени события R(i) = tп(i) – tp(i) показывает, на какой максимальный срок можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения всего комплекса работ.
Резервы времени для событий на критическом пути равны нулю, R(i) = 0.
Характеристики работы (I, j)
1. Ранний срок начала работы: t pн ( i , j ) = t p ( i ) .
2. Ранний срок окончания работы: t po ( i , j ) = t pн ( i , j ) + t ij = t p ( i ) + t ij .
3 . Поздний срок начала работы : t пн ( i , j ) = t п ( j ) – t ij .
4 . Поздний срок окончания работ ы : t по ( i , j ) = t п ( j ) .
5. Резервы времени работ:
• полн ы й резерв R п ( i , j ) = t п ( j ) – t p ( i ) – t ij –
макс и м а л ьный за п а с в р емен и , на который можно отсрочить начало или
увеличить длительность работы без увеличения длительности критического пути. Работы на критическом пути не имеют полного резерва времени, для них Rп(i, j) = 0;
• частный резерв R 1 ( i , j ) = R п ( i , j ) – R ( i ) = t п ( j ) – t п ( i ) – t ij –
час т ь полного резерва, н а которую можно увеличить продол ж ительнос т ь
работы, не изменив позднего срока ее начального события;
• свободный резерв R с ( i , j ) = R п ( i , j ) – R ( j ) = t p ( j ) – t p ( i ) – t ij –
макс и м а л ьный запас времен и , на который можно задержа т ь начало работы или
(если она началась в ранний срок) увеличит ее продолжительность, не изменяя ранних сроков начала последующих работ;
• независимый резерв R н ( i , j ) = R п ( i , j ) – R ( i ) – R ( j ) = t p ( j ) – t п ( i ) – t ij –
запас в р емен и , при котором в с е предшеств у ющие работы заканчиваются в
поздние сроки, а все последующие – начинаются в ранние сроки. Использование этого резерва не влияет на величину резервов времени других работ.
Сделаем ряд замечаний. Работы, лежащие на критическом пути, резервов времени не имеют. Если на критическом пути Lкр лежит начальное событие i работы (i, j), то Rп(i, j) = R1(i, j). Если на Lкр лежит конечное событие j работы (i, j), то Rп(i, j) = Rc(i, j). Если на Lкр лежат и событие i, и событие j работы (i, j), а сама работа не принадлежит критическому пути, то Rп(i, j) = Rс(i, j) = Rн(i, j).
Характеристики путей
1. Продолжительность пути равна сумме продолжительностей составляющих ее работ.
2. Резерв времени пути равен разности между длинами критического
пути и рассматриваемого пути.
Резерв времени пути показывает, на сколько может увеличиться продолжительность работ, составляющих данный путь, без изменения
продолжительности срока выполнения всех работ.
В сетевой модели можно выделить так называемый критический путь. Критический путь Lкр состоит из работ (i, j), у которых полный резерв времени равен нулю Rп(i, j) = 0, кроме этого, резерв времени R(i) всех событий i на критическом равен 0. Длина критического пути определяет величину наиболее длинного пути от начального до конечного события сети и равнаtкр = tp(N) = tп(N). Заметим, что в проекте может быть несколько критических путей.
3. Коэффициент напряженности работ
Видно, что Кн(i, j) 1. Чем ближе Кн(i, j) к 1, тем сложнее выполнить данную работу в установленный срок. Напряженность критических работ полагается равной 1. Все работы сетевой модели могут быть разделены на 3 группы: напряженные (Кн(i, j) > 0,8), надкритические (0,6 < Кн(i, j) < 0,8) и резервные (Кн(i, j) < 0,6).
В результате перераспределения ресурсов стараются максимально уменьшить общую продолжительность работ, что возможно при переводе всех работ в первую группу.