Порядок и правила построения сетевых графиков
Сетевые графики составляются на начальном этапе планирования. Вначале планируемый процесс разбивается на отдельные работы, составляется перечень работ и событий, придумываются их логические связи и последовательность выполнения, работы закрепляются за ответственными исполнителями. С их помощью оценивается длительность каждой работы. Затем составляется (сшивается) сетевой график. После упорядочения сетевого графика рассчитываются параметры событий и работ, определяются резервы времени и критический путь. Проводят анализ и оптимизация сетевого графика, который при необходимости вычерчивается заново с пересчетом параметров событий и работ.
При построении сетевого графика необходимо соблюдать ряд правил:
1) все стрелки сетевого графика имеют общее направление (слева направо);
2) между парой событий может быть изображена только одна работа;
3) используются возможные варианты следования событий и работ (табличная запись и пути перехода приведены на рис. 1);
4) в сетевой модели не должно быть «тупиковых» событий, то есть событий, из которых не выходит ни одна работа, за исключением завершающего события;
5) в сетевом графике не должно быть «хвостовых» событий (кроме исходного), которым не предшествует хотя бы одна работа;
6) все события, кроме исходного и завершающего, должны иметь как входящие, так и выходящие стрелки;
7) если две работы начинаются в одно и то же время, в одном событии и оканчиваются в другом событии, то вводят фиктивное событие и фиктивную работу. При этом одна из параллельных работ замыкается на это фиктивное событие. Фиктивные работы имеют нулевую продолжительность и изображаются на графике пунктирными линиями;
8) в сети не должно быть замкнутых контуров и петель, то есть путей, соединяющих некоторые события с ними же самими.
Упорядочение сетевого графика. Понятие о пути
Предположим, что при составлении некоторого проекта выделено 12 событий – 0,1,2,3,4,5,6,7,8,9,10,11 и 24 связывающие их работы – (0,1), (0,2), (0,3), (1,2), (1,4), (1,5), (2,3), (2,5), (2,7), (3,6), (3,7), (3,10), (4,8), (5,8), (5,7), (6,10), (7,6), (7,8), (7,9), (7,10), (8,9), (9,11), (10,9), (10,11). Необходимо составить и упорядочить сетевой график.
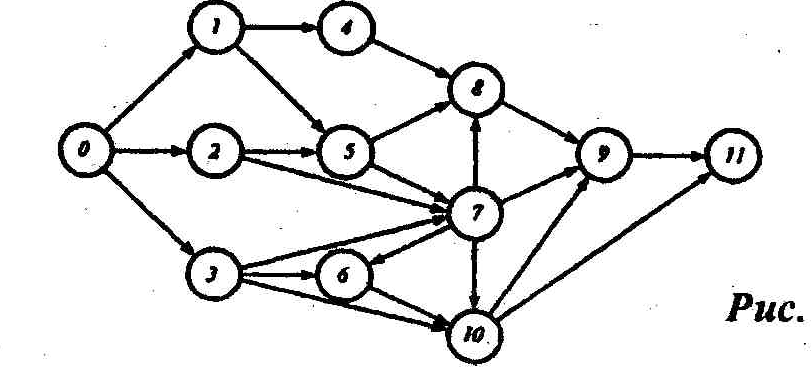
Как следует из перечня работ, исходным событием является событие 0 (ему не предшествуют никакие работы), а завершающим – событие 11 (за ним не следует ни одна работа). Полагая на сетевых графиках изменении времени слева направо, поместим событие 0 в левую часть графика, а событие 11 – в правую часть, разместив между ними промежуточные события в некотором порядке, соответствующем их номерам (рисунок 2). События свяжем работами-стрелками в соответствии с перечнем работ.
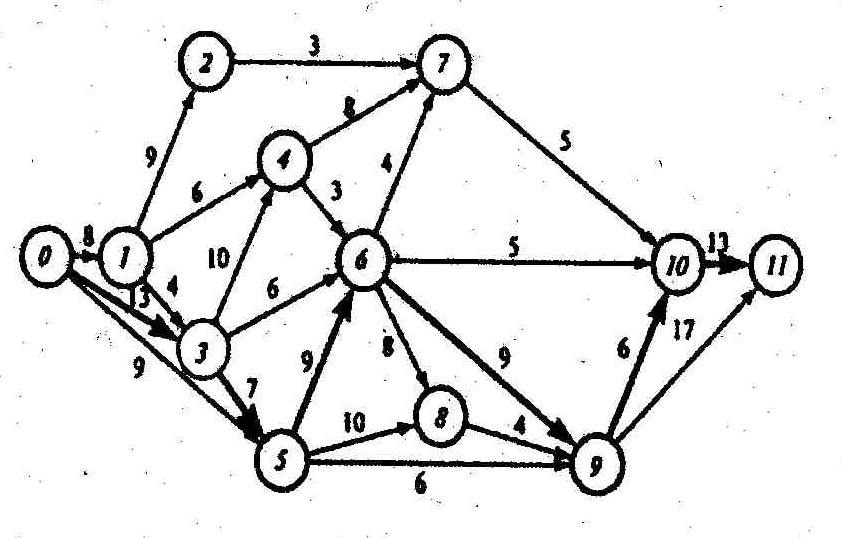
Упорядочение сетевого графика заключается в таком расположении событий и работ, при котором для любой работы предшествующее ей событие расположено левее и имеет меньший номер по сравнению с завершающим эту работу событием. Другими словами, в упорядоченном сетевом графике: от событий с меньшими номерами к событиям с большими номерами (рисунок 3).
Одно из важнейших понятий сетевого графика – понятие пути.
Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы.
Среди различных путей сетевого графика наибольший интерес представляет полный путь L – любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим.
Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими называются также работы и события, расположенные на этом пути.
Например, для рассматриваемого нами сетевого графика (рисунок 3) полными путями будут: путь 0→1→2→7→10→11 продолжительностью 8+9+3+5+13=38 суток, путь 0→1→3→4→6→10→11 продолжительностью 8+4+10+3+5+13=43 суток, путь 0→3→5→6→9→10→11 продолжительностью 13+7+9+13+6+13=61 суток и т.д.
Последний путь имеет наибольшую продолжительность (не только среди приведенных четырех полных путей, но и среди всех полных путей, которых в данном случае насчитывается 64), поэтому он и является критическом. Продолжительность критического пути составляет 61 сутки, то есть для проведения комплекса работ понадобятся 61 сутки. Быстрее комплекс выполнить нельзя, так как для достижения завершающего события критический путь надо пройти обязательно.
Для достижения события 11 надо выполнить работу (10,11), то есть достичь события 10; для достижения события 10 надо провести работу (9,10), то есть достичь события 9; для достижения события 9 надо достичь работу (6,9), то есть достичь события 6, и т.д.
Определив критический путь, установили критические события сети 0,3,5,6,9,10,11 и критические работы (0,3), (3,5), (5,6), (6,9), (9,10), (10,11).
Критический путь имеет особое значение в системе СПУ, так как работы этого пути определяют общий цикл завершения всего комплекса работ, планируемых при помощи сетевого графика. И для сокращения продолжительность проекта необходимо в первую очередь сокращать продолжительность работ, лежащих на критическом пути.
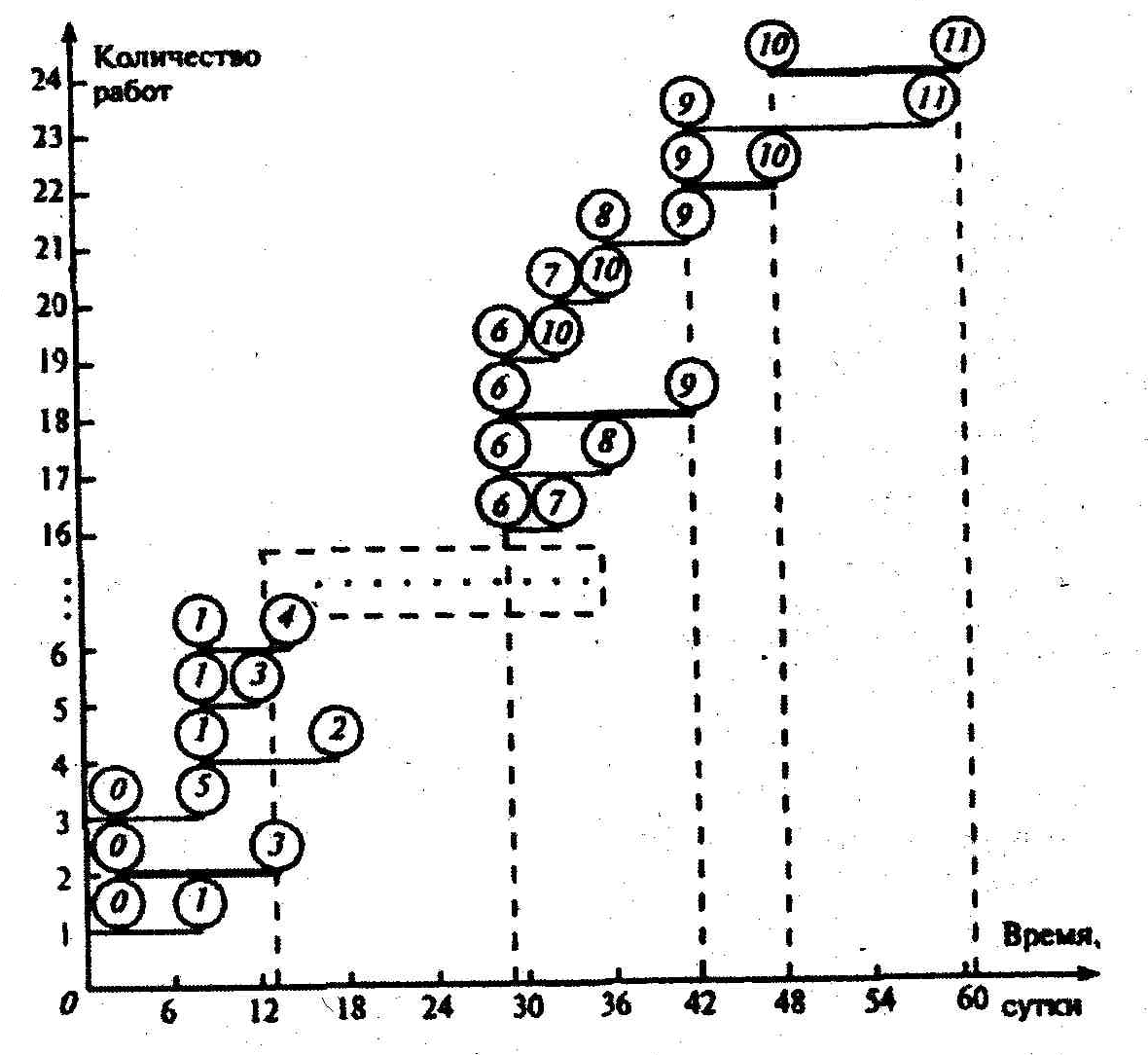
Классический вид сетевого графика – сеть, вычерченная без масштаба времени. Поэтому сетевой график, хотя дает четкое представление о порядке следования работ, но недостаточно нагляден для определения тех работ, которые должны выполняться в каждый данный момент времени. В связи с этим небольшой проект после упорядочения сетевого графика рекомендуется дополнить линейной диаграммой проекта. Такая линейная диаграмма для рассматриваемой сети показана на рисунке 4.
При построении линейной диаграммы каждая работа изображается параллельным оси времени отрезком, длина которого равна продолжительности этой работы. При наличии фиктивной работы нулевой продолжительности (в рассматриваемой сети ее нет) она изображается точкой. События i и j , начало и конец работы (i, j) помещают соответственно в начале и конце отрезка. Отрезки располагают один над другим, снизу вверх в порядке возрастания индекса i , а при одном и том же i – в порядке возрастания индекса j (на рисунке 4 вследствие ограниченности места не показаны работы-отрезки, выходящие из 2-, 3-, 4- и 5-го событий).
По линейной диаграмме проекта можно определить коритическое время, критический путь, а также резервы времени всех работ.
Критическое время комплекса работ равно координате на оси времени самого правого конца всех отрезков диаграммы:
ТКР=t(11) =61 суток
Для определения критического пути рассматриваются работы-отрезки, конечные события которых совпадают с завершающим событием сети (в примере (9,11) и (10,11). Затем находят отрезок (9,10), правый конец которого лежит на одной вертикали (10) с левым концом одного из рассматриваемых ранее отрезков (10,11). Аналогично определяют и другие работы-отрезки критического пути: (6,9),….(0,3) (на рис. 4 они все выделены жирным шрифтом).
Определение критического пути
Будем предполагать, что время выполнения каждой работы точно известно. Введем следующие определения.
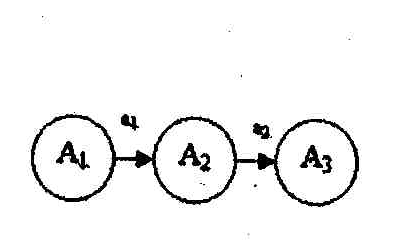
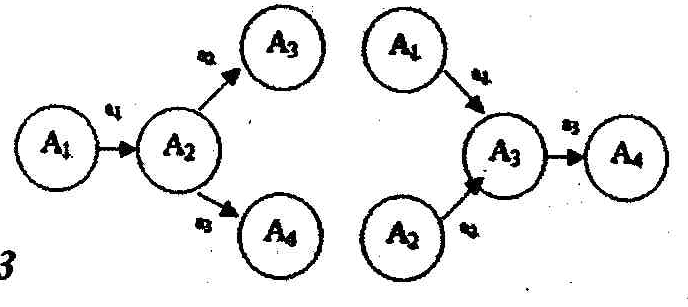
Путь— последовательность взаимосвязанных работ, ведущая из одной вершины проекта в другую вершину. Например (см. Рисунок 48), и – два различных пути.
Рисунок 48. Различные пути на сетевом графике
Длина пути— суммарная продолжительность выполнения всех работ пути.
Полный путь— это путь от исходного к завершающему событию.
Критический путь— полный путь, суммарная продолжительность выполнения всех работ которого является наибольшей.
Очевидно, что минимальное время, необходимое для выполнения любого проекта равно длине критического пути. Именно на работы, принадлежащие критическому пути, следует обращать особое внимание. Если такая работа будет отложена на некоторое время, то время окончания проекта будет отложено на то же время. Если необходимо сократить время выполнения проекта, то в первую очередь нужно сократить время выполнения хотя бы одной работы на критическом пути.
Для того, чтобы найти критический путь, достаточно перебрать все пути и выбрать тот, или те из них, которые имеют наибольшую суммарную продолжительность выполнения работ. Однако для больших проектов реализация такого подхода связана с вычислительными трудностями. Метод критического пути (метод CPM — Critical Path Method) позволяет получить критический путь намного проще.
Расчет сетевой модели начинают с временных параметров событий, которые вписывают непосредственно в вершины сетевого графика (Рисунок 49):
–ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i;
–поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
–резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения.

- для исходного события S:
;
- для всех остальных событий i:
,
где максимум берется по всем работам (k,i), входящим в событие i; 


- для завершающего события F:
;
- для всех остальных событий i:
,
где минимум берется по всем работам (i,j), выходящим из события i; 

- необходимое условие: нулевые резервы событий, лежащих на критическом пути
;
- достаточное условие: нулевые полные резервы работ, лежащих на критическом пути
.
— показывает максимальное время, на которое можно увеличить длительность работы (i,j) или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом.
Пример Рассмотрим пример. Компания разрабатывает строительный проект. Исходные данные по основным операциям проекта представлены в таблице. Нужно построить сетевую модель проекта, определить критические пути и проанализировать, как влияет на ход выполнения проекта задержка работы D на 4 недели.
| Работа | Непосредственно предшествующая работа | Длительность, недели |
| A | — | 4 |
| B | — | 6 |
| C | A, B | 7 |
| D | B | 3 |
| E | C | 4 |
| F | D | 5 |
| G | E,F | 3 |
Сетевой график проекта показан на рисунке ниже (см. Рисунок 52). 
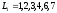


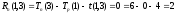



 –ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i;
–ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i; –поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
–поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети; –резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения.
–резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения. ;
; ,
, ;
; ,
, ;
; .
. — показывает максимальное время, на которое можно увеличить длительность работы (i,j) или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом.
— показывает максимальное время, на которое можно увеличить длительность работы (i,j) или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом.