Критический путь и его условия.
Метод критического пути — эффективный инструмент планирования расписания и управления сроками проекта.
В основе метода лежит определение наиболее длительной последовательности задач от начала проекта до его окончания с учетом их взаимосвязи. Задачи лежащие на критическом пути (критические задачи) имеют нулевой резерв времени выполнения и в случае изменения их длительности изменяются сроки всего проекта. В связи с этим при выполнении проекта критические задачи требуют более тщательного контроля, в частности, своевременного выявления проблем и рисков, влияющих на сроки их выполнения и, следовательно, на сроки выполнения проекта в целом. В процессе выполнения проекта критический путь проекта может меняться, так как при изменении длительности задач некоторые из них могут оказаться на критическом пути.
Критерии критического пути:
По величине продолжительности выделяется критический (напряженный) путь, имеющий максимальную продолжительность(tкр), определяющую общий срок выполнения работ графика.
Сроком окончания проекта принимаем продолжительность критического пути, как самой длинной цепочки.
Ненапряженные работы сетевого графика и их характеристика.
По величине продолжительности выделяется критический (напряженный) путь, имеющий максимальную продолжительность(tкр), определяющую общий срок выполнения работ графика
другие пути — некритические (ненапряженные).
Резерв времени l-го пути (Pl) определяется разностью между продолжительностью критического и данного пути.
Некритические пути имеют резервы времен, критический — не имеет.
Ненапряженные пути — это полные пути сетевого графика, которые по своей продолжительности меньше критического пути. Ненапряженные пути имеют на участках, не совпадающих с критическими работами, резервы времени свершения событий. Это значит, что задержка в выполнении тех событий, которые не проходят через критический путь, до определенного этими резервами времени не будет оказывать влияния на расчетные или плановые сроки завершения всего проекта работ. Критические пути такими резервами времени не располагают. Это означает, если расчетное время свершения какого-либо события, находящегося на критическом пути, будет задержано, то этим самым будут отодвинуты на этот же период планируемые сроки наступления завершающего события.
Из ненапряженных путей сетевого графика наибольший интерес должны представлять подкритические пути — ближайшие по продолжительности к критическому, а также остальные, менее напряженные пути.
Элементы сетевого графика.
Графическое изображение сетевой модели, представляет собой сетевой график.
Сетевой график, используется для отражения связей между планируемыми работами, порядка их выполнения, позволяет оперативно анализировать и управлять ходом выполнения всего комплекса работ.
Основными понятиями являются: работа, события, пути.
Работа — это либо любой активный трудовой процесс, требующий затрат времени и ресурсов и приводящий к достижению определенных результатов (событий), либо пассивный процесс («ожидание»), не требующий затрат труда, но занимающий время, либо, наконец, связь между какими-то результатами работ (событиями), называемая фиктивной работой. Обычно действительные работы в сетевом графике обозначаются сплошными стрелками , а фиктивные работы — пунктирными .
Действительная работа (например — подготовка трассы соревнований), требующая затрат труда, материальных ресурсов и времени;
Ожидание — работа не требующая затрат труда и материальных ресурсов, но занимающая некоторое время;
Фиктивная работа (Зависимость) — связь между двумя или более событиями, не требующая затрат труда, материальных ресурсов и времени, но указывающая, что возможность начала одной операции непосредственно зависит от выполнения другой. Продолжительность такой работы = 0.
Всякая работа в сети соединяет два события: предшествующее (являющееся для нее начальным) и следующее за ней (конечное).
Событие — это итог проведенных работ, который дает начало для дальнейших (последующих) работ. Событие не имеет продолжительности во времени. Событие, за которым начинается данная работа, называется начальным для данной работы; оно обозначается символом i. Событие, которое наступает после выполнения данной работы, называется конечным для данной работы; оно обозначается символом j.
В каждой сети имеются два крайних события — исходное и завершающее. Исходным называется событие в сети, не имеющее предшествующих событий и отражающее начало выполнения всего комплекса работ. Оно обозначается символом I. Завершающим называется событие, которое не имеет последующих событий и показывает достижение конечной цели выполнения комплекса работ. Оно обозначается символом К. В одно и то же событие может входить и выходить из него несколько видов работ.
Исходное событие — начало выполнения комплекса работ;
Завершающее событие — конечное событие, означающее достижение конечной цели комплекса работ;
Промежуточное событие, как результат одной или нескольких работ, представляющих возможность начать одну или несколько непосредственно следующих работ. Продолжительность промежуточного события во времени всегда = 0.
Событие определяет состояние, а не процесс.
Путь — это любая последовательность работ в сетевом графике, в котором конечное событие каждой работы совпадает с начальным событием следующей за ней работы. Если известна продолжительность каждой работы tij, то для каждого пути может быть вычислена его общее время выполнения — длина, т. е. общая сумма продолжительности всех работ пути ТLi.
Полный путь — начало которого совпадает с исходным событием сети, а конец — с завершающим, называется полным путем;
Путь, предшествующий событию — путь от исходного события сети до данного события;
Путь, следующий за событием — путь, соединяющий событие с завершающим событием;
Путь между событиями i и j — путь, соединяющий какие-либо два события i и j, из которых ни одно не является исходным или завершающим событием сетевого графика;
Критический путь — путь, имеющий наибольшую продолжительность от исходного события до завершающего.
Определение критического пути
Будем предполагать, что время выполнения каждой работы точно известно. Введем следующие определения.
Путь— последовательность взаимосвязанных работ, ведущая из одной вершины проекта в другую вершину. Например (см. Рисунок 48), и – два различных пути.
Рисунок 48. Различные пути на сетевом графике
Длина пути— суммарная продолжительность выполнения всех работ пути.
Полный путь— это путь от исходного к завершающему событию.
Критический путь— полный путь, суммарная продолжительность выполнения всех работ которого является наибольшей.
Очевидно, что минимальное время, необходимое для выполнения любого проекта равно длине критического пути. Именно на работы, принадлежащие критическому пути, следует обращать особое внимание. Если такая работа будет отложена на некоторое время, то время окончания проекта будет отложено на то же время. Если необходимо сократить время выполнения проекта, то в первую очередь нужно сократить время выполнения хотя бы одной работы на критическом пути.
Для того, чтобы найти критический путь, достаточно перебрать все пути и выбрать тот, или те из них, которые имеют наибольшую суммарную продолжительность выполнения работ. Однако для больших проектов реализация такого подхода связана с вычислительными трудностями. Метод критического пути (метод CPM — Critical Path Method) позволяет получить критический путь намного проще.
Расчет сетевой модели начинают с временных параметров событий, которые вписывают непосредственно в вершины сетевого графика (Рисунок 49):
–ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i;
–поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
–резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения.

- для исходного события S:
;
- для всех остальных событий i:
,
где максимум берется по всем работам (k,i), входящим в событие i; 


- для завершающего события F:
;
- для всех остальных событий i:
,
где минимум берется по всем работам (i,j), выходящим из события i; 

- необходимое условие: нулевые резервы событий, лежащих на критическом пути
;
- достаточное условие: нулевые полные резервы работ, лежащих на критическом пути
.
— показывает максимальное время, на которое можно увеличить длительность работы (i,j) или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом.
Пример Рассмотрим пример. Компания разрабатывает строительный проект. Исходные данные по основным операциям проекта представлены в таблице. Нужно построить сетевую модель проекта, определить критические пути и проанализировать, как влияет на ход выполнения проекта задержка работы D на 4 недели.
| Работа | Непосредственно предшествующая работа | Длительность, недели |
| A | — | 4 |
| B | — | 6 |
| C | A, B | 7 |
| D | B | 3 |
| E | C | 4 |
| F | D | 5 |
| G | E,F | 3 |
Сетевой график проекта показан на рисунке ниже (см. Рисунок 52). 
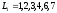


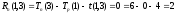



 –ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i;
–ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i; –поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
–поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети; –резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения.
–резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения. ;
; ,
, ;
; ,
, ;
; .
. — показывает максимальное время, на которое можно увеличить длительность работы (i,j) или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом.
— показывает максимальное время, на которое можно увеличить длительность работы (i,j) или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом.