Методы расчета параметров сетевых моделей

Методы расчета сетевых моделей

Расчет сетевой модели заключается в определении его параметров, к которым относятся:

— раннее начало каждой работы — самый ранний срок, когда может быть начата данная работа;

— раннее окончание каждой работы — самый ранний срок, когда может быть завершена данная работа;

— позднее начало каждой работы — самый поздний срок, когда может быть начата данная работа (при условии, что все работы будут завершены к установленному сроку);

— позднее окончание каждой работы — самый поздний срок, когда может быть окончена данная работа (при условии, что все работы будут завершены к установленному сроку);

— полный резерв времени каждой работы — запас времени, которым располагает каждая работа (при условии, что все работы будут завершены к установленному сроку);

— частный резерв времени каждой работы — запас времени, которым располагает каждая работа при условии, что все последующие работы начнутся в ранние сроки. Это резерв времени работ каждой ветви сетевой модели, рассматриваемой в качестве самостоятельной (частной) модели.

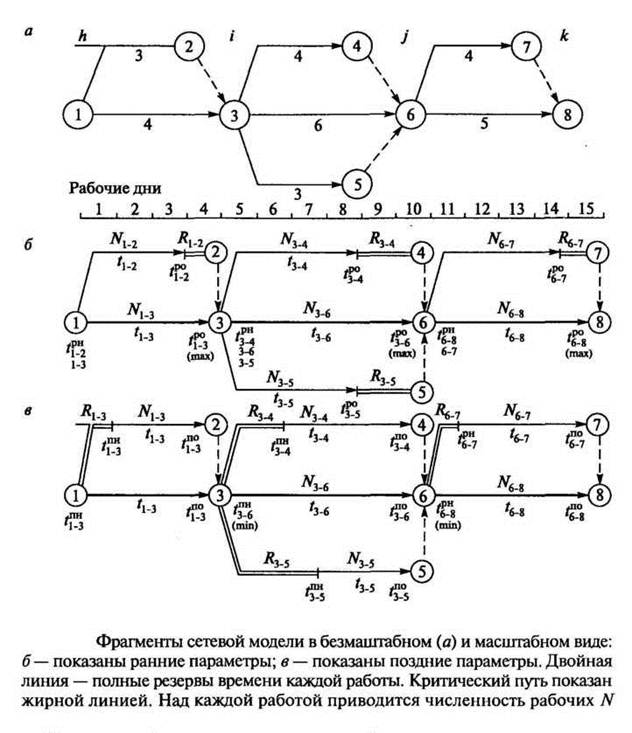
Рассмотрим фрагмент сетевой модели приведенной в масштабный вид, с выполнением работ в ранние (б) и поздние (в) сроки.

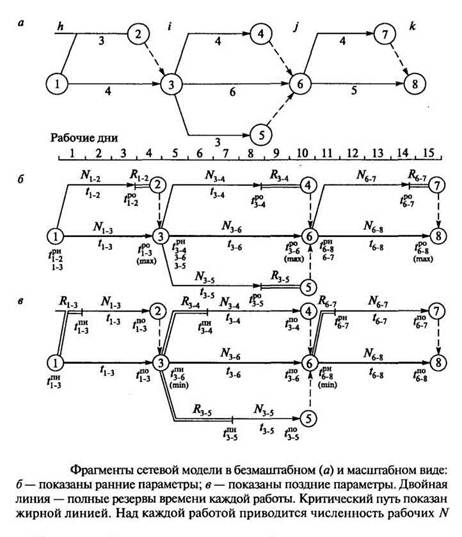Критический путь проходит по тем работам, для которых

Существуют несколько методов расчета: аналитический, табличный, секторный, потенциалов, матричный и другие.

Наиболее распространенными из них являются:

— табличный (модернизированный аналити ческий

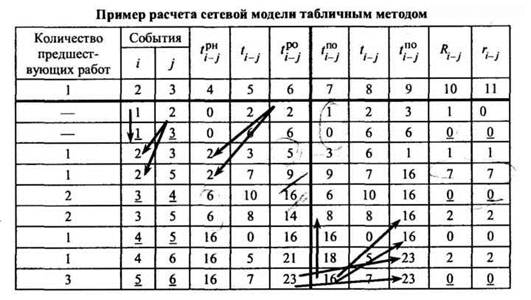
Табличный метод является наиболее универсальным, им могут быть рассчитаны сетевые модели с любым количеством событий, в расчете использована современная вычислительная техника.

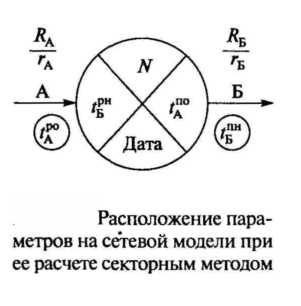
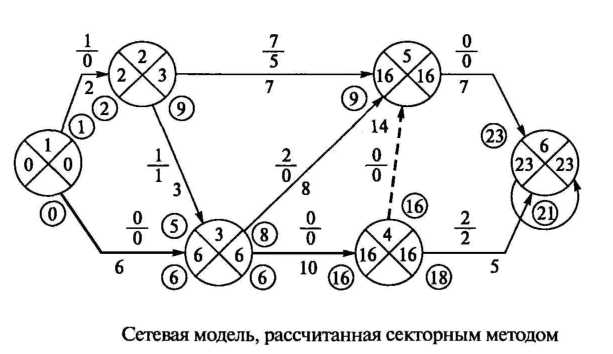
Секторный метод расчета применяют при расчете сетевых моделей с сравнительно небольшим количеством событий. Расчет вы­полняют непосредственно на модели.

Размещение параметров в секторах и на самой модели приведено на рисунке.

Методическая основа расчета та же, что и при табличном методе — используют те же расчетные формулы.

Последовательность расчета — ранние сроки считают слева направо, для последнего события переносят значение t_рн i -j из левого сектора в правый t_по i -j и ведут расчет поздних параметров в обратном порядке — справа налево. Значение резервов записывают над каждой работой.

Источник

24. Методы расчета параметров сетевых моделей. Табличный метод расчета параметров сетевой модели.

Основные параметры сетевых моделей — это критический путь, резервы времени событий, работ и путей.

Методы расчета параметров сетевой модели делятся на две группы.

В первую группу входят аналитические методы, которые включают вычисления по формулам непосредственно на сетевом графике, табличный и матричный методы.

Ко второй группе относятся методы основанные на теории статистического моделирования, которые целесообразно применять при расчете стохастических сетей с очень большим разбросом возможных сроков выполнения работ.

25. Анализ сетевых моделей

Анализ сетевой модели проводим с целью выявления резервов и «узких мест». Однако, большую наглядность все же дает графический метод анализа. Соединение различных методов сетевого моделирования позволяет объединить их преимущества.

Следует помнить, что обнаруженные резервы позволяют более гибко управлять комплексом работ путем их разумного перераспределения с одних работ на другие, не произвольно, а по специальным методам оптимизации.

Анализ сетевой модели начинаем с определения минимального времени выполнения всего комплекса работ. Для этой цели проследим все возможные пути перехода из одного события (0) к завершающему (9). Таких путей четыре:

Определим длительность этих путей:

Т1 = t(L1) = t0,1 + t1,2 + t2,4 + f4,6+ t6,8 + t8,9 = 16 + 16 + 6 + 8 + 2 + 3 = 50 дн.

Т2 = t(L2) = t0,1 + t1,3 + t3,5 + f5,6+ t6,8 + t8,9 =15 + 6 + 5 + 6 + 2 + 3=37дн.

Т3 = t(L3) = t0,1 + t1,3 + t3,5 + f5,6+ t8,9 = 15 + 6 + 5 + 14 + 3 = 43 дн.

Т4 = t(L4) = t0,1 + t1,3 + t3,5 + f5,7+ t7,8 + t8,9 = 15+ 6 + 5 + 8 + 4 + 3 = 41 дн.

Поскольку многие из работ, лежащих на этих путях, выполняются параллельно, общий срок перевода коммерческого предприятия на самообслуживание будет определяться путем максимальной продолжительности, называемым критическим:

Длительность пути L2 составляет t(L2) = 37 дней минимальна, однако не позволяет выполнить все работы комплекса.

Длительность пути L2 составляет t(L2) — 50 дней, однако за это время все работы комплекса могут быть выполнены. Следовательно, минимальное время, за которое может быть выполнен весь комплекс работ, составляет 50 дней, следовательно, путь L1 является критическим.

Теперь определим полные резервы времени по всем путям:

В пределах имеющихся резервов времени с выполнением некоторых работ можно не спешить, и общий срок выполнения комплекса работ не увеличится. Если же длительность выполнения любой из работ критического пути увеличилась, то общий срок выполнения комплекса неизбежно возрастет.

Построение начинается с критического пути LKP в соответствии с правилами сетевого моделирования по графику событий с учетом изображения длительностей работ tij в масштабе времени по оси абсцисс. По оси ординат длины стрелок выбираются из соображений удобства восприятия топологии сети в целом. Этим объясняется большая длина стрелки работы (6,8) в сравнении с работой (4,6), хотя по масштабу времени длительность t4,6 больше t6,8.

Длительность всех остальных путей T2, Т3, Т4 меньше, поэтому вводим фиктивные события 5′, 8′, 7′ и фиктивные работы (5′,6), (8′,8), (7′,8) с нулевой продолжительностью.

В результате мы получили полную картину расположения мест свободных резервов времени работ r5,6C.B =13 дням, r5,8C.B = 7 дням r7,8C.B =9 дням. Наиболее напряженными являются работы критического пути L1, которые не имеют резервов и поэтому являются «узкими местами» комплекса работ.

Таким образом, в результате анализа сетевой модели мы получили все необходимые данные для проведения оптимизации.

Наличие резервов позволит провести оптимизацию сетевого графика путем лучшего перераспределения выделенных ресурсов и построить более экономный план, который даст возможность выполнить весь комплекс работ за меньшее вре

Источник

Параметры сетевых моделей и методы их расчета

Сетевая модель имеет ряд характеристик, которые позволяют определить степень напряженности выполнения отдельных работ, а также всего их комплекса и принять решение о перераспределении ресурсов.
Ранний срок наступления события t_р(i) — самый ранний из возможных сроков наступления события. Он равен продолжительности максимального пути от исходного события до данного.
t_р(i) = max t[L_р(i)] (2.1)
Например, t_р(7)=19, т.к. L₁=(1,2,4,7), L₂=(1,3,4,7),
t(L₁)=5+12=17 < t(L₂)=7+12=19.
Ранний срок начала работы t_р.н.(i,j) равен продолжительности максимального пути от исходного до начального события данной работы.
t_р.н.(i,j)=max t[L_n(i)](2.2)
Например, t_р.н.(7,11)=19, т.к. L₁=(1,2,4,7), L₂=(1,3,4,7),
t(L₁)=5+12=17 2)=7+12=19.
Ранний срок начала работы равен раннему сроку наступления начального события данной работы.
t_р.н.(i,j) = t_р(i) (2.3)
Ранний срок окончания работы t_р.о.( i,j) равен сумме раннего срока начала работы и продолжительности данной работы.
t_р.о.(i,j)= t_р.н.(i,j) + t(i,j) (2.4)
Например, t_р.о.(7,11)= t_р.н.(7,11) + t(7,11)= 19+8=27.
Поздний срок наступления события t_п( i) равен разности между продолжительностью критического пути и продолжительностью максимального пути от данного события до завершающего.
t_п(i) =T_кр — max t[L_к(i)](2.5)
Например, t_п(7)=19, т.к. L₁=(7,11), L₂=(7,9,11), t(L₁)=8 > t(L₂)=4,
t_п(7) = T_кр — max t[L_к(7)]=27 — 8=19.
Для событий критического пути t_р( i)=t_п(i), для других событий t_р(i)t_п(i).
Поздний срок окончания работы t_п.о.( i,j) – это самый поздний срок окончания работы, при котором планируемый срок окончания проекта не меняется, он равен разности между продолжительностью критического пути и продолжительностью максимального пути от конечного события данной работы до завершающего события.
t_п.о.(i,j)=T_кр — max t[L_к(j)] (2.6)
Поздний срок окончания работы равен позднему сроку наступления конечного события t_п.о.(i,j) = t_п(j). Например, t_п.о.(4,7) = t_п(7)=19.
Поздний срок начала работы t_п.н.( i,j) – самый поздний срок начала работы, при котором планируемый срок окончания проекта не меняется.
t_п.н.(i,j)= t_{п .о.}(i,j) — t(i,j) (2.7)
Например, t_п.н.(4,7)= t_п.о.(4,7) — t(4,7)=19-12=7.
Для работ критического пути ранние и поздние сроки начала и окончания работ равны: t_р.н.(4,7)= t_п.н.(4,7)=7, t_р.о.(4,7)= t_п.о.(4,7)=19.
Работы, не лежащие на критическом пути, могут иметь резервы времени.
Полный резерв времени R_п( i,j) – максимальное время, на которое можно увеличить продолжительность данной работы, не изменяя продолжительности критического пути.
R_п (i,j)= t_п(j) — t_р(i) — t(i,j)
R_п(i,j)= t_п.н (i,j) — t_р.н.(i,j) (2.8)
R_п (i,j)= t_п.о.(i,j) — t_р.о.(i,j)
Свободный резерв времени R_с( i,j) равен разности между ранним началом последующей работы и ранним окончанием рассматриваемой работы.
R_с(i,j)= t_р.н (j,к) — t_р.о.(i,j) (2.9) Перейти к онлайн решению своей задачи

Читайте также:  Максимальный полный путь сетевой модели это критический путь

Источник

4.Методы расчета параметров сетевой модели.

Для расчета параметров сетевой модели применяют следующие три метода:

• метод вычислений непосредственно на сетевой модели;
• матричный метод;
• табличный метод.

Матричный и табличный методы применяются, как правило, при расчете параметров с помощью ЭВМ,

Рассмотрим более подробно метод расчета параметров непосредственно на сетевой модели. При данном методе расчета, каждый круг, соответствующий каждой вершине графа (событию) разбивается на четыре сектора, где записывают:

Расчет параметров ведется в следующей последовательности:

• определяют tpi –(ранний срок наступления события) – как сумму раннего срока наступления предшествующего ему события и продолжительности работы их соединяющей, т. е. tpi = tpi-1 = ti-1, i. Если к событию подходит две или более работы, то указанная сумма рассчитывается для каждой из работ, максимальная из сумм является ранним сроком наступления события и записывается в левом секторе. Расчет ведется последовательно от исходного события к завершающему;
• определяют tni (поздний срок наступления события) – как разность между поздним сроком наступления непосредственно следующего за ним события и продолжительностью работы их соединяющим, т. е.

Если из события выходит две или более работ, то указанная разность рассчитывается для каждой из работ, минимальная из разностей является поздним сроком наступления данного события записывается в правом секторе. Расчет ведется последовательно от завершающего события к исходному. Для завершающего события ранний и поздний сроки его наступления равны между собой и равны критическому времени;

• определяют резерв времени события ( ), как разность между поздним и ранним сроками его наступления. Записывают в нижнем секторе.

Остальные параметры сетевой модели рассчитывают по ранее рассмотренным зависимостям. Данные расчеты заносят в таблицу.

Источник