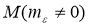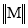Методы шифрования данных в компьютерных сетях

Шифрование в каналах связи компьютерной сети

Одной из отличительных характеристик любой компьютерной сети является ее деление на так называемые уровни, каждый из которых отвечает за соблюдение определенных условий и выполнение функций, необходимых для общения между компьютерами, связанными в сеть. Это деление на уровни имеет фундаментальное значение для создания стандартных компьютерных сетей. Поэтому в 1984 г. несколько международных организаций и комитетов объединили свои усилия и выработали примерную модель компьютерной сети, известную под названием OSI (Open Systems Interconnection — Модель открытых сетевых соединений).

Согласно модели OSI коммуникационные функции разнесены по уровням. Функции каждого уровня независимы от функций ниже- и вышележащих уровней. Каждый уровень может непосредственно общаться только с двумя соседними. Модель OSI определяет 7 уровней: верхние 3 служат для связи с конечным пользователем, а нижние 4 ориентированы на выполнение коммуникационных функций в реальном масштабе времени.

Теоретически шифрование данных для передачи по каналам связи компьютерной сети может осуществляться на любом уровне модели OSI. На практике это обычно делается либо на самых нижних, либо на самых верхних уровнях. Если данные шифруются на нижних уровнях, шифрование называется канальным, а если на верхних, то такое шифрование называется сквозным. Оба этих подхода к шифрованию данных имеют свои преимущества и недостатки.

Канальное шифрование

При канальном шифровании шифруются абсолютно все данные, проходящие по каждому каналу связи, включая открытый текст сообщения, а также информацию о его маршрутизации и об используемом коммуникационном протоколе. Однако в этом случае любой интеллектуальный сетевой узел (например, коммутатор) будет вынужден расшифровывать входящий поток данных, чтобы соответствующим образом его обработать, снова зашифровать и передать на другой узел сети.

Тем не менее канальное шифрование представляет собой очень эффективное средство защиты информации в компьютерных сетях. Поскольку шифрованию подлежат все данные, передаваемые от одного узла сети к другому, у криптоаналитика нет никакой дополнительной информации о том, кто служит источником этих данных, кому они предназначены, какова их структура и т. д. А если еще позаботиться и о том, чтобы, пока канал простаивает, передавать по нему случайную битовую последовательность, сторонний наблюдатель не сможет даже сказать, где начинается и где заканчивается текст передаваемого сообщения.

Не слишком сложной является и работа с ключами. Одинаковыми ключами следует снабдить только два соседних узла сети связи, которые затем могут менять используемые ключи независимо от других пар узлов.

Самый большой недостаток канального шифрования заключается в том, что данные приходится шифровать при передаче по каждому физическому каналу компьютерной сети. Отправка информации в незашифрованном виде по какому-то из каналов ставит под угрозу обеспечение безопасности всей сети. В результате стоимость реализации канального шифрования в больших сетях может оказаться чрезмерно высокой.

Кроме того, при использовании канального шифрования дополнительно потребуется защищать каждый узел компьютерной сети, по которому передаются данные. Если абоненты сети полностью доверяют друг другу и каждый ее узел размещен там, где он защищен от злоумышленников, на этот недостаток канального шифрования можно не обращать внимания. Однако на практике такое положение встречается чрезвычайно редко. Ведь в каждой фирме есть конфиденциальные данные, знакомиться с которыми могут только сотрудники одного определенного отдела, а за его пределами доступ к этим данным необходимо ограничивать до минимума.

Источник

Информационная безопасность и способы шифрования информации в компьютерных сетях

Сагатова, C. М. Информационная безопасность и способы шифрования информации в компьютерных сетях / C. М. Сагатова. — Текст : непосредственный // Молодой ученый. — 2018. — № 28 (214). — С. 5-7. — URL: https://moluch.ru/archive/214/52054/ (дата обращения: 14.07.2023).

Уменьшение затрат времени на криптографические преобразования при реализации блочных шифров является оптимальной задачей защиты информации, поскольку использование таких преобразований не должно снижать производительность компьютерных систем и сетей. Для решения данной задачи предложены множество специальных способов шифрования [1], основанные на применении перестановок, подстановок, логических преобразований и арифметических операций. Комбинирование перестановок, подстановок и логических преобразований позволяет значительно расширить класс возможных недорогих микроэлектронных шифрирующих устройств, обеспечивающих скорость шифрации до 1 Гб бит/сек. Эти способы шифрования ориентированы на использование в составе комбинированных криптографических систем с целью повышения криптостойкости их при минимальных временных затратах.

В данной статье предлагается специальный способ шифрования и структура специализированного вычислительного устройства для его реализации.

Данный способ шифрования основывается на математических операциях над матрицами, т. е. на операциях умножения вектора на матрицу (DМ=В при шифрации и BМ -1 =D при дешифровании) [2].

Рассмотрим алгоритм шифрования данных согласно выражениюDМ=В.

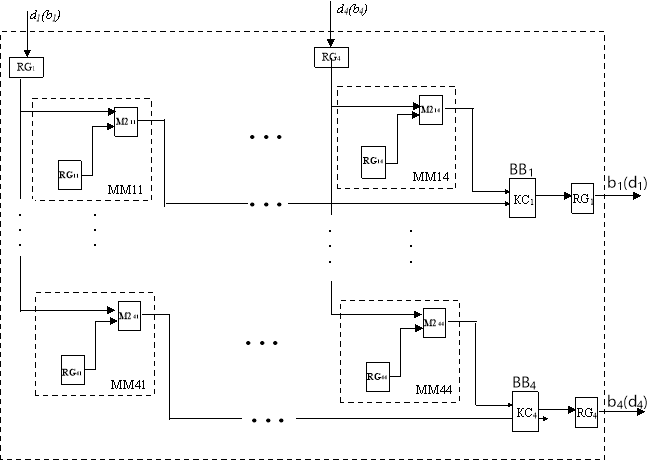
Пусть, заданы четырехмерный вектор D, и четырехмерная квадратная матрица М_ij. Требуется определить четырехмерный вектор В.

ВыраженияDМ=В можно представить в следующем виде:

=,

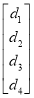
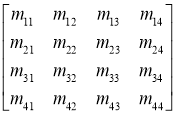
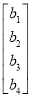
Для реализации обратного процесса, т. е. для дешифрования или восстановления D необходимо определить обратную матрицу М -1 . Определение исходного вектора D реализуется согласно с выражением:

=.

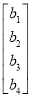
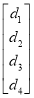
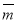
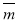
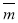
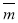
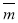
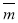
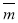
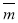
d₁=b_{1 11}+b_{2 12}+b_{3 13}+b_{4 14}; d₂=b_{1 21}+b_{2 22}+b_{3 23}+b_{4 24};

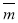
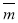
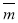
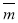
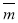
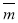
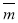
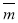
d₃=b_{1 31}+b_{2 32}+b_{3 33}+b_{4 34}; d₄=b_{1 41}+b_{2 42}+b_{3 43}+b_{4 44};.

Единственным условием выполнения обратности процесса является неравенство нулю элементов матриц .

Для шифрования исходный текст разбивается на векторы (В) длиной один байт и каждый вектор перемножается на квадратную матрицу (). Каждый вектор шифрируется независимо от других, поэтому можно осуществить передачу блоков данных и произвольный доступ к запрограммированным данным.

Достоинством данного способа является его гибкость при реализации и использовании в различных приложениях обработки информации.

Предложенный способ может быть реализован аппаратно и программно, но предпочтение отдается аппаратной, т. к. высокая оперативность выполнения шифрования обеспечивается при аппаратной реализации [3].

Рассмотрим вкратце структурную схему устройства шифрования данных с использованием операций над матрицами (Рис.1).

Рис. 1. Структурная схема устройства криптации с использованием операций над матрицами.

Устройство выполняет операцию перемножения матрицы М (обратной матрицы М -1 ) на вектор D(В) и состоит из четырех 8-разрядных RG₁. RG₄, четырех векторов-вычислителей ВВ₁. ВВ₄. Каждый вектор-вычислитель состоит из четырехвходового комбинационного сумматора KCi, второго 8-разрядного регистра и множительных модулей MM_i1. MM_i4. Каждый множительный модуль MMij(j=1. 4) состоит из третьего 8-разрядного регистра RG_ij и множителя Mij.

Как шифрование, так и дешифрование данных в устройстве осуществляется в 4 этапа.

Для дешифрования данных в буферные регистры RG_j вводятся значение вектора В, а в регистры RG_ij соответствующие элементы обратной матрицы М -1 .

Первый этап. Значение вектора D (В) вводится через буферные регистры RG_j, а значения матрицы М через регистры памяти RG_ij.

Второй этап. Выполняются операции умножения значения векторов с элементами матрицы в множительных модулях ММ_ij.

Третий этап. Полученные результаты (т. е. произведения) в модулях умножения ММ_ij суммируются в соответствующих комбинационных сумматорах KC_j.

Четвертый этап. Вычисленные значения (т. е. значение вектора В (D)) на выходах сумматоров KC_j передаются на сдвигающий регистр RG.

Предложенные в работе специальный способ и аппаратное средство шифрования информации в компьютерных сетях, позволяют организовать системы защиты информации, отличающиеся высоким быстродействием и простой реализацией.

1. В. Ф. Шаньгин. Информационная безопасность компьютерных систем и сетей: Учебное пособие — М.: ИД ФОРУМ: НИЦ ИНФРА — М, 2014 г. — С.416.
2. Каримов М. М. Применение аппаратных средств защиты информации в компьютерных сетях / Сбор.научн.трудов ИПМЭ НАН Украины.Киев,2001,вып.9.- С. 8–14
3. Платонов В. В. Программно-аппаратные средства защиты информации: учебник для студ. учреждений высш. проф. Образования /
4. В. В.Платонов.  М.: Издательский центр «Академия», 2013 г. С.336.

Основные термины (генерируются автоматически): обратная матрица, дешифрование данных, значение вектора В, использование операций, специальный способ шифрования, способ шифрования, четырехмерный вектор, этап.

Похожие статьи

Реализация Windows-приложения, выполняющего шифрование.

Ключевые слова:шифрование, дешифрование, шифр Цезаря, шифр Хилла, криптология.

Криптография — это наука о защите данных путем шифрования, а криптоанализ — наука получения сведений о секретной

Затем матрица C умножается на вектор v1 по модулю 33.

Алгоритмы шифрования данных | Статья в журнале.

Панасенко, С. П. Алгоритмы шифрования. Специальный справочник. /

Такой способ шифрования называют шифрование—дешифрирование—шифрование. Если блочный алгоритм использует n-битовый ключ, то длинна ключа в таком методе шифрования будет 2n.

Анализ применения гомоморфных схем шифрования.

Дешифрование, : Расшифровка шифрованного текста c производится путем оценки

Производительность (скорость работы) алгоритма шифрования зависит от вычислительной сложности выполняемых операций, а также от конкретного способа реализации алгоритма.

Особенности оценки качества и оптимизации алгоритмов.

Данный способ предусматривает предварительное вычисление (на этапе программной реализации алгоритма) значений некоторых

Использование данного набора инструкций значительно сокращает время шифрования и дешифрования по данному алгоритму.

Создание криптографии с помощью модулярной математики

Ключевые слова:шифрование, дешифрование, шифр Цезаря, шифр Хилла, криптология. Криптография — это наука о защите данных путем шифрования, а

Для уменьшения количества модульных операции для выполнения арифметических операций с точками.

Особенности проектирования и криптоанализа асимметричной.

В системе RSA шифрование выполняется путем возведения в степень кодов символов

Таблица 1 дает представление о значениях величины . Число операций для каждого

Рассмотрим три способа, которыми может воспользоваться криптоаналитик для раскрытия.

Методология сравнения потоковых шифров | Статья в журнале.

DES, ключ, алгоритм, способ шифрования, тройное шифрование, блочный алгоритм, метод шифрования

Алгоритмы шифрования данных | Статья в журнале.

Реализация Windows-приложения, выполняющего шифрование и дешифрование текста шифрами Цезаря и Хилла.

Некоторые аспекты криптографического взлома и повышения.

Такой способ шифрования называют шифрование—дешифрирование—шифрование.

Алгоритмы шифрования данных | Статья в журнале.

Ключевые слова:шифрование, дешифрование, шифр Цезаря, шифр Хилла, криптология.

Сокрытие информации в коэффициентах спектральных.

Существует два подхода к решению данной проблемы: шифрование информации и

Методы сокрытия, основанные на использовании специальных свойств компьютерных форматов

Получатель знает бинарную матрицу , составляет вектор и производит операцию умножения в .

Источник