2.3. Диаграмма Ганта и сетевой график
Диаграммы Ганта – один из популярных методов планирования проектов. Диаграммы визуализируют план проекта и наглядно показывают, что именно должно быть сделано, сколько времени займет выполнение каждой задачи, в каком порядке они будут выполняться, кто ответственен за их выполнение и сколько все это будет стоить.
Типичная диаграмма Ганта представляет собой график, на котором по горизонтали отложена шкала времени, а по вертикали расположен список задач. Задачи отображаются на графике в виде прямоугольных горизонтальных отрезков. Длина отрезка пропорциональна длительности задачи. Начало и конец отрезка соответствуют началу и концу задачи. Рядом с отрезком отображается дополнительная информация о задаче — стоимость, исполнитель, используемые ресурсы. Площадь отрезка частично заштриховывается — в соответствии с процентом выполнения задачи. Диаграммы позволяют визуально оценить последовательность и длительность задач, входящих в проект, сравнить планируемый и реальный ход выполнения проекта. Определить, сколько ресурсов имеется и сколько потребуется, какие работы необходимо будет выполнить, оценить длительность и стоимость каждой части проекта.
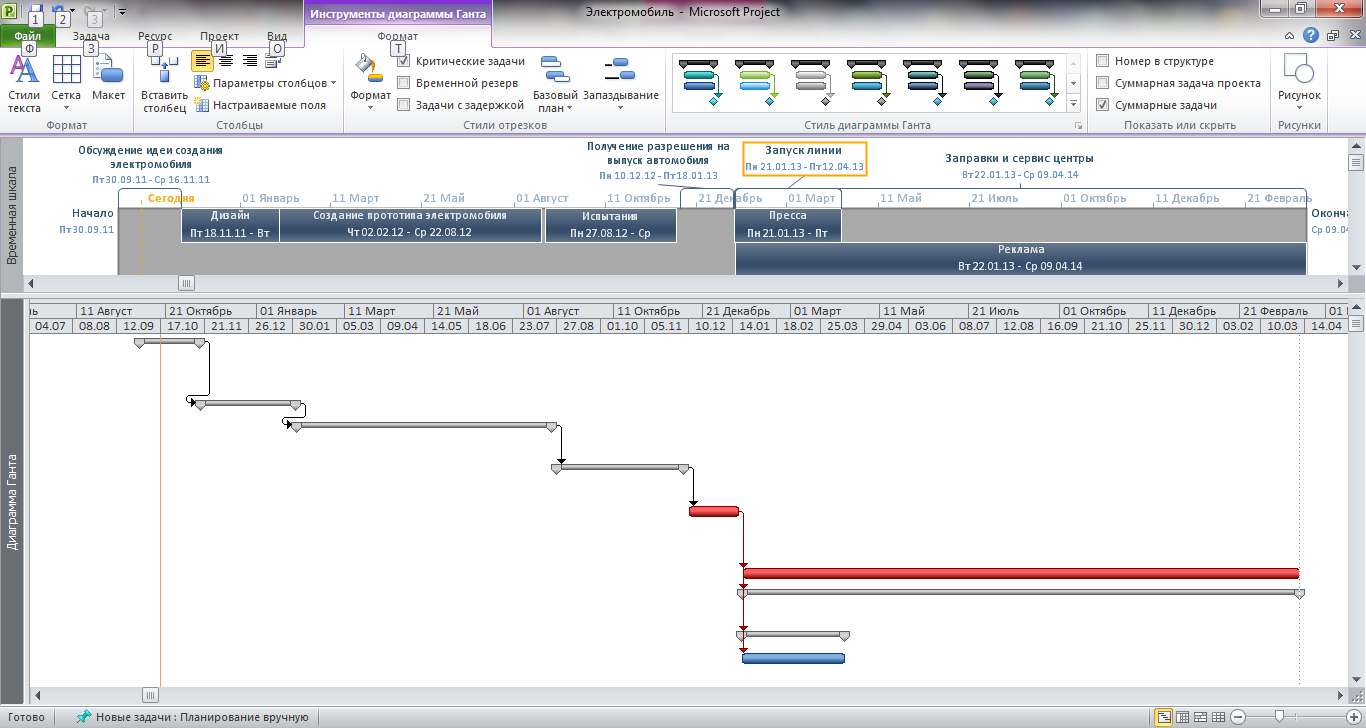
Для удобства представления на рисунке 2.1. представлена общая диаграмма Ганта.
На графиках красным цветом представлен критический путь. Серым цветом показаны этапы, которые имеют работы. Детализированное представление этих этапов представлено на рисунке 2.2.-2.6.
Сетевой график — это динамическая модель производственного процесса, отражающая технологическую зависимость и последовательность выполнения комплекса работ, увязывающая их свершение во времени с учетом затрат ресурсов и стоимости работ с выделением при этом узких (критических) мест. Основные элементы сетевого графика — работа и событие. Работа отражает трудовой процесс, в котором участвуют люди, машины, механизмы, материальные ресурсы, либо процесс ожидания (твердение бетона, сушка штукатурки и т. п.). Каждая работа сетевого графика имеет конкретное содержание. Работа как трудовой процесс требует затрат времени и ресурсов, а как ожидание — только времени. Для правильного и наглядного отображения порядка предшествования работ при построении сети используют изображаемые штриховыми линиями дополнительные дуги, называемые фиктивными работами или связями. Они не требуют ни времени, ни ресурсов, а лишь указывают, что начало одной работы зависит от окончания другой.
Событие выражает факт окончания одной или нескольких непосредственно предшествующих (входящих в событие) работ, необходимых для начала непосредственно следующих (выходящих из события) работ. Событие, стоящее в начале работы, называется начальным, а в конце — конечным. Начальное событие сетевого графика называется исходным, а конечное — завершающим. Событие, не являющееся ни исходным, ни завершающим, называется промежуточным. В исходное событие сетевого графика не входит, а из завершающего не выходит ни одна работа. В отличие от работ, события совершаются мгновенно без потребления ресурсов.
Обозначение непосредственно предшествующих и непосредственно следующих работ. Любая последовательность работ в сетевом графике, при котором конечное событие каждой работы совпадает с начальным событием последующей, называется путем. Продолжительность пути определяется суммой продолжительностей составляющих его работ. Путь наибольшей длины между исходными и завершающими событиями называется критическим (Lm).
Если критическое время не соответствует заданному или нормативному, сокращение сроков производственного процесса необходимо начинать с сокращения продолжительности критических работ.
Сетевой график для данного проекта представлен на рисунке 2.7.
Рисунок 2.1. – Общая диаграмма Ганта.
Рисунок 2.2. – Диаграмма Ганта «Обсуждение идеи создания автомобиля»
Рисунок 2.3. – Диаграмма Ганта «Дизайн»
Рисунок 2.4. – Диаграмма Ганта «Создание прототипа электромобиля»
Рисунок 2.5. – Диаграмма Ганта «Испытание электромобиля»
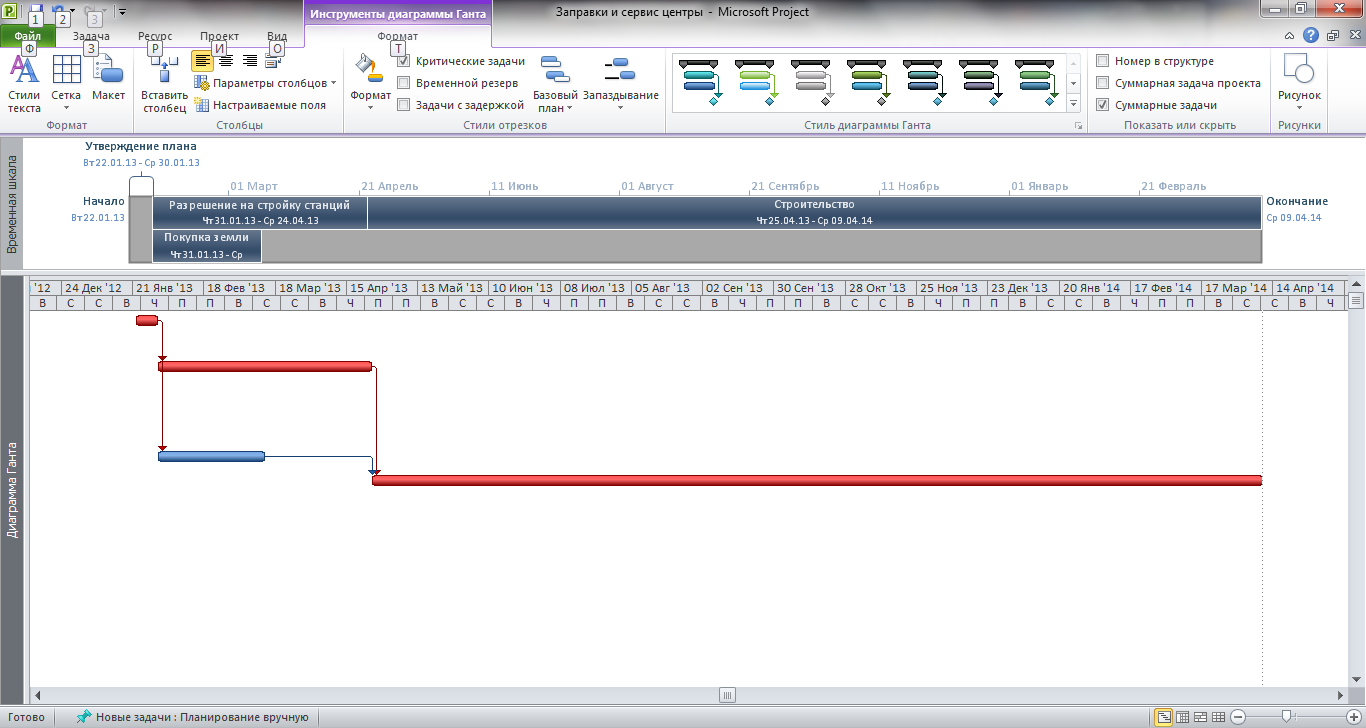
Рисунок 2.6. – Диаграмма Ганта «Строительство станций заправок»
Рисунок 2.7. – Сетевой график
Правила построения сетевых графиков
Для построения сетевого графика необходимо выявить последовательность и взаимосвязь работ: какие работы необходимо выполнить, и какие условия обеспечить, чтобы можно было начать данную работу, какие работы можно и целесообразно выполнять параллельно с данной работой, какие работы можно начать после окончания данной работы. Эти вопросы позволяют выявить технологическую взаимосвязь между отдельными работами, обеспечивают логическое построение сетевого графика и его соответствие моделируемому комплексу работ.
Уровень детализации сетевого графика зависит от сложности строящегося объекта, количества используемых ресурсов, объёмов работ и продолжительности строительства.
Имеется два типа сетевых графиков:
Сетевые графики типа «вершины — работы».
Элементами такого графика являются работы и зависимости. Работа представляет собой определенный производственный процесс, требующий затрат времени и ресурсов для его выполнения, и изображается прямоугольником. Зависимость (фиктивная работа) показывает организационно-технологическую связь между работами, не требующую затрат времени и ресурсов, изображается стрелкой. Если между работами имеется организационный или технологический перерыв, то на зависимости указывается длительность этого перерыва. Пример сетевого графика «вершины — работы» приведен на рис. 6.1.
Рис. 6.1. Сетевой график типа «вершины — работы»
Если работа сетевого графика «вершины — работы» не имеет предшествующих работ, то она является исходной работой этого графика. Если работа не имеет последующих работ, то она является завершающей работой сетевого графика. В сетевом графике «вершины — работы» не должно быть замкнутых контуров (циклов), т.е. зависимости не должны возвращаться в ту работу, из которой они вышли.
Сетевые графики типа «вершины-события».
Элементами такого типа графиков являются работы, зависимости и события. Работа изображается сплошной стрелкой, зависимость – пунктирной. Событие представляет собой результат одной или нескольких работ, необходимый и достаточный для начала одной или нескольких последующих работ, и изображается кружком.
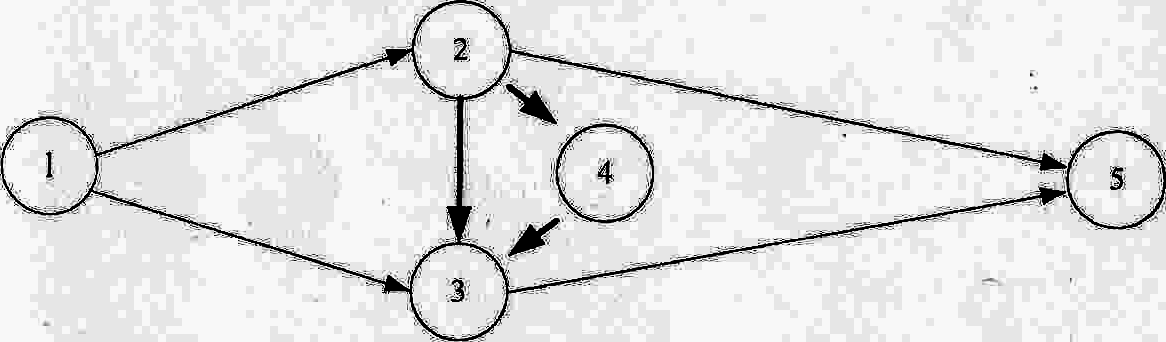
В сетевых графиках этого типа каждая работа находится между двумя событиями: начальным, из которого она выходит, и конечным, в которое она входит. События сетевого графика нумеруются, поэтому каждая работа имеет код, состоящий из номеров её начального и конечного события. Например, на рис. 6.2 работы закодированы как (1,2); (2,3); (2,4); (4,5).
Рис.6.2. Сетевой график «вершины — события»
Если событие сетевого графика «вершины-события» не имеет предшествующих работ, то оно является исходным событием этого графика. Следующие непосредственно за ним работы называются исходными. Если событие не имеет последующих работ, то оно является завершающим событием. Входящие в него работы называются завершающими.
Для правильного отображения взаимосвязей между работами необходимо соблюдать следующие основные правила построения сетевого графика «вершины-события»:
1. При изображении одновременно или параллельно выполняемых работ (например, работ «Б» и «В» на рис.6.2) вводятся зависимость (3,4) и дополнительное событие (3).
2. Если для начала работы «Г» необходимо выполнить работы «А» и «Б», а для начала работы «В» – только работу «А», то вводится зависимость и дополнительное событие (рис.6.3.).
Рис.6.3. Изображение зависимости между работами
3. В сетевом графике не д.б. замкнутых контуров (циклов), т.е. цепочки работ, возвращающейся к тому событию, из которого они вышли (рис.6.4).
Рис. 6.4. Пример замкнутого контура (2,4,3,2)
4. В сетевом графике при поточной организации строительства вводятся дополнительные события и зависимости (рис. 6.5.).
Рис. 6 5. Пример изображения потоков однородных работ