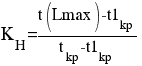Модели сетевого планирования и управления решение задач

РЕШЕНИЕ ЗАДАЧИ МЕТОДАМИ СЕТЕВОГО ПЛАНИРОВАНИЯ И УПРАВЛЕНИЯ

РЕШЕНИИЕ ЗАДАЧИ СЕТЕВОГО ПЛАНИРОВАНИЯ И УПРАВЛЕНИЯ МЕТОДОМ КРИТИЧЕСКОГО ПУТИ

Имеется комплекс работ по переносу участка воздушной высоковольтной линии. Необходимо построить сетевую модель по данным таблицы 2.1, рассчитать временные характеристики сетевого графа, найти время выполнения проекта и критический путь.

Исходным шагом для применения метода CPM является описание проекта в виде перечня выполняемых работ с указанием их взаимосвязи.

Таблица 2.1 Исходные данные задачи

Непосредственно предшествующие работы

A — оценка состава и содержания работ

B — осведомление потребителей электроэнергии о временном отключении системы

C — составление заявки на материалы и оборудование

D — обследование района проведения работ

E — доставка опор и материалов

F — распределение опор по точкам монтажа

H — разметка точек монтажа

K — защита старых проводов

L — протяжка новых проводов

N — выверка провиса новых проводов

P — обесточивание и переключение линий

Q — включение и фазировка новой линии

R — уборка строительного мусора

S — снятие старых проводов

U — доставка неиспользованных материалов на склад

Используя данные таблицы правила построения сети, получаем график.

Рисунок 2.1 — Сетевая модель переноса участка воздушной высоковольтной линии

Определим временные характеристики событий и критический путь для сетевого графика. При определении ранних сроков свершения событий t_р(i) продвигаемся в сетевом графике слева направо, и используем формулу (1.1). Самое раннее время свершения начального события (i=1) t_р(1) = 0, для i = 2 раннее время свершения события t_р(2) = t_р(1) + t(1,2) = 0 + 2 = 2 ед. времени. Аналогично определяются ранние сроки свершения и для других событий сетевого графика.

Длина критического пути равна раннему сроку свершения завершающего события, т.е. 35 ед. времени.

При определении поздних сроков свершения событий t_п(i) продвигаемся в сетевом графике в обратном направлении, т.е. справа налево. Для i = 18 (завершающее событие) поздний срок свершения события должен равняться ее раннему сроку (иначе изменится длина критического пути): t_п(18) = t_р(18) = 35 ед. времени. Для i = 17 t_п(17) = t_п(18) — t(17, 18) = 31 ед. времени. Аналогично по формуле (1.2) определяются поздние сроки свершения и для других событий сетевого графика.

По формуле (1.3) определяются резервы времени i -го события: R(1) = 0; R(2) = 2 — 2 =0; R(3) = 9 -3 = 6 и т.д.

Таблица 2.2 Временные характеристики событий сетевого графика

Ранний срок свершения события t_р(i)

Поздний срок свершения события t_п(i)

Резерв времени i-го события, R(i)

Источник

Примеры решения задач по сетевому планированию

1. Модели сетевого планирования и управления
   Построить график данного комплекса работ.
   Требуется рассчитать:
   • временные характеристики сетевого графика при нормальном режиме работ;
   • найти критический путь;
   • полные резервы времени;
   • временные характеристики сетевого графика при срочном режиме работ;
   • найти критический путь;
   • полные резервы времени;
   • определить стоимость работ.
2. Табличный метод расчета параметров сетевого графика
   Определить временные параметры сетевого графика на рисунке, пользуясь табличным методом.
3. Графический метод расчета параметров сетевого графика
4. Расчет параметров сетевого графика методом потенциалов.
5. Различные варианты анализа сетевых графиков
   Имеются данные о возможности сокращения продолжительности работы за счет стимулирования труда и увеличения других затрат. На основе статистических характеристик проводится анализ сетевой модели.
6. Оптимизация сетевой модели комплекса производственных работ
7. Построение сетевого графика по таблице
   Рассчитать параметры сетевого графика мероприятия по совершенствованию системы управления. Сетевая модель задана таблично (Таблица). Продолжительность выполнения работ дана в виде минимальной и максимальной оценок. Требуется:
   • Вычислить табличным методом все основные характеристики работ и событий, найти критический путь и его продолжительность.
   • Построить масштабный сетевой график.
   • Оценить вероятность выполнения всего комплекса работ за 30 дней.
   • Оценить максимально возможный срок выполнения всего комплекса работ с вероятностью 95%.
8. Коэффициент сложности сетевого графика
9. Коэффициент напряженности.
10. Как решать, если задана стоимость работ?
    По данным таблицы необходимо: 1) построить сетевой график; 2) определить критический путь и стоимость проекта при минимально возможных значениях продолжительности всех работ; 3) найти минимальную стоимость проекта при том же сроке его завершения; 4) рассчитать и построить оптимальную зависимость стоимости проекта от продолжительности его выполнения, используя в качестве первоначального варианта сетевого графика.

Правила ввода данных

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus .
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Поиск

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus .
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Источник

Задачи сетевого планирования

На этой странице вы найдете решенные типовые задания из контрольных по сетевому планированию — разделу экономико-математических методов и моделей.

В рамках изучения сетевого анализа студенты обычно учатся: строить график сети по табличному или словесному описанию проекта (и наоборот), находить ранние и поздние сроки начала и окончания работ, резервы, критический путь и минимальное времеия завершения проекта. Более сложные задания подразумевают различные варианты корректировки и оптимизации сетевого графика (с увеличением времени и уменьшением затрат, или наоборот, с уменьшением времени и увеличением расходов), задачи распределения ресурсов. Изучаются различные графические способы отображения как сетевого графика (см. задачи ниже), так и других диаграмм для проекта (диаграмма Ганта, линейный график).

Примеры решений задач по сетевому планированию онлайн

Задача 1. Для заданной сетевой модели некоторого комплекса работ определить время и критический путь.

Задача 2. Издатель имеет контракт с автором на издание его книги. Ниже представлена последовательность (упрощенная) процессов, приводящая к реализации проекта издания книги. Необходимо разработать сеть для этого проекта.

Задача 3. 1. По заданному перечню работ, построить сетевой график.
2. Определить продолжительности полных путей графика.
3. Определить и выделить критический путь.
4. Определить резерв времени каждого пути.
5. Определить коэффициенты напряженности пути.
6. Определить ранние и поздние сроки начала и окончания работы.
7. Определить полный резерв времени каждой работы.

Задача 4. Рассчитать параметры сетевого графика (см. таблицу работ в файле).

Задача 5. На сетевом графике найти ранние и поздние сроки наступления событий, определить критический путь и резервы времени каждого события.

Задача 6. Построить сетевой график. Решить задачу оптимального распределения ресурсов по работам при постоянных интенсивностях. Наличие ресурса R=10. Работы не допускают перерыва в их выполнении.

Задача 7. По данным варианта требуется:
1) построить сетевую модель;
2) определить критические пути модели;
3) провести максимально возможное уменьшение сроков выполнения проекта при минимально возможных дополнительных затратах

Источник

3. Пример решения задачи методом сетевого планирования и управления

3.1.Постановка задачи и построение сетевого графика

Издатель имеет контракт с автором на издание его книги. Ниже представлена последовательность (упрощенная) процессов, приводящая к реализации проекта издания книги. Необходимо разработать сеть для этого проекта.

А: Прочтение рукописи редактором

В: Пробная верстка отдельных страниц книги

С: Разработка обложки книги

Е: Просмотр автором редакторских правок и сверстанных страниц

F: Верстка книги (создание макета книги)

G: Проверка автором макета книги

H: Проверка автором иллюстраций

I: Подготовка печатных форм

J:Печать и брошюровка книги

На рис.3.1 показана сеть, представляющая взаимосвязь процессов данного проекта. Фиктивный процесс (2, 3) введен для того, чтобы «развести» конкурирующие процессы А и В. Номера узлов сети возрастают в направлении выполнения проектов.

3.2.Расчет параметров сетевого графика

Определение полных путей и нахождение критического пути.

Найдем полные пути и их продолжительности:

1 путь: 1-2-3-4-6-7-8-9, его продолжительность: 3+0+2+2+2+2+4=15

2 путь: 1-3-4-6-7-8-9, его продолжительность: 2+2+2+2+2+4=14

3 путь: 1-5-7-8-9, его продолжительность: 3+1+2+4=10

4 путь: 1-8-9, его продолжительность: 4+4=8

Критическимв данном случае будет путь 1-2-3-4-6-7-8-9, т.к. его продолжительность максимальна и равна 15. Lкр = 1-2-3-4-6-7-8-9,t(Lкр) = 15.

Для каждого события определим ранний и поздний срок свершения события.

Ранний срок свершения события– это максимальный из путей, предшествующий этому событию.

Поздний срок свершения свершения события Тп(i) определяется разностью между Ткр и длинной максимального из последующих путей.

Резерв времени события равен разности раннего и позднего срока свершения события: R(i) = Тп(i)-Тр(i)

Определяем ранние и поздние сроки начала и окончания работ:

Определяем ранний срок начала работ:

Трн( i, j) = Тр(i)

Определяем ранний срок окончания работ:

Тро( i, j) = Тр(i) + Тij

Тро(8, 9) = Тр(8) + Т89 = 11+4 = 15

Определяем поздний срок начала работ:

Тпн(i, j) = Тп(j) – Тij

Тпн(1, 5) = Тп(5) – Т 15= 13-3 = 10

Тпн(1, 8) = Тп(8) – Т18 = 16-4 = 12

Тпн(4, 6) = Тп(6) – Т 46= 12-2 = 10

Тпн(6, 7) = Тп(7) – Т67 = 14-2 = 12

Тпн(5, 7) = Тп(7) – Т57 = 14-1 = 13

Тпн(7, 8) = Тп(8) – Т 78= 16-2 = 14

Тпн(8, 9) = Тп(9) – Т89 = 20-4 = 16

Определяем поздний срок окончания работ:

Тпо(i, j) = Тп(j)

Определяем полный резерв времени работ:

R(i, j) = Tп(j) – Tp(i) – Tij

R(1, 2) = Тп(2) – Тр(1) – Т12 = 8-0-3 = 5

R(1, 3) = Тп(3) – Тр(1) – Т13 = 8-0-2 = 6

R(1, 5) = Тп(5) – Тр(1) – Т15 =13-0-3 = 10

R(1, 8) = Тп(8) – Тр(1) – Т18 =16-0-4 =12

R(2, 3) = Тп(3) – Тр(2) – Т23 = 8-3-0 = 5

R(3, 4) = Тп(4) – Тр(3) – Т34 =10-3-2 = 5

R(4, 6) = Тп(6) – Тр(4) – Т46 =12-5-2 = 5

R(6, 7) = Тп(7) – Тр(6) – Т67 =14-7-2 = 5

R(5, 7) = Тп(7) – Тр(5) – Т57 =14-3-1 = 10

R(7, 8) = Тп(8) – Тр(7) – Т78 =16-9-2 = 5

R(8, 9) = Тп(9) – Тр(8) – Т89 =20-11-4 = 5

Источник