Моделирование в компьютерных сетях и системах

Содержание

Моделирование компьютерных сетей учебно-методическое пособие
Оглавление
1. Моделирование сетей связи, задачи моделирования, виды моделей. Математические модели сетей связи: назначение, области применения (предметная область).
Структура сети связи
2. Сеть связи как система массового обслуживания. Основные процессы в сети связи, показатели (параметры) функционирования сети связи.
40. Имитационное моделирование компьютерных сетей.
41. Имитационное моделирование нейронных сетей.
42. Вероятностно-статистическое моделирование. Метод Монте-Карло.

Моделирование компьютерных сетей учебно-методическое пособие

А.Н. Егоров и др.Моделирование компьютерных сетей: учебно-методическое пособие / А.Н. Егоров, А.Е. Журавлев, А.А. Базунов, О.В Румянцев — СПб.: Изд-во ГУМРФ имени адмирала С. О. Макарова, 2015. — 191с.

В учебно-методическом пособии рассматриваются основные методы проектирования и моделирования компьютерных сетей, в которых используется оборудование Cisco Systems. Детально описываются процессы построения локальных и глобальных корпоративных сетей, приводятся типовые конфигурации коммутаторов и маршрутизаторов Cisco. В качестве среды разработки используется учебная версия программы Cisco Packet Tracer 6, которая является сложной средой симуляции, визуализации и оценки компьютерных сетей уровня CCNA.

Учебное пособие предназначено для студентов второго и третьего курсов, обучающихся по направлениям 230700.62 «Прикладная информатика» и 230400.62 «Информационные системы и технологии» и изучающих курсы компьютерных сетей и инфокоммуникационных систем в качестве основной литературы. Учебно-методическое пособие также может быть использовано студентами, аспирантами и преподавателями в ходе подготовки к экзамену для получения профессиональной сертификации CiscoCCNA.

1. Моделирование сетей связи, задачи моделирования, виды моделей. Математические модели сетей связи: назначение, области применения (предметная область).

Модель – это описание основных характеристик (качеств и функций) объекта.

Моделирование – способ исследования свойств (получения знаний) об объекте: аналитическое / имитационное.

Любая модель обладает следующими свойствами:

Конечностью: модель отображает оригинал лишь в конечном числе его отношений;
Упрощенностью: модель отображает только существенные стороны объекта;
Приблизительностью: действительность отображается моделью грубо или приблизительно;
Адекватностью: модель успешно описывает моделируемую систему;
Информативностью: модель должна содержать достаточную информацию о системе в рамках гипотез.

Основная задача моделирования – описание свойств сетей связи и их элементов.Области применения:

Развитие технологий связи и услуг;
Качество обслуживания трафика (предоставления услуг);
Надежность сети связи (доступность услуг связи);
Экономические показатели.

Состав сети связи:

Узлы сети (УС)
Линии связи (ЛС)

Структура сети связи

Разделение каналов
Пространственное	Использование многопарного кабеля
Частотное [аналоговый сигнал]	Канал делится на различные диапазоны полосы пропускания (каналы).
Временное (формирование Импульсно-Кодовой Модуляции) [аналоговый сигнал, цифровой сигнал]	Разделение времени посредством использования временных интервалов для сигналов

Специфика сетей связи:

Значительные масштабы исследуемой сиcтемы;
Изменение свойств системы в процессе развития;
Случайные процессы при функционировании;
Использование различных технологии реализации услуг…

2. Сеть связи как система массового обслуживания. Основные процессы в сети связи, показатели (параметры) функционирования сети связи.

Сеть связи выполняет работу по обслуживанию трафика. Трафик в сети связи представляет собой процесс поступления и обслуживания заявок пользователей. Процесс поступления заявок, чаще всего, представляет собой случайный процесс. Заявки (вызовы или пакеты данных) поступают в случайные моменты времени. Для обслуживания каждой заявки сеть предоставляет некоторый ресурс, если в момент поступления заявки свободных ресурсов нет, то в зависимости от дисциплины обслуживания, заявка получает либо отказ в обслуживании, либо ставится на ожидание (в очередь). Сеть связи и ее элементы могут быть представлены как системы массового обслуживания (СМО). Функционирование СМО характеризуется параметрами трафика, параметрами пропускной способности и параметрами качества обслуживания. Система массового обслуживания (СМО) – математический (абстрактный) объект, содержащий один или несколько приборов П (каналов), обслуживающих заявки З, поступающие в систему, и накопитель Н, в котором находятся заявки, образующие очередь О и ожидающие обслуживания. 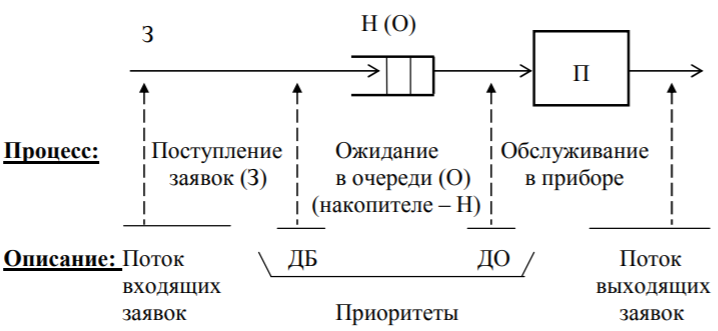Дисциплина буферизации (ДБ) – правило занесения поступающих заявок в накопитель (буфер). Дисциплина обслуживания (ДО) – правило выбора заявок из очереди для обслуживания в приборе. Основная задача моделирования сети связи – определить соотношение между трафиком, ресурсами сети и качеством обслуживания QoS (Quality of Service).

Параметры функционирования и параметры надежности

Источник

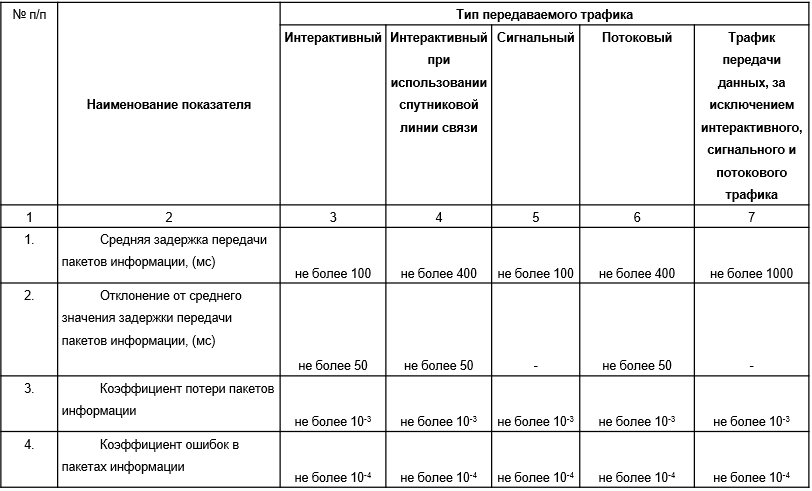40. Имитационное моделирование компьютерных сетей.

Эффективность построения и использования корпоративных информационных систем стала чрезвычайно актуальной задачей, особенно в условиях недостаточного финансирования информационных технологий на предприятиях.

Критериями оценки эффективности могут служить снижение стоимости реализации информационной системы, соответствие текущим требованиям и требованиям ближайшего времени, возможность и стоимость дальнейшего развития и перехода к новым технологиям.

Основу информационной системы составляет вычислительная система, включающая такие компоненты, как кабельная сеть и активное сетевое оборудование, компьютерное и периферийное оборудование, оборудование хранения данных (библиотеки), системное программное обеспечение (операционные системы, системы управления базами данных), специальное ПО (системы мониторинга и управления сетями) и в некоторых случаях прикладное ПО.

Наиболее распространенным подходом к проектированию информационных систем в настоящее время является использование экспертных оценок. В соответствии с этим подходом специалисты в области вычислительных средств, активного сетевого оборудования и кабельных сетей на основании имеющегося у них опыта и экспертных оценок осуществляют проектирование вычислительной системы, обеспечивающей решение конкретной задачи или класса задач.

Этот подход позволяет минимизировать затраты на этапе проектирования, быстро оценить стоимость реализации информационной системы. Однако реш., получ. с исп-ем экспертных оценок, носят субъективный хар-р, требования к оборудованию и программному обеспечению также грешат субъективностью, как и оценка гарантий работоспос-ти и развиваемости предлаг-го проекта сист.

В кач. альтернативного может быть использован подход, предполаг. разработку модели и моделир-е (имитацию работы — simulation) поведения вычислит. сист.

41. Имитационное моделирование нейронных сетей.

42. Вероятностно-статистическое моделирование. Метод Монте-Карло.

Мод-е по методу МК определяется как процедура, в кот. исп-ся случ. числа, т.е. случ. велич.(СВ) U(0,1). Такая процедура предназнач. для реш. стохастич. и детерминистич. задач, в кот. течение времени не играет особой роли. След-но мод-е по методу МК явл. скорее статич., чем динамич., хотя применим к любому типу модел-я, в кот. исп-ся случ. числа.

Пусть необх. оценить интеграл , гдеявл-ся действит. ф-цией, к-рую нельзя интегрировать аналитически. Рассмотрим, как детерминистич. задача м/б решена с пом. метода МК. ПустьY будет СВ (b—a)g(X), где X – непрер. СВ, распред. равномерно между [a,b]. Тогда мат. ожид. значения Y:

где – плотность распред-я вер-тей СВU(a,b). Т. о., задача оценки интеграла упрощена до оценки ожидаемой величины E(Y).

В наст. время мод-е по методу МК широко примен. при реш. определ. задач стат-ки, кот. не поддаются аналитич. обработке. Этот тип мод-я примен. для оценки критич. знач. или достоверности критерия при проверке гипотезы.

Метод Монте-Карло. Область применения метода.

В осн лежит моделирование статистического эксперимента с пом-ю ср-в вычислительной техники и регистрация числовых характ-к, получаемых из этого эксперимента. Поэтому все эти методы объединяются под общим названием метода стат испытаний или метода Монте-Карло. Решение численных задач этим методом по духу своему ближе к физическому эксперименту, чем к классическим численным методам.

Ошибка метода МК не может быть дост-но хорошо оценена заранее и, как правило, находится путем опр-ния средних квадратичных для моделируемых величин. Решение не мб в ряде случаев в точности воспроизведено. Решение устойчиво по отношению к единичным ошибкам в работе используемой вычислительной машины.

Метод МК находит применения в чисто мат выч-ных задачах и осн область применения метода — вычисление многомерных интегралов.

Особенно широко и успешно используется метод МК во многих областях физики и техники. Это обусловлено тем, что в них иссл-ся случайные процессы настолько сложные, что их аналитическое описание практически невозм. Однако статистическое моделирование таких процессов в цифровых вычислительных машинах позволяет с успехом проводить иссл-ние.

Так же находит применение метод МК в исследовании процессов массового обслуживания. Иногда исходной является аналитическая постановка задачи (например, краевая задача для уравнения Лапласа), затем нах-ся случайный процесс (например, процесс блужданий) и изучается этот процесс. В других случаях исх явлся задание некот случайного процесса, аналитическое описание кот практически бесполезно или вообще никогда не рассм-ся. Сюда относится, н-р, определение парам-в некот процесса массового обслуживания.

В действ-ти чаще приходится некот изучаемому процессу ставить в соотв-е упрощенный искусственный процесс, моделируемый в выч машине и в некот смысле приближающий исх процесс.

Наиб-шие успехи метод Монте-Карло принес в тех областях, где основная мат задача состоит в иссл-ии того или иного случайного процесса. Однако существуют вычислительные задачи, которые в своей постановке не связаны с теорией вер-тей, но к кот хорошо применим метод МК. Н-р: краевые задачи для эллиптических уравнений (н-р, для ур-я Лапласа) и родственные им задачи для параболических ур-ий (ур-е теплопроводности).

Решения этих ур-ий тесно связаны с характеристиками некот случайных процессов диффузионного типа. Поэтому решение этих ур-й удобно сводится к моделированию таких процессов. Интересно отметить, что когда связь между краевыми задачами и случайными процессами была впервые отмечена, то основной интерес к этому факту состоял в том, что возможно было применить методы теории дифференциальных ур-й к иссл-ю широкого класса случайных процессов. В методе МК эта классическая ситуация оказалась обращенной в противоположную сторону. Именно, здесь моделирование случайных процессов оказывается очень удобным методом для фактического нахождения решений дифференциального ур-я.