Некоторый сегмент сети интернет сомики

Некоторый сегмент сети интернет сомики

Ключевое слово Количество сайтов, для которых данное слово
является ключевым

некоторый сегмент сети интернет состоит из 1000 сайтов поисковый сервер
в автоматическом режиме составил таблицу ключевых слов для этого сегмента вот её фрагмент ( дан вверху)
по запросу сомики 8 гуппи было найдено 0 сайтов, по запросу сомики 8 меченосцы- 20 сайтов, а по запросу меченосцы 8 гуппи — 10 сайтов сколько сайтов будет найдено по запросу сомики I меченосцы I гуппи
для скольких сайтов рассматриваемого сегмента ложно высказывание сомики —
ключевое слово сайта ИЛИ меченосцы — ключевое слово сайта ИЛИ гуппи — ключевое слово сайта

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

• bookmark_border

• 17.05.2015 22:38
• Информатика
• remove_red_eye 16547
• thumb_up 10

Ответы и объяснения 1

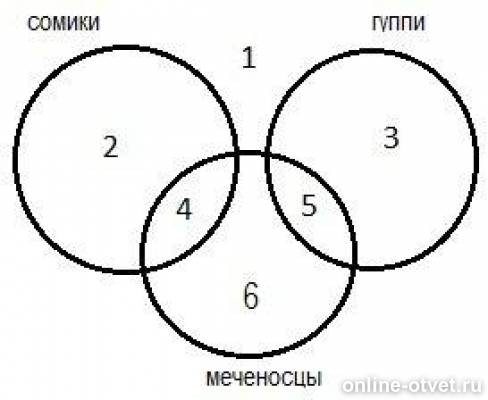
Задачу удобно решать с помощью кругов Эйлера (см. рис.).
K1+K2+K3+K4+K5+K6 = 1000
K2+K4 = 250
K4+K5+K6 = 200
K3+K5 = 500
K4 = 20
K5 = 10
K2+K3+K4+K5+K6 — ?
K1 — ?

K2+K3+K4+K5+K6 = (K2+K4)+(K4+K5+K6)+(K3+K5)-K4-K5 = 250+200+500-20-10 = 920
K1 = (K1+K2+K3+K4+K5+K6)-(K2+K3+K4+K5+K6) = 1000-920 = 80

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Информатика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Информатика — наука о методах и процессах сбора, хранения, обработки, передачи, анализа и оценки информации с применением компьютерных технологий, обеспечивающих возможность её использования для принятия решений.

Источник

Некоторый сегмент сети интернет сомики

Задание №3100.
Принципы поиска информации в Интернете. ОГЭ по информатике

Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот её фрагмент.

Ключевое слово	Количество сайтов, для которых данное слово является ключевым
Сомики	250
Меченосцы	200
Гуппи	500

Сколько сайтов будет найдено по запросу (Сомики & Меченосцы) | Гуппи, если по запросу Сомики & Меченосцы было найдено 100 сайтов; по запросу Сомики | Гуппи – 750 сайтов; по запросу Меченосцы & Гуппи – 0 сайтов?

Для обозначения логической операции «ИЛИ» в запросах используется символ «|», а для обозначения логической операции «И» – символ «&».

Пояснение:
600 — столько сайтов будет найдено по запросу (Сомики & Меченосцы) | Гуппи, если по запросу Сомики & Меченосцы было найдено 100 сайтов; по запросу Сомики | Гуппи – 750 сайтов; по запросу Меченосцы & Гуппи – 0 сайтов.

Показать ответ
600

Источник: ФИПИ. Открытый банк тестовых заданий
Сообщить об ошибке

Источник

ОГЭ — 2022, задание 8. Логика. Запросы для поисковых систем с использованием логических выражений, тест 3

Презентация — тест «Математическая логика. Запросы для поисковых систем с использованием логических выражений», 8 — 9 классы, тест 3 по сути является практической работой для подготовке к ОГЭ — 2022, задание 8 (решения и ответы даются в презентации при клике мышкой). Цель создания — в блоге «Презентации: тесты — зачем они нужны и где могут пригодиться»

Просмотр содержимого документа
«ОГЭ — 2022, задание 8. Логика. Запросы для поисковых систем с использованием логических выражений, тест 3»

Запросы для поисковых систем с использованием логических выражений Тест 3

Учебная презентация по информатике (8-9 класс)

Автор: Звездина Вера Алексеевна ,

МБОУ го. Ивантеевка Московской области

«Средняя общеобразовательная школа №7»

Математическая логика, тест 3, теория

При выполнении данного задания

множество точек пересечения И попадает в область ИЛИ два раза (как

в А , так и в В ). Тогда ИЛИ = А + В – И ,

а И = А + В – ИЛИ ,

Математическая логика, тест 3, теория

Если множеств более двух, то нужно сложить значения всех множеств и вычесть все их объединения (если считаем И ) или пересечения (при подсчете ИЛИ ), то есть для трех множеств получим

A | B | C = A + B + C — A & B & C,

A & B & C = A + B + C – A | B | C

При возникновении трудностей

в решении задания следует нарисовать кольца Эйлера, обозначить на них все полученные в задании значения — и все станет понятнее!

Математическая логика, тест 3, задача 1

Некоторый сегмент сети Интернет состоит из

1000 сайтов. Поисковый сервер в автоматическом

режиме составил таблицу ключевых слов для

сайтов этого сегмента. Вот ее фрагмент:

Математическая логика, тест 3, задача 1

Сколько сайтов будет найдено по запросу

сомики | меченосцы | гуппи

если по запросу сомики & гуппи было найдено

0 сайтов , по запросу сомики & меченосцы – 20 , а по запросу меченосцы & гуппи – 10 ?

С | М | Г = С + М + Г – С & М – С & Г – М & Г =

= 250 + 200 + 500 – 20 – 0 – 10 = 920

Математическая логика, тест 3, задача 2

Некоторый сегмент сети Интернет состоит из

1000 сайтов. Поисковый сервер в автоматическом

режиме составил таблицу ключевых слов для

сайтов этого сегмента. Вот ее фрагмент:

Математическая логика, тест 3, задача 2

Сколько сайтов будет найдено по запросу

(сомики & меченосцы) | гуппи

если по запросу сомики | гуппи было найдено 750 сайтов , по запросу сомики & меченосцы – 100 , а по запросу меченосцы & гуппи – 0 ?

Так как гуппи не пересекаются с другими множествами (М & Г = 0 по условию, а

С & Г = С + Г – С | Г = 250 + 500 — 750= 0), тогда

(сомики & меченосцы) | гуппи = 100 + 500 = 600

Математическая логика, тест 3, задача 3

Некоторый сегмент сети Интернет состоит из

1000 сайтов. Поисковый сервер в автоматическом

режиме составил таблицу ключевых слов для

сайтов этого сегмента. Вот ее фрагмент:

Математическая логика, тест 3, задача 3

Сколько сайтов будет найдено по запросу

принтер | сканер | монитор

если по запросу принтер | сканер было найдено 450 сайтов, по запросу принтер & монитор – 40,

а по запросу сканер & монитор – 50?

Согласно условию, П + С = 200 + 250 = 450 = П | C,

то П & C = 0 (не пересекаются).

Тогда П | С | М = 200 + 250 + 400 – 40 — 50 – 0 = 810

Математическая логика, тест 3, задача 4

В таблице приведены запросы и количество

страниц, которые нашел поисковый сервер по

этим запросам в некотором сегменте Интернета:

Сколько страниц (в тысячах) будет найдено по

запросу фрегат & эсминец ?

Ф & Э = Ф + Э – Ф | Э = 2000 + 2500 – 3000 = 1500

Математическая логика, тест 3, задача 5

В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

Сколько страниц (в тысячах) будет найдено

по запросу фрегат | эсминец ?

Ф | Э = Ф + Э – Ф & Э = 2000 + 2500 – 500 = 4000

Математическая логика, тест 3, задача 6

В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

Сколько страниц (в тысячах) будет найдено

Ф = Ф & Э – Э + Ф | Э = 500 – 2500 + 4500 = 2500

Математическая логика, тест 3, задача 7

В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

Сколько страниц (в тысячах) будет найдено

по запросу крейсер & линкор ?

К & Л = К + Л – К | Л = 4800 + 4500 – 7000 = 2300

Математическая логика, тест 3, задача 8

В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

Сколько страниц (в тысячах) будет найдено

Т = Т & П – П + Т | П = 6500-7700+12000 = 10800

Математическая логика, тест 3, задача 9

В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

Сколько страниц (в тысячах) будет найдено

по запросу ландыши & васильки & лютики ?

Л & B & Л = 650 + 230 – 740 = 140

Математическая логика, тест 3, задача 10

Некоторый сегмент сети Интернет состоит из 5000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:

Математическая логика, тест 3, задача 10

Сколько сайтов будет найдено по запросу

(принтеры | мониторы) & сканеры

если по запросу принтеры | сканеры было найдено 600 сайтов , по запросу принтеры | мониторы – 900, а по запросу сканеры | мониторы – 750 ?

Тогда (П|М)& С =(П&С) | (М&С) = 100+50=150

Источник