Нумерация событий сетевой модели

Нумерация событий сетевой модели: ПРАВИЛО ВЫЧЁРКИВАНИЯ ДУГ (РАБОТ) — презентация

• 

Первый слайд презентации: Нумерация событий сетевой модели: ПРАВИЛО ВЫЧЁРКИВАНИЯ ДУГ (РАБОТ)

Слайд 2

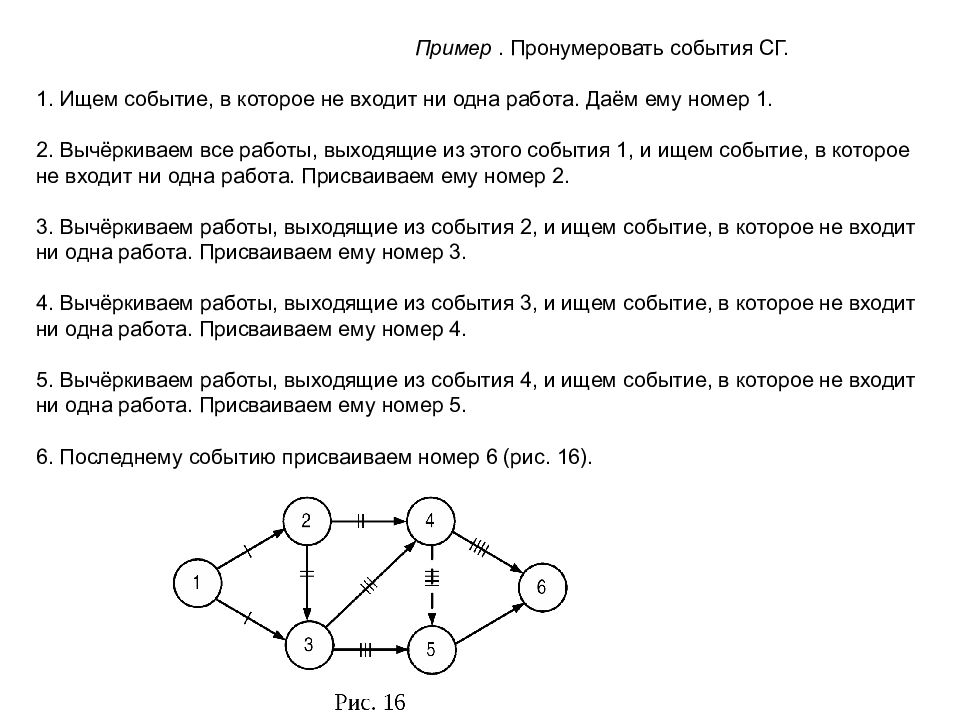
П ример. Пронумеровать события СГ. 1. Ищем событие, в которое не входит ни одна работа. Даём ему номер 1. 2. Вычёркиваем все работы, выходящие из этого события 1, и ищем событие, в которое не входит ни одна работа. Присваиваем ему номер 2. 3. Вычёркиваем работы, выходящие из события 2, и ищем событие, в которое не входит ни одна работа. Присваиваем ему номер 3. 4. Вычёркиваем работы, выходящие из события 3, и ищем событие, в которое не входит ни одна работа. Присваиваем ему номер 4. 5. Вычёркиваем работы, выходящие из события 4, и ищем событие, в которое не входит ни одна работа. Присваиваем ему номер 5. 6. Последнему событию присваиваем номер 6 (рис. 16).

Слайд 3

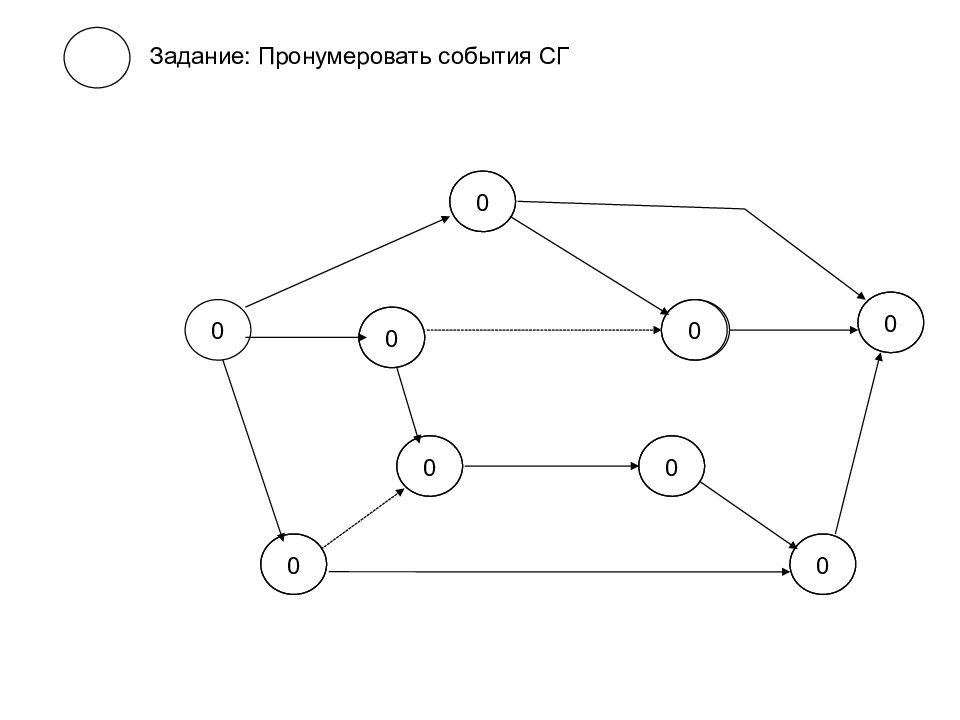
Задание: Пронумеровать события СГ 0 0 0 0 0 0 0 0 0

Слайд 4: Определение времени выполнения работ в сетевом графике

Могут быть даны следующие оценки времени: t min — минимальная (оптимистическая) оценка — время, необходимое для выполнения работы при наиболее благоприятном стечении обстоятельств; t max — максимальная (пессимистическая) оценка — время, необходимое для выполнения работы при самых неблагоприятных обстоятельствах; t н.в. — наиболее вероятная продолжительность работ — продолжительность, имеющая место при нормальных, чаще всего встречающихся условиях выполнения данной работы.

Слайд 5: Определение последовательности операций. Сетевой график

№ операции Операция Преды- дущие Продолжи- тельность, неделя 1 Подписание контракта Нет 1 2 Регистрация юридического лица 1 4 3 Поиск помещения 1 2 4 Найм персонала 1 1 5. Аренда помещения 2,3 1 6 Закупка и поставка оборудования 2(1) 8 7 Обучение персонала 4 1 8 Ремонт помещения 5 4 9 Монтаж оборудования 6,8 1 10 Запуск оборудования 7,9 1 Пример. Организация производства инновационной продукции Длина критического пути – 15 недель 4 1 7 1 10 1 1 1 2 4 6 8 9 1 3 2 5 1 8 4 Сетевая диаграмма проекта

Источник

21. Правила нумерации событий.

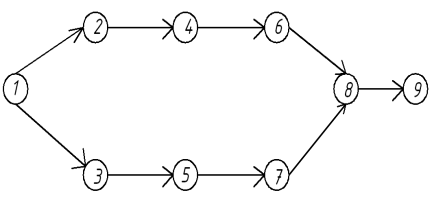
Нумерация событий производится при построенном сетевом графике в соответствии с последовательностью работ во времени по горизонтальной или вертикальной схеме. При горизонтальной схеме события кодируются слева направо по прямым до первого пересечения работ, а при вертикальной схеме нумерацию начинают сверху вниз и снизу вверх с учетом того, что каждое последующее событие получило номер после предыдущего.

22. Порядок разработки сетевых графиков.

Перед началом работ сетевого графика надо изучить технологию производства работ и организацию строительства. Каждый объект имеет свои особенности и их следует учитывать при построении модели. Для разработки сетевого графика готовят исходные данные: 1) рабочие чертежи; 2) технологические карты; 3) сметы; 4) проекты организации строительства; 5) данные о поставках материальных ресурсов, оборудов., типах машин, механизмов; 6) нормативная документация; 7) калькуляция трудовых затрат и ЗП. После подготовки исходных данных заполняют карточку-определитель работ сетевого графика – исходный документ для построения модели. Заполнение этой карточки осущ-ся параллельно с разработкой модели сетевого графика. Порядок заполнения карточки-определителя: 1) заполняются гр.1,2 на основании ведомости затрат труда и маш. времени; 2) заполняются гр.5,6,9,12,13,15; 3) по ведущему процессу в составе труд-ти планируют продолжительность, сменность и кол-во раб. смен, т.е. заполн. гр.10,8,11; 4) строим сетевой график. Общая структура сетевого графика должна отображать технолог-ую связь работы. График строится безмасштабно, но в строгой технолог-ой последовательности. Все работы, имеющиеся в карточке-определителе должны быть в сетевом графике. После разработки графика и его проверки задают характеристику работам и производят расчёт одним из методов. На основе расчётов параметров сетевого графика рассчитывают резервное время, выявляют критический путь и производят его корректировку (если надо). Полученный график является первичным. При необходимости производят сшивание сетевых графиков, т.е. укрупнение с соблюдением правил. В дальнейшем строят эпюры потребности материально-технических ресурсов.

23. Расчёт ранних сроков начала и окончания работ и их содержание.

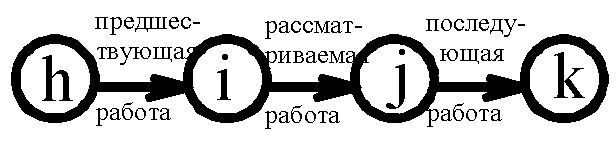
i-j=код рассматриваемой работы; i=код начального события; j=код конечного события; h-i,j-k=коды предшествующей и последующей работы; h=код исходного события; k= код завершающего события; t_i-j=продолжительность рассматр-ой работы; t_i-j рн =раннее начало рассматр-ой работы; t_i-j пн =позднее начало рассматр-ой работы; t_i-j ро =ранее окончание рассматриваемой работы; t_i-j по =позднее окончание рассматриваемой работы; Т_кр=продолжительность критического пути; Р_i—j=общий резерв времени; r_i—j=частный резерв времени. Ранний срок начала работы t_i-j рн – это самое раннее из возможного времени, в которое можно начать работу с учетом сроков выполнения всех предшествующих работ: t_i-j рн = мах t_h—i. Раннее начало работы определяется продолжительностью самого длинного пути от исходного события до начала данной работы. Раннее начало всех работ, выходящих из исходного события равно нулю: t_h—i рн =о. Все работы, выходящие из одного события имеют одинаковое раннее начало: t_h-i1 рн = t_h-i2- рн и так далее по всем работам h-i. Раннее окончание работы t_i-j ро – это время окончания работы, если она была начата в самый ранний из возможных сроков. Она равна сумме раннего начала данной работы и ее продолжительности, т.е t_i-j ро = t_i-j рн + t_i—j. Раннее окончание предшествующей работы является ранним началом последующей работы. Если одним событием заканчивается несколько работ, то раннее начало работы, выходящее из этого события равно максимальному из величин ранних окончаний этих работ: mах t ро _{(h—i),(h 1-i),(h2-i) =} t рн _i—k. Если событие является началом двух работ и более, то ранние сроки работ эитх работ равны между собой и равны раннему окончанию предшествующей работы: t_h—i ро = t_i—j рн = t_i—J рн . Раннее окончание работы входящей в завершающее событие равно продолжительности критического пути: t_i-k ро = T_кр. Если в завершающее событие входит две и более работы, то максимальная из величин ранних окончаний работ будет равна критическому пути и определит самый поздний срок окончания всех работ входящих в конечное событие: Т_кр = max t_j-k ро .

Источник

Правила нумерации событий сетевого графика (показать на примере)

Нумерация события начинается с исходного события, которому присваивается номер 0 или 1.

После нумерации исходного события, а затем и следующих, получившие номера, вычёркиваются все работы, выходящие из этого события.

Следующим нумеруются события, в которые входят вычеркнутые работы. Если все вычеркнутые работы входят два и более событий, порядок нумерации устанавливает пользователь.

Последним нумеруется завершающее событие, в которое входят вычеркнутые работы.

Цель расчёта сетевого графика. Общая характеристика основных этапов расчёта.

Цель расчёта сетевого графика состоит в том, чтобы определить время, за которое будет выполнен планируемый комплекс работ.

Основными этапами расчёта являются:

Расчёт событий начинается с расчёта ранних сроков выполнения работ.

После определения ранних сроков определяются поздние сроки выполнения работ

После вычисления ранних и поздних сроков события вычисляется резерв сроков событий.

Расчёт временных характеристик работ. При расчёте временных характеристик работ преследуются 3 цели:

• определение прохождения критического пути
• определение резервов времени работ, для последующего их использования при возможном улучшении (оптимизации) сетевого графика.
• определение временных характеристик работ, которые будут использоваться в процессе выполнения комплекса работ для анализа состояния выполнения этих работ – допустимое время

Понятие пути в сетевом графике. Временные характеристики путей. Виды путей. Критический путь, его сущность.

Под путём в сетевом графике понимается перечень работ, связывающих одно событие с другим. Пути бывают полными, неполными, критическими. Критический путь понимается как полный путь (путь от исходного события до завершающего), имеющий наибольшую продолжительность. Таких путей может быть несколько.

Сущность критического пути заключается в том, что он определяет продолжительность промежутка времени, за который будет выполнен анализируемый комплекс работ.

Временными характеристиками пути являются его продолжительность, резерв времени

Расчёт событий. Понятие, назначение и общая характеристика элементов, определяемых при расчёте событий.

При расчёте событий определяются 3 основных элемента:

• ранние сроки выполнения работ, ранний срок наступления события определяется тем временем, раньше которого это событие не может произойти. Расчёт ранних сроков наступления события начинается с исходного события, для которого ранний срок наступления принимается равным 0. Для всех последующих событий ранний срок вычисляется по следующим двум зависимостям:

а) если в событие входит только одна работа, то ранний срок его наступления

б) В том случае, если в какое-то событие входят несколько работ, то в общем виде расчётная формула имеет вид:

Суть в том, что для каждой входящей в событие работы вычисляется ранний срок наступления события, а затем из всех возможных сроков выбирается максимальный.

Ранний срок завершающего события определяет, какое время будет выполняться комплекс работ

• поздние сроки выполнения работ, расчёт этой характеристики начинается с завершающего события, поздний срок которого принимается равный раннему.
• Затем ведётся от завершающего события к исходному. Поздний срок наступления события характеризует самое позднее возможное время, в которое событие может произойти.

Вычисление поздних сроков наступления событий ведётся по 2м следующим формулам:

t_pi = t_pj – t_ij (3) – используется в том случае, когда пару событий связывает одна работа, и в события больше не входят работы ни от каких событий.

Если же из события выходит несколько работ, то вычисление ведётся по следующей формуле:

Поздний срок наступления исходного события всегда равен нулю!

• резервы времени работ, резерв времени события показывает, на какое предельно допустимое время можно задержать наступление этого события, не вызывая при этом увеличения времени комплекса работ.

Первым показателем определения критического пути является нахождения полного пути, проходящего через те события, резервы времени которых равны нулю.

Источник

2. Правила построения сетевых моделей

В сетевой модели должна отражаться технологическая последовательность и очерёдность отдельных работ. Модель должна иметь простую форму. Стрелки должны быть направлены слева направо от события с меньшим номером к событию с большим номером, необходимо стремиться к минимальному пересечению отдельных работ.

2.1. Основные правила

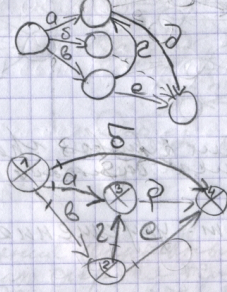
1. Правило составных работ – любая работа а может быть разбита на составляющие, если после частичного выполнения её можно начать следующую работу б. При этом вводятся логические зависимости и дополнительные события (рис. 4).

2. Правило параллельных работ – если между двумя событиями необходимо показать две или несколько работ, которые выполняются параллельно, в модели вводятся дополнительное событие по окончании одной из параллельных работ и логическая зависимость (фиктивная работа) между ними (рис. 5).

3. Правило зависимых и независимых работ – если для начала одной работыг необходимо выполнение всех пред-шествующих работ a и б, а для начала работы в необходимо выполнение только работы a, то вводятся дополнительное событие и логическая зависимость (рис. 6).

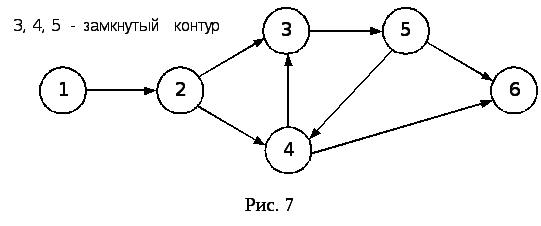
4. Правило запрещения замкнутых контуров, т.е. один путь не должен дважды проходить через одно событие (рис. 7).

5. Правило запрещения тупиковых событий, т.е. событий, из которых не выходит ни одна работа, если событие не завершающее (рис. 8).

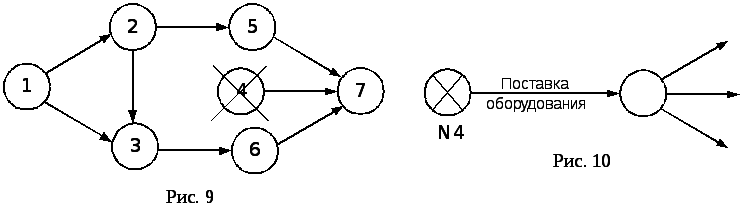
6. Правило запрещения необеспеченных событий, т.е. со- бытий, в которые не входит ни одна работа, если событие не исходное (рис. 9).

7. Правило изображения поставки (рис. 10).

2.2. Построение сетей

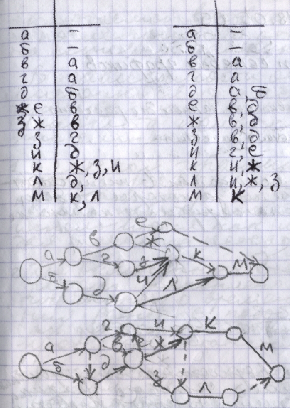
Для построения сетевой модели нужно знать технологию работ и зависимость одних работ от других. Последовательность выполнения работ записывается в форме таблицы, в которой указывается зависимость данной работы ig от предшествующей hi.

Пример 1. По данной зависимости работ построить сетевую модель.

Источник