Правила построения сетевой модели
Правило I. Каждая операция в сети представляется одной и только одной дугой (стрелкой ). Ни одна из операций не должна, появляться в модели дважды. При этом следует различать случай, когда какая-либо операция разбивается на части; тогда каждая часть изображается отдельной дугой. Так, например, прокладку трубопровода можно расчленить на прокладку отдельных секций и рассматривать прокладку каждой секции как самостоятельную
Правило2 . Ни одна пара операций не должна определяться начальным и конечным событиями , Возможность неоднозначного определения операций через события появляется В когда две или больше число операцй допустимо выполнять одновременно. Пример такого случая приведен на рис., 3, где операции А и В имеют одинаковое начальное и конечное события.
Чтобы исключить такую «ошибку» между А и конечным (начальным) событием или между В и конечным (начальным) событием, вводится фиктивная операция. Рис. 4 иллюстрирует различные варианты введения такой фиктивной операции D.В результате операции А и В определяются однозначно парой собьтий, отличающихся либо номером начального, либо номером конечного события. Следует обратить внимание на то, что фиктивные операции не требуют затрат ни времени, ни ресурсов.
Фиктивные операции позволяют также правильно отображать логические связи, которые без их помощи нельзя задать на сети. Предположим, что в некоторой программе операции А и В должны непосредственно предшествовать С , а операции С непосредственно предшествует только В. На рис. 5 эти условия отражены неверно, так как, хотя упорядочения между А , В и С показаны правильно, из этого фрагмента следует, что операции Е должны непосредственно предшествовать обе операции А и В.
Правильное представление указанных условий дает фрагмент, изображенный на рис. 6, в котором используется фиктивная операция D. Поскольку на операцию D не затрачивается ни время, ни ресурсы, заданные отношения упорядочения выполняются.
Правило 3. При включении каждой операции в сетевую модель для обеспечения правильного упорядочения необходимо дать ответ на следующие вопросы :,
а) Какие операции необходимо завершить непосредственно началом рассматриваемой операции ?
б) Какие операции должны непосредственно следовать после завершения данной операции?
в) Какие операции могут выполняться одновременно с рассматриваемой ?
Это правило не требует пояснений. Оно позволяет проверять ( и перепроверять) отношение упорядочения в процессе построения сети.
Пример1. Построить сетевую модель, включающую операции А, В, С,…, L, которая отображает следующие отношения упорядочения:
§ 2. Расчет сетевой модели
Применение методов СПУ в конечном счете должно обеспечить получение календарного плана, определяющего сроки начала и окончания каждой операции. Построение сети является лишь первым шагом на пути к достижению этой цели. Вследствие наличия взаимосвязей между различными операциями для определения сроков их начала и окончания необходимо проведение специальных расчетов. Эти расчеты можно выполнять непосредственно на сети, пользуясь простыми правилами. В результате вычислений определяется критические и некритические операции программы. Операция считается критической, если задержка ее начала приводит к увеличению срока окончания всей программы. Некритическая операция отличается тем, что промежуток времени между ее ранним началом и поздним окончанием (в рамках рассматриваемой программы) больше ее фактической продолжительности. В таком случае говорят, что некритическая операция имеет резерв, или запас времени.
Преимущества, обеспечиваемые за счет выявления критических операция и определения резервов времени, рассматриваются в § 3. В данном параграфе в основном излагаются методы получения этой информации.
1. Сетевая модель и ее основные элементы.
Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ (операций), заданного в специфической форме сети, графическое изображение которой называется сетевым графиком. Отличительной особенностью сетевой модели является четкое определение всех временных взаимосвязей предстоящих работ.
Главными элементами сетевой модели являются событиями и работы
Термин работа используется в СПУ в широком смысле.Во-первых, это действительная работа — протяженный во временипроцесс, требующий затрат ресурсов (например, сборка изделия, испытание прибора и т.п.). Каждая действительная работа, должна быть конкретной, четко описанной и иметь ответственного исполнителя.
Во-вторых, это ожидание — протяженный во времени процесс,не требующий затрат труда (например, процесс сушки после окраски, старения металла, твердения бетона и т.п.).
В-третьих, это зависимость, или фиктивная работа — логическая связь между двумя или несколькими работами (события), не требующими затрат труда, материальных ресурсов или времени. Она указывает, что возможность одной работы непосредственно зависит от результатов другой. Естественно, что продолжительность фиктивной работы принимается равной нулю.
Событие — это момент завершения какого-либо процесса, отражающий отдельный этап выполнения проекта. Событие может являться частным результатом отдельной работы или суммарным результатом нескольких работ. Событие может свершиться только тогда, когда закончатся все работы, ему предшествующие. Последующие работы могут начаться только тогда, когда событие свершится. Отсюда двойственный характер события: для всех непосредственно предшествующих ему работ оно является конечным, а для всех непосредственно следующих за ним — начальным. При этом предполагается, что событие не имеет продолжительности и свершается как бы мгновенно. Поэтому каждое событие, включаемое в сетевую модель, должно быть полно, точно и всесторонне определено, его формулировка должна включать в себя результат всех непосредственно предшествующих ему работ.
Среди событий сетевой модели выделяют исходное и завершающее события. Исходное событие не имеет предшествующих работ и событий, относящихся к представленному в модели комплексу работ. Завершающее событие не имеет последующих работ и событий.
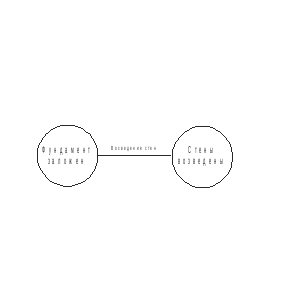
События на сетевом графике (или, как еще говорят, на графе)изображаются кружками (вершинами графа), а работы — стрелками(ориентированными дугами), показывающими связь между работами. Пример фрагмента сетевого графика представлен на рис 1:
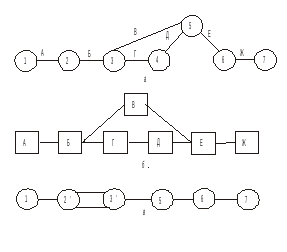
На рис. 2, а приведен сетевой график задачи моделирования и построения оптимального плана некоторого экономического объекта. Чтобы решить эту задачу, необходимо провести следующие работы: А – сформулировать проблему исследования; В5 — математическую модель изучаемого объекта; В — собрать информацию; Г — выбрать метод решения задачи; Д — построить и отладить программу для ЭВМ; Е — рассчитать оптимальный план; Ж — передать результаты расчета заказчику. Цифрами на графике обозначены номера событий, к которым приводит выполнение соответствующих работ.
Из графика, например, следует, что работы В и Г можно начать выполнять независимо одна от другой только после свершения события 3, т.е. когда выполнены работы А и Б; работу Д — после свершения события 4, когда выполнены работы А, Б и Г; а работу Е можно выполнить только после наступления события 5, т.е. при выполнении всех предшествующих ему работ А, Б, В, Г и Д.
В сетевой модели, представленной на рис. 2 а, нет числовых оценок. Такая сеть называется структурной. Однако на практике чаще всего используются сети, в которых заданы оценки продолжительности работ (указываемые в часах, неделях, декадах, месяцах и т.д. над соответствующими стрелками), а также оценки других параметров, например трудоемкости, стоимости и т.п. Именно такие сети мы будем рассматривать в дальнейшем.
Но прежде сделаем следующее замечание. В рассмотренных примерах сетевые графики состояли из работ и событий. Однако может быть и иной принцип построения сетей — без событий. В такой сети вершины графа (например, изображенные прямоугольниками) означают определенные работы, а стрелки — зависимости между этими работами, определяющие порядок их выполнения. В качестве примера сетевой график «события — работы» задачи моделирования и построения оптимального плана некоторого экономического объекта, приведенный на рис. 2 а, представлен в виде сети «работы — связи» на рис. 2 б. А сетевой график «события — работы» той же задачи, но с неудачно составленным перечнем работ, представлен на рис. 2 в (см. правило 3 в разд. 3).
Следует отметить, что сетевой график «работы — связи» в отличие от графика «события — работы» обладает известными преимуществами: не содержит фиктивных работ, имеет более простую технику построения и перестройки, включает только хорошо знакомое исполнителям понятие работы без менее привычного понятия события. Вместе с тем сети без событий оказываются значительно более громоздкими, так как событий обычно значительно меньше, чем работ (показатель сложности сети, равный отношению числа работ к числу событий, как правило, существенно больше единицы). Поэтому эти сети менее эффективны с точки зрения управления комплексом. Этим и объясняется тот факт, что (при отсутствии в целом принципиальных различий между двумя формами представления сети) в настоящее время наибольшее распространение получили сетевые графики «события — работы».