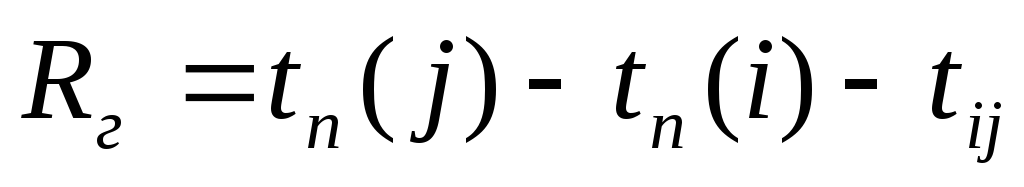33. Определение резервов времени сетевой модели.
Сетевая модель – ориентированный граф изображающий все необходимое, для достиж целей операции в технологич-ой взаимосвязи.
Основные элементы сет модели:
2. Событие- результат выполнения 1 или неск-ких работ, позволяющий начинать след работу, изображ-ся в виде круга.
3. Путь- непрерывная послед-ть работ от исходного до завершающего события сетевой модели.
Если из продолжительности критического пути вычесть продолжительность любого другого пути, то получим общий резерв этого пути, т.е. можно увеличить продолжительность работ на этом пути на величину полного резерва, не изменяя продолжительности критического пути.
Но этот резерв нельзя отнести на любую работу, т.к. каждая работа может принадлежать нескольким путям.
Для определения полного резерва, кот можно отнести на данную работу, необходимо рассчитать резервы всех путей, к которым относится данная работа и взять наименьшую величину резерва.
Но это слишком трудоемкий процесс, поэтому используется следующая формула.
Полный резерв показывает, что данную работу можно либо начать позже, либо увеличить продолжительность этой работы на величину резерва.
Использование полного резерва на любую из работ приводят к тому, то эта и все остальные работы данного пути становятся критическими. В результате работе, которая стоит в графике дальше от исходного, может не хватить резервов.
Частный резерв показывает, насколько можно увеличить продолжительность данной работы, либо сдвинуть ее раннее начало, не изменяя как РН последних работ, так и конечного срока графика.
Величина частного резерва не превышает величину полного, а сумма частных резервов всегда равноа полному резерву данного пути.
34. Табличный метод расчета аналитических параметров сетевой модели.
Сетевая модель – ориентированный граф изображающий все необходимое, для достиж целей операции в технологич-ой взаимосвязи.
Основные элементы сет модели:
2. Событие- результат выполнения 1 или неск-ких работ, позволяющий начинать след работу, изображ-ся в виде круга.
3. Путь- непрерывная послед-ть работ от исходного до завершающего события сетевой модели.
1)Для всех работ, выходящих из данного события из данного события раннее начало всегда равно 0.
2) Для определения ранних начал последующих работ необходимо определит ранне окончание предыдщуих.
3) Все работы которые выходят из одного и того же события имеют одно и то же раннее начало.
Определение поздних начал и окончанией производится в обратном порядке.
Позднее окончание работ входящих в одно событие равно.
Определение работ составляющих критический путь.
Критические работы – это работы, лежащие на критическом пути и не имеющие резервов времени.
Некритические работы – это работы не лежащие на критическом пути.
Полный резерв показывает, что данную работу можно либо начать позже, либо увеличить продолжительность этой работы на величину резерва.
Использование полного резерва на любую из работ приводят к тому, то эта и все остальные работы данного пути становятся критическими. В результате работе, которая стоит в графике дальше от исходного, может не хватить резервов.
Частный резерв показывает, насколько можно увеличить продолжительность данной работы, либо сдвинуть ее раннее начало, не изменяя как РН последних работ, так и конечного срока графика.
Величина частного резерва не превышает величину полного, а сумма частных резервов всегда равно полному резерву данного пути.
2. Резервы времени выполнения работ сетевого графика
Резервы времени построенного сетевого графика оценивают только для некритических работ, так как для работ, лежащих на критическом пути все резервы равны нулю.
Можно рассчитать четыре вида резервов времени выполнения работы :
;
;
;
Полный резерв – это максимальное время, на которое можно перенести начало работы или увеличить продолжительность работы без изменения общего срока выполнения комплекса работ.
Полный резерв времени определяется как резерв времени максимального пути, проходящего через эту работу.
Если полный резерв времени работы использовать именно для этой работы, то все остальные работы максимального пути, проходящего через эту работу, резервов времени иметь не будут.
Гарантийный резерв есть часть полного резерва времени этой работы за вычетом резерва времени работ, предшествующих событию.
Свободный резерв представляет собой максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы при условии, что все события сети наступают в свои ранние сроки. Этот резерв – часть полного резерва.
Использование резерва одной работы может уменьшать резервы последующих или предыдущих работ. Иногда продолжительность времени выполнения работы может быть увеличена без изменения резервов времени предшествующих и последующих работ. Такое возможное увеличение времени работы называется независимым резервом времени (если НР получается отрицательным, то его нужно считать нулевым).
В отличие от полного резерва времени, который в случае его использования отнимает резервы времени работ, лежащих на предшествующем и последующем отрезках максимального пути, проходящего через эту работу, независимый резерв времени работы принадлежит только для данной работы. Его нельзя передать ни предшествующим, ни последующим работам, находящимся на ее максимальном пути, проходящим через эту работу.
Использование независимого резерва времени на работе, которая его имеет, не влияет на ранние и поздние сроки свершения всех событий и работ сети.
Независимый резерв времени работы представляет собой остаток от ее полного резерва времени, если за счет последнего полностью сохранены резервы времени начального и конечного событий данной работы. Таким образом, величина независимого резерва времени работы показывает продолжительность вынужденного ожидания наступления конечного события данной работы, что позволяет снять с этой работы часть ресурсов, чтобы перебросить их на более напряженные работы.
На критическом пути резервов времени для выполнения работы нет. Следовательно, задержка в выполнении какой-либо одной работы приведет к задержке выполнения всего комплекса работ. Следовательно, руководителю необходимо следить за выполнением работ, составляющих критический путь, в первую очередь, выделяя для него ресурсы – трудовые и материальные. Работы, лежащие не на критическом пути, имеют достаточный резерв времени, значит, их выполнение можно отнести на период менее загруженный, и контролировать их выполнение выборочно или возложить на подчиненных руководство ими.
Сетевой график может быть оптимизирован, т.е. разработан новый план, в соответствии с которым комплекс работ может быть выполнен с меньшей затратой материальных средств или в более короткие сроки.
Параметры сетевых моделей и методы их расчета
Сетевая модель имеет ряд характеристик, которые позволяют определить степень напряженности выполнения отдельных работ, а также всего их комплекса и принять решение о перераспределении ресурсов.
Ранний срок наступления события tр(i) — самый ранний из возможных сроков наступления события. Он равен продолжительности максимального пути от исходного события до данного.
tр(i) = max t[Lр(i)] (2.1)
Например, tр(7)=19, т.к. L1=(1,2,4,7), L2=(1,3,4,7),
t(L1)=5+12=17 < t(L2)=7+12=19.
Ранний срок начала работы tр.н.(i,j) равен продолжительности максимального пути от исходного до начального события данной работы.
tр.н.(i,j)=max t[Ln(i)](2.2)
Например, tр.н.(7,11)=19, т.к. L1=(1,2,4,7), L2=(1,3,4,7),
t(L1)=5+12=17
Ранний срок начала работы равен раннему сроку наступления начального события данной работы.
tр.н.(i,j) = tр(i) (2.3)
Ранний срок окончания работы tр.о.( i,j) равен сумме раннего срока начала работы и продолжительности данной работы.
tр.о.(i,j)= tр.н.(i,j) + t(i,j) (2.4)
Например, tр.о.(7,11)= tр.н.(7,11) + t(7,11)= 19+8=27.
Поздний срок наступления события tп( i) равен разности между продолжительностью критического пути и продолжительностью максимального пути от данного события до завершающего.
tп(i) =Tкр — max t[Lк(i)](2.5)
Например, tп(7)=19, т.к. L1=(7,11), L2=(7,9,11), t(L1)=8 > t(L2)=4,
tп(7) = Tкр — max t[Lк(7)]=27 — 8=19.
Для событий критического пути tр( i)=tп(i), для других событий tр(i)tп(i).
Поздний срок окончания работы tп.о.( i,j) – это самый поздний срок окончания работы, при котором планируемый срок окончания проекта не меняется, он равен разности между продолжительностью критического пути и продолжительностью максимального пути от конечного события данной работы до завершающего события.
tп.о.(i,j)=Tкр — max t[Lк(j)] (2.6)
Поздний срок окончания работы равен позднему сроку наступления конечного события tп.о.(i,j) = tп(j). Например, tп.о.(4,7) = tп(7)=19.
Поздний срок начала работы tп.н.( i,j) – самый поздний срок начала работы, при котором планируемый срок окончания проекта не меняется.
tп.н.(i,j)= tп .о.(i,j) — t(i,j) (2.7)
Например, tп.н.(4,7)= tп.о.(4,7) — t(4,7)=19-12=7.
Для работ критического пути ранние и поздние сроки начала и окончания работ равны: tр.н.(4,7)= tп.н.(4,7)=7, tр.о.(4,7)= tп.о.(4,7)=19.
Работы, не лежащие на критическом пути, могут иметь резервы времени.
Полный резерв времени Rп( i,j) – максимальное время, на которое можно увеличить продолжительность данной работы, не изменяя продолжительности критического пути.
Rп (i,j)= tп(j) — tр(i) — t(i,j)
Rп(i,j)= tп.н (i,j) — tр.н.(i,j) (2.8)
Rп (i,j)= tп.о.(i,j) — tр.о.(i,j)
Свободный резерв времени Rс( i,j) равен разности между ранним началом последующей работы и ранним окончанием рассматриваемой работы.
Rс(i,j)= tр.н (j,к) — tр.о.(i,j) (2.9) Перейти к онлайн решению своей задачи