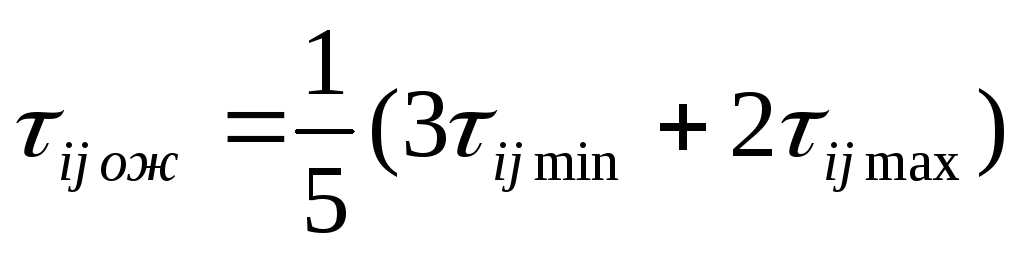Методы расчета временных параметров и критического пути сетевой модели проекта
Если размеры сетевого графика невелики, то его временные параметры и критический путь могут быть найдены путем непосредственного рассмотрения графика вершина за вершиной, работа за работой. Но, естественно, по мере увеличения масштабов модели вероятность появления ошибки в расчетах будет возрастать в геометрической прогрессии. Поэтому, даже при небольших размерах модели целесообразно воспользоваться одним из наиболее подходящих алгоритмических методов расчета, позволяющих подойти к этой задаче формально.
Самыми распространенными методами расчета временных параметров сетевой модели являются табличный и матричный. Поэтому, даже если исходная информация по сетевой модели представлена в виде сетевого графика или временной диаграммы, приступая к анализу, ее следует привести к табличной либо матричной форме.
В качестве примера будем рассматривать модель, заданную изначально сетевым графиком, приведенным на рис. 6.
Рисунок 6. Пример сетевого графика для иллюстрации методов расчета временных параметров
Как табличный, так и матричный метод расчета временных параметров сетевой модели основывается на следующих соотношениях, вытекающих из определений временных параметров. Для удобства понимания индекс работы, как правило, состоит из двух букв, например, [ij], первая из которых соответствует индексу начального события работы, а вторая – индексу конечного события работы. С учетом этого замечания:
- Раннее время начала работы [ij] совпадает с ранним временем наступления события [i], т.е. ESTij = EET [i].
- Позднее время окончания работы [ij] совпадает с поздним временем наступления события [j], т.е. LFTij = LET [j].
- Раннее время окончания работы [ij]:
- Позднее время начала работы [ij]: LSTij = LFTij – tij.
- Раннее время наступления события [j] совпадает с самым поздним (максимальным) ранним временем окончания из всех тех работ, для которых данное событие является конечным, т.е. EET[j] = max , где [rj], [nj], . [mj] – индексы работ, для которых событие [j] является конечным.
- Позднее время наступления события [j] совпадает с самым ранним (минимальным) поздним временем начала из всех тех работ, для которых данное событие является начальным, т.е. LET[j] = min < LSTjr, LSTjn, . LSTjm>, где [jr], [jn], . [jm] – индексы работ, для которых событие [j] является начальным.
- Для исходного и заключительного события сетевой модели справедливо: EET[s] = LET[s]
- Но если для исходного события принимается, как правило, момент времени, равный 0, то для заключительного события он появляется в результате расчетов и по нему можно судить о продолжительности критического пути. Итак, для заключительного события справедливо: EET[f] = LET[f] = TK, где TK – продолжительность критического пути.
- Полный резерв времени выполнения работы [ij]: TFij = LЕT[j] – EET[i] – tij.
- Свободный резерв времени выполнения работы [ij]: FFij = EЕT[j] – EET[i] – tij.
- Независимый резерв времени выполнения работы [i]: IFi = EЕT[j] – LET[i] – tij.
Расчет и исследование сетевой модели
Расчет сетевой модели заключается в определении
- критического времени и критического пути;
- полных, независимых и частных резервов времени работ;
- резервов времени событий.
Удобно исследование сетевой модели изображать линейной диаграммой (графиком Ганта), в которой каждая работа – отрезок, параллельный оси времени. Длина этого отрезка равна продолжительности работы в выбранном масштабе. События i и j начала и конца работы uij ставят в начале и конце соответствующего отрезка. Отрезки располагают один над другим, снизу вверх, в порядке возрастания индексации. Момент наступления исходного события равен 0. Каждый отрезок (i,j) размещают на диаграмме таким образом, чтобы его начало совпало с самым правым концом всех отрезков, входящих в событие i. На рис. 2.11 представлена линейная диаграмма сетевого графика, изображенного на рис. 2.10. 
2
4 5 
Н 
3 5 
3 4 
2 5 
1 3 
0 3 
0 2 1
0 1 
0 1 2 3 4 5 10 t Рис. 2.11 Линейная диаграмма сетевой модели Не трудно заметить, что исходная линейная диаграмма отражает такой ход ведения работ, при котором все работы начинаются в свои ранние сроки. С помощью линейной диаграммы можно определить критический путь, критическое время, резервы времени всех работ и т.д. Критический путь представляет собой цепочку отрезков-работ, соединяющих завершающее событие самого правого отрезка с исходным. Критическое время равно самой правой координате всех отрезков линейной диаграммы. Полный резерв времени работы равен максимальному сдвигу соответствующего отрезка вправо, который при этом не приведет к увеличению критического времени. Так, Pп(4,5) = 6, Pп(1,3) = 6. На диаграмме символами н, 1, 2 обозначены работы, имеющие соответственно независимый и частные резервы 1-го и 2-го вида. Жирной рамкой выделены критические работы. После расчета сетевой модели переходят к ее исследованию, целью которого является получение такого графика выполнения работ, который наиболее полно удовлетворяет каким-то критериям. Для этого можно увеличивать длительность или задерживать начало выполнения работ, во-первых, на величину их независимых резервов, что не требует пересчета резервов других работ, во-вторых, на величину их свободного резерва (т.е. частного резерва 2-го вида), так как это не влечет за собой пересчет резервов последующих работ и т.д. Тем самым от исходной переходят к другим линейным диаграммам, в которых работы могут либо начинаться не в свои ранние сроки, либо выполняться более начальной продолжительности, однако при этом срок завершения всего комплекса работ не меняется, оставаясь равным критическому.
Лекция 2.3.3. Более сложные сетевые модели
Вероятностная временная сетевая модель
Второй также наиболее часто встречающейся сетевой моделью является одноцелевая временная вероятностная модель. Эта модель отличается тем, что продолжительности работ задаются как случайные величины. Такая модель более близка к условиям подсистемы ТПП. В настоящее время существуют две методики задания параметров распределения продолжительности работ:
- трехоценочная;
- двухоценочная.
При использовании первой методики эксперт задает 3 оценки продолжительности работы:
- оптимистическую τijmin;
- наиболее вероятную τijнв;
- пессимистическую τijmax.
Наиболее вероятная оценка – это время, необходимое для выполнения данной работы при нормальных, чаще всего встречающихся условиях (определяется первой). Оптимистическая оценка – это время, необходимое для выполнения работы при наиболее благоприятном стечении обстоятельств (определяется второй). Пессимистическая оценка – это время, необходимое для выполнения работ при неблагоприятных условиях. Как вы знаете, продолжительность работы связана с количеством ресурсов, выделяемых на ее проведение. Поэтому необходимо отметить, что для определения временных характеристик продолжительности работы эксперты должны руководствоваться максимальными значениями ресурсов. При использовании второй методики исключается наиболее вероятная оценка τijнв, определение которой вызывает у экспертов особые трудности и пользуются только двумя оценками τijmin и τijmax. На основе опытных данных установлено, что в большинстве случаев законы распределения продолжительностей работ обладают положительной асимметрией, распределение более круто в области τijmin. Это позволило из множества теоретических законов распределения выбрать закон β-распределения, кривая плотности которого имеет вид, представленный на рис.2.12. П
ри этом оценки математического ожидания и дисперсии β-распределения определяются следующим образом: 
P
(t) 
мода tijож tij
tijmin tijнв tijmax Рис. 2.12 Вид плотности распределения продолжительности работ По второй методике: П
ервый этап расчета временной вероятности модели заключается в определении:
- ожидаемого времени выполнения работ τijож и оценки дисперсии σ 2 ij.
- всех временных параметров модели по тем же алгоритмам, что и у детерминированной временной модели, заменив τij на τijож.
Второй этап расчета заключается в определении вероятности наступления каждого события сети не позднее директивных сроков. Обозначим через μi – случайную величину, характеризующую ранний срок наступления события i. Если событие i связано с исходным событием лишь одним путем L(0i), то оценка математического ожидания μiопределяется суммой ожидаемых продолжительностей работ, принадлежащих этому пути tож[L(0i)], а оценка дисперсии σ 2 (μi) представляет собой сумму дисперсий продолжительностей тех же работ. В случае, если имеется более одного пути, предшествующего i-му событию, то упрощенно предполагается, что в этом случае μi и σ 2 (μi) вычисляется с использованием характеристик предшествующего пути, имеющего максимальную продолжительность max t[L(0i)]. Если же несколько путей имеют максимальную продолжительность, то для определения дисперсии выбирается путь с максимальной дисперсией продолжительности, так как он характеризуется большой неопределенностью, а, следовательно, дает более надежный результат. Т
аким образом, где k означает работы, принадлежащие самому длинному пути, предшествующему событию i. При этом предполагается, что величина μi является суммой независимых случайных величин, и, следовательно, согласно центральной предельной теореме, распределение μi близко к нормальному, а величины (*) являются оценками математического ожидания и дисперсии. Поскольку μi есть ранний срок наступления события i, то это событие наступит не позднее директивного срока TДi с вероятностью P( μi ≤ TДi ). Переходя к стандартному нормальному распределению величины п
олучим З
десь Ф – стандартное (нормированное) нормальное распределение величиныxi, Ki – квантиль данного распределения. Обычно в качестве директивных сроков всех событий кроме завершающего используют поздний срок его свершения Ti п . Для завершающего события величина TД определяется лицом, принимающим решение, причем Tn P ож = tкр.
4,Основные временные параметры сетевых моделей
Расчет сетевой модели заключается в определении следующих временных расчетных параметров отдельных составляющих ее работ: 1. Ткр — продолжительность критического пути – максимальная продол-жительность выполнения всех работ, что в конечном итоге определяет сроки строительства; 2. Ri-j – общий (полный) резерв времени работы i-j – максимальное время, на ко-торое можно увеличить продолжительность выполнения работы i-j, или перенести сроки ее начала на более позднее не изменяя при этом продолжительность критического пути; 
3. ri-j – частный (свободный) резерв времени – максимальное время, на которое можно увеличить продолжительность выполнения работы i-j, или перенести сроки ее начала на более позднее не изменяя при этом ранних начал последующих работ; 
4. ti-j – продолжит-ть выполнения работы i-j; 5. ti-jрн – время раннего начала работы i-j – самый ранний срок возможного начала работы i-j; 6. ti-jро – время раннего окончания работы i-j – самый ранний срок воз-можного окончание работы i-j; 7. ti-jпн – время позднего начала работы i-j – самый поздний срок возмож-ного начала работы i-j; 8. ti-jпо – время позднего окончания работы i-j – самый поздний срок окон-чания работы i-j; Существуют различные методы расчета временных параметров сетевых моделей: -графический (секторный, или на самом графике) -аналитический -табличный -метод потенциалов -метод дроби Расчет можно выполнять как вручную, так и помощью ЭВМ.
5. Исходные данные по разработке пос.
- Технико-экономическое обоснование или технико-экономические расчеты, обосновывающие хозяйственную их необходимость и экономическую целесообразность строительства данного объекта и задания на его проектирование.
- Материалы инженерных изысканий.
- Плановые документы, устанавливающие сроки строительства.
- Согласованные генподрядными и субподрядными организациями решения по применению материалов, конструкций, средств механизации, порядка обеспечения мест строительства водой, врем. инженерными сетями.
- Сведения обусл. поставки и транспортирования с предприятий-поставщиков строительных конструкций, материалов и оборудования.
- Специальные требования к строительству сложных и уникальных сооружений.
- Сведения об усл. произв-ва СМР на реконструируемых объектах.
- Объемно-планировочные и конструктивные решения зданий и сооружений и основные технологические схемы производства основных комплексов СМР.
- Сведения об условиях обеспечения строительства кадрами.
- Сведения об условиях обеспечения транспортом.
- Сведения о дислокации, мощностях и специализации генподрядных организаций данного территориального региона и возможности их перебазирования.
- Сведения об условиях обеспечения строительства жилыми и культурно-бытовыми зданиями.
- Сведения о наличии производственной базы стройиндустрии, номенклатуры выпускаемой ими продукции возможности максимального ее использования.
- Сведения об условиях строительства, предусмотренные контрактами с иностранными фирмами.
Для продолжения скачивания необходимо пройти капчу: