Временные параметры сетевых графиков
В (табл. 1) приведены основные временные параметры сетевых графиков.
Таблица 1 – Временные параметры сетевых графиков
Элемент сети, характеризуемый параметром
Условное обозначение параметра
Ранний срок свершения события
Поздний срок свершения события
tР (i)
tП (i)
Ранний срок начала работы
Ранний срок окончания работы
Поздний срок начала работы
Поздний срок окончания работы
Полный резерв времени работы
Свободный резерв времени работы
tРН (i, j)
tРО (i, j)
tПН (i, j)
tПО (i, j)
RП (i, j)
RС (i, j)
Продолжительность критического пути
t (L)
Событие не может наступить прежде, чем свершатся все предшествующие работы. Поэтому ранний срок tР (i) свершения i – того события определяется продолжительностью максимального пути, предшествующего этому событию: tР (i)=max t(LПi), где LПi – любой путь, предшествующий i – тому событию, то есть путь от исходного до i –того события сети.
Ранний срок свершения события i – это самый ранний срок, к которому завершаются все работы, предшествующие этому событию.
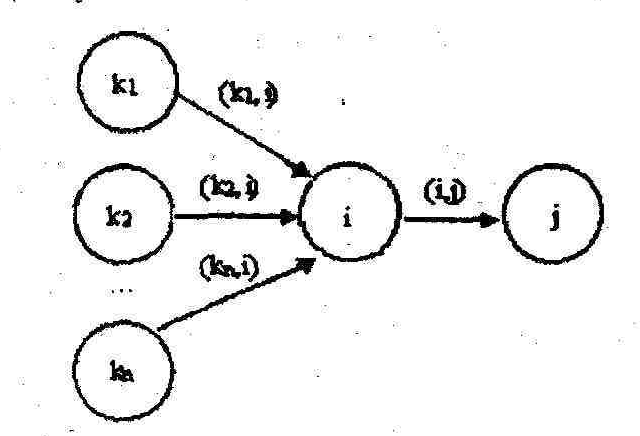
Если событие i имеет несколько предшествующих работ (рис.5), то ранний срок свершения события i находится так:
Пусть B(i) – множество работ, непосредственно предшествующих событию i. Тогда
tР (i)=max< tР (k)+ t (k,i)>,(k,i) B(i) (1)
Задержка свершения события i по отношению к своему раннему сроку не отразится на сроке свершения завершающего события (значит, и на сроке выполнения комплекса работ) до тех пор, пока сумма срока свершения этого события и длины максимального из последующих за ним путей не превысит длины критического пути.
Поэтому поздний срок tП (i) свершения i – того события равен:
tП (i)=tКР – max t(Lci), где Lci – любой путь, следующий за i –м событием, то есть путь от i –того до завершающего события сети.
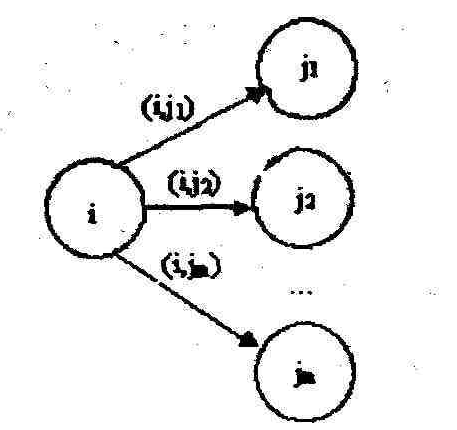
Если событие i имеет несколько последующих работ (рис. 6), то поздний срок свершения события i удобно находить по формуле:
tП (i)= min< tП (j)- t (j,i)>,(j,i) C(i) (2)
где: C(i) – множество работ (j,i), выходящих из вершины i.
При любом поздний срок свершения события i находится так: сначала при i=n полагают tП (i)=tР(n) =tКР, затем последовательно для i равным n-1, n-2,….1 вычисляют по формуле (2).
Резерв времени i – того события определяется как резерв между поздним и ранним сроком его свершения:
Ri = tП(i) – tР(i) (3)
Резерв времени i – того события показывает, на какой допустимый срок можно задержать наступление этого события, не вызывая при этом увеличения времени выполнения комплекса работ.
Критические события резервов времени не имеют, так как любая задержка в свершении события, лежащего на критическом пути, вызовет такую же задержку в свершении завершающего события.
Из этого следует, что для определения критического пути (если он единственный) вовсе не обязательно перебирать все полные пути сетевого графика и определять их длины. Определив ранний срок наступления завершающего события сети, определяют длину критического пути, а выявив события с нулевыми резервами времени, определяют его конфигурацию.
Если критических путей несколько, то выявление их с помощью критических событий может быть затруднительно, так как через часть критических событий могут проходить как критические, так и некритические пути. В этом случае для определения критических путей следует использовать критические работы.
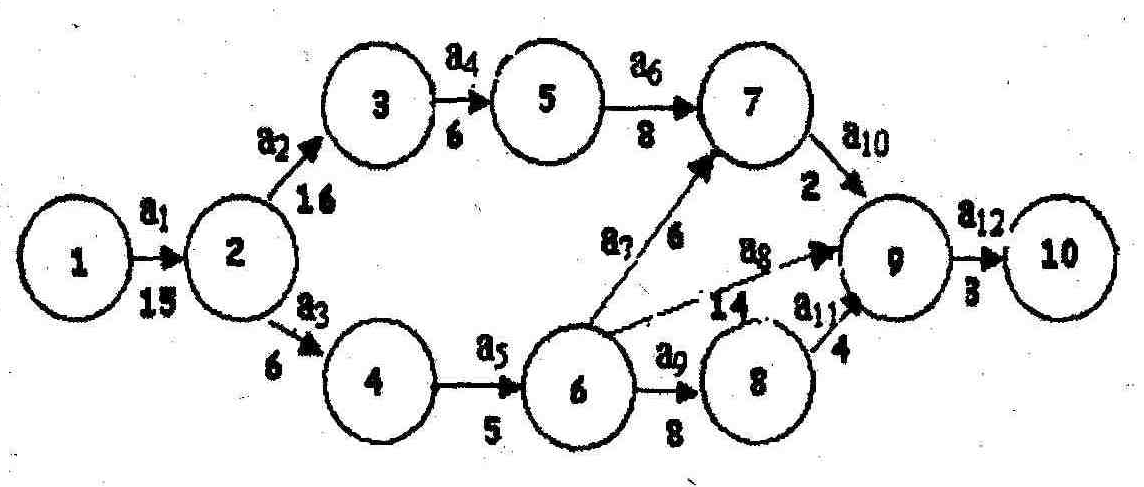
По (рис. 7) рассчитать ранние и поздние сроки свершения событий, а также их резервы. Найти критический путь выполнения комплекса работ и его длину.
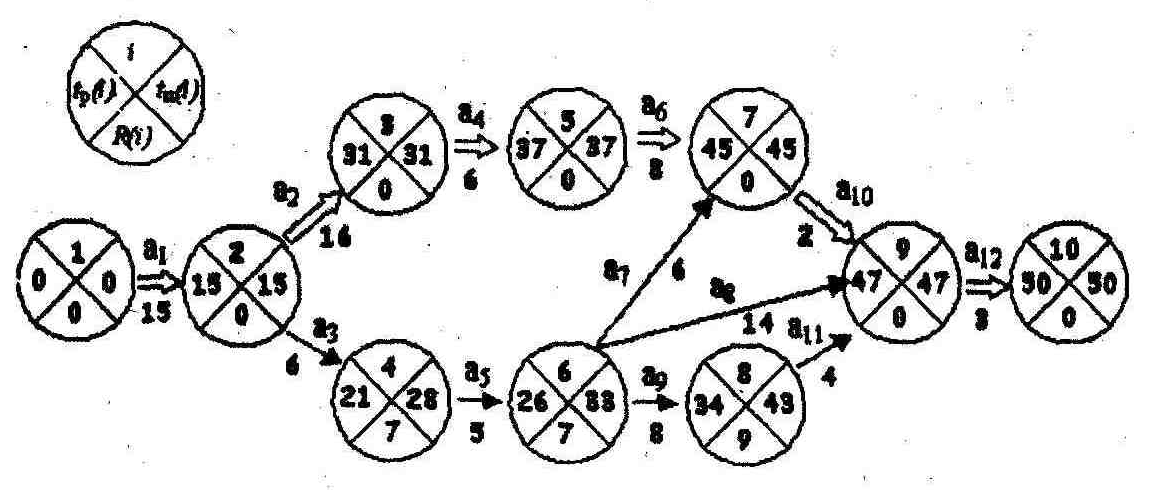
Каждую вершину сети разбиваем на четыре сектора. В верхней части сектора отмечается номер события i, в левой – ранний срок свершения события i, в правой – поздний срок свершения события i, в нижней – резерв времени этого события (рис. 8).
Сначала по формуле (1) находим ранние сроки свершения события i и заносим их в левые секторы сетевого графика. Имеется:
Теперь рассчитываются поздние сроки свершения событий. Расчет начинается с последнего события и затем, «пятясь», двигается к первому событию.
Для i=10 поздний срок свершения события tП (10)= tР (10)=47+3=50. Далее по формуле (2) имеется:
Результаты расчета заносят в правые секторы вершин сети.
По формуле (3) рассчитывают резервы времени каждого события и заносят их в нижние секторы вершин.
R(1) =0-0=0;
R(2) =15-15=0;
Чтобы рассчитать критический путь фиксируются события, не имеющие резервов времени. Это события 1,2,3,5,7,9,10. Следовательно, путь 1→2→3→5→7→9→10 является критическим.
Длина критического пути tКР= tР (10)=50.
Критический путь отмечается на сетевом графике двойной стрелкой.
Расчет сроков свершения событий
Важнейшим показателем сетевого графика являются резервы времени. Резервы времени каждого пути показывают, на сколько может быть увеличена продолжительность данного пути без ущерба для наступления завершающего события. Поскольку каждый некритический путь сетевого графика имеет свой полный резерв времени, то и каждое событие этого пути имеет свой резерв времени.
| Элемент сети | Наименование параметра | Условное обозначение параметра |
| Событие i | Ранний срок свершения события | tp(i) |
| Поздний срок свершения события | t(i) | |
| Резерв времени события | R(i) | |
| Работа (i, j) | Продолжительность работы | t(i,j) |
| Ранний срок начала работы | t рн (i,j) | |
| Ранний срок окончания работы | t po (i,j) | |
| Поздний срок начала работы | t пн (i,j) | |
| Поздний срок окончания работы | t по (i,j) | |
| Полный резерв времени работы | R п (i,j) | |
| Путь L | Продолжительность пути | t(L) |
| Продолжительность критического пути | tkp | |
| Резерв времени пути | R(L) |
Решение. Все вычисления будем заносить в таблицу.
Резерв времени события показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ.
При определении ранних сроков свершения событий tp(i) двигаемся по сетевому графику слева направо и используем формулы (1), (2).
Расчет сроков свершения событий.
Для i=1 (начального события), очевидно tp()=0.
i=1: t p (1) = t p (0) + t(0,1) = 0 + 5 = 5.
i=2: t p (2) = t p (0) + t(0,2) = 0 + 7 = 7.
i=3: t p (3) = t p (1) + t(1,3) = 5 + 3 = 8.
i=4: t p (4) = t p (2) + t(2,4) = 7 + 6 = 13.
i=5: max(t p (1) + t(1,5);t p (3) + t(3,5);t p (4) + t(4,5)) = max(5 + 5;8 + 8;13 + 4) = 17.
Длина критического пути равна раннему сроку свершения завершающего события 5: tkp=tp(5)=17
При определении поздних сроков свершения событий tп(i) двигаемся по сети в обратном направлении, то есть справа налево и используем формулы (3), (4).
Для i=5 (завершающего события) поздний срок свершения события должен равняться его раннему сроку (иначе изменится длина критического пути): t п (8)= t р (8)=17
Максимальное значение: 17. Записываем его в графу 7 по всем строчкам, оканчивающимся на номер последнего события 5.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 4. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 4.
i=4: t п (4) = t п (5) — t(4,5) = 17 — 4 = 13.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 3. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 3.
i=3: t п (3) = t п (5) — t(3,5) = 17 — 8 = 9.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 2. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 2.
i=2: t п (2) = t п (4) — t(2,4) = 13 — 6 = 7.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 1. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 1.
i=1: min(t п (3) — t(1,3);t п (5) — t(1,5)) = min(9 — 3;17 — 5) = 6.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 0. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 0.
i=0: min(t п (1) — t(0,1);t п (2) — t(0,2)) = min(6 — 5;7 — 7) = 0.
| Номер события | Сроки свершения события: ранний tp(i) | Сроки свершения события: поздний tп(i) | Резерв времени, R(i) |
Перечень работ и их продолжительность перенесем во вторую и третью графы. При этом работы следует записывать в графу 2 последовательно: сначала начиная с номера 0, затем с номера 1 и т.д.
Во второй графе поставим число, характеризующее количество непосредственно предшествующих работ (КПР) тому событию, с которого начинается рассматриваемая работа.
Так, для работы (0,1) в графу 1 поставим число 0, т.к. на номер 0 оканчиваются 0 работы:.
Далее заполняем графы 4 и 5. Для работ, имеющих цифру 0 в графе 2, в графу 4 также заносятся нули, а их значения в графе 5 получаются в результате суммирования граф 3 и 4.
Для заполнения следующих строк графы 4, т.е. строк начиная с номера 2, просматриваются заполненные строки графы 5, содержащие работы, которые оканчиваются на этот номер, и максимальное значение переносится в графу 4 обрабатываемых строк.
Этот процесс повторяется до тех пор, пока не будет заполнена последняя строка таблицы.
Графы 6 и 7 заполняются обратным ходом, т.е. снизу вверх. Для этого просматриваются строки, оканчивающиеся на номер последнего события, и из графы 5 выбирается максимальная величина, которая записывается в графу 7 по всем строчкам, оканчивающимся на номер последнего события (т.к. tр(i)= tп(i)).
Процесс повторяется до тех пор, пока не будут заполнены все строчки по графам 6 и 7.
Содержимое графы 8 равно разности граф 6 и 4 или граф 7 и 5.
Анализ сетевой модели по времени
| Работа (i,j) | Количество предшествующих работ | Продолжительность tij | Ранние сроки: начало tij Р.Н. | Ранние сроки: окончание tij Р.О. | Поздние сроки: начало tij П.Н. | Поздние сроки: окончание tij П.О. | Резервы времени: полный tij П | Резервы времени: свободный tij С.В. | Резервы времени: событий Rj |
| (0,1) | |||||||||
| (0,2) | |||||||||
| (1,3) | |||||||||
| (1,5) | |||||||||
| (2,4) | |||||||||
| (3,5) | |||||||||
| (4,5) |
а) графы 1 и 3 заполняются на основе исходных данных.
б) в графе 2 записывается количество предшествующих работ по сетевому графику или определяется из графы 1 по числу работ, имеющих второй цифрой в коде ту, с которой начинается данная работа.
г) в графе 4 раннее начало работ, выходящих из исходного события, а раннее окончание этих работ равно их продолжительности (гр. 5). Раннее начало последующих работ определяется путем выбора максимального из сроков раннего окончания предшествующих работ. Количество сравниваемых сроков равно количеству предшествующих работ графы 2. Раннее начало последующих работ можно определить после того, как найдено раннее окончание предшествующих. В свою очередь раннее окончание каждой работы находится как сумма величин раннего начала и продолжительности данной работы;
г) продолжительность критического пути определяется после заполнения граф 4 и 5 как максимальная величина из сроков раннего окончания работ, которые ведут к завершающему событию 9;
д) найденная величина критического пути ТKP дням заносится в графу 7 для всех работ, ведущих к завершающему событию. Затем заполнение ведется снизу вверх. Находятся все работы, следующие за рассматриваемой, и определяются разности между поздним окончанием этих работ и их продолжительностями. Минимальная из величин заносится в графу 7;
е) в графе 6 позднее начало работы определяется как разность позднего окончания этих работ и их продолжительности (из значений графы 7 вычитаются данные графы 3);
ж) в графе 8 полный резерв времени работы определяется разностью между значениями граф 7 и 5. Если он равен нулю, то работа является критической;
з) в графе 10 резерв времени событий j определяется как разность позднего окончания работы, заканчивающегося событием j графы 7, и ранним началом работы, начинающимся событием j;
и) значение свободного резерва времени работы определяется как разность значений графы 10 и данных графы 8 и указывает на расположение резервов, необходимых для оптимизации.
Критический путь: (0,2)(2,4)(4,5)