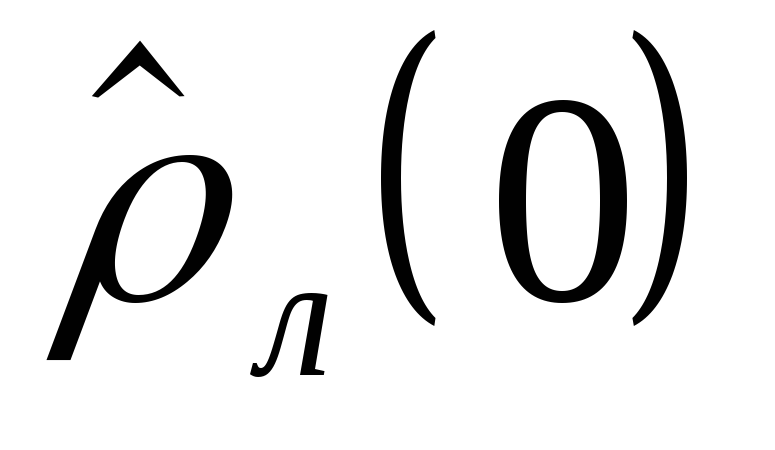Оптимизация сетевой модели может быть

18. Оптимизация сетевых моделей.

После расчета сетевого графика любым из указанных способов его анализируют с целью установления соответствия полученных сроков продолжительности строительства нормативным или директивным срокам. Корректировку сетевого графика называют оптимизацией графика.

Корректировка графика по продолжительности преследует цель сократить критический путь. Сокращения продолжительности критического пути в результате использования резервов времени, выявленных на некритических работах благодаря привлечению дополнительных ресурсов.

Оптимизация сетевого графика может осуществляться по следующим критериям:

· минимизация времени выполнения комплекса работ при заданных затратах на это выполнение;

· минимизация затрат на выполнение комплекса работ при заданном

Целью оптимизации является сокращение времени выполнения проекта в целом. Эта оптимизация имеет смысл только в том случае, когда длительность выполнения работ может быть уменьшена за счет дополнительных ресурсов, что влечет к повышению затрат на выполнение работ. Для оценки величины дополнительных затрат, связанных с ускорением выполнения той или иной работы, используются либо нормативы, либо данные о выполнении аналогичных работ в прошлом.

Исходными данными для проведения оптимизации являются:

· нормальная длительность работы;

· затраты на выполнение работы в нормальный срок;

· затраты на выполнение работы в ускоренный срок.

Оптимизацию можно проводить двумя способами.

Первый способ заключается в уменьшении продолжительности выполнения работ, осуществляемых в нормальном режиме, начиная с тех, которые дают наименьший прирост затрат.

Второй способ заключается в увеличении продолжительности выполнения работ, осуществляемых в ускоренном режиме, начиная с тех, которые дают наибольший прирост затрат.

19. Метод вероятностного моделирования.

Прогнозирование с использованием вероятностных моделей базируются на методе экспоненциального сглаживания. Вероятностные модели по своей сути отличны от экстраполяционных моделей временных рядов, в которых основой является описанные изменения во времени, процесса.

Во временных рядах модели представляют собой некоторую функцию времени с коэффициентами, значения которых оцениваются по наблюдениям. В вероятностных моделях оцениваются вероятности, а не коэффициенты.

Пусть мы имеем n взаимно независимых и исключающих событий. В каждом случае наблюдения измеряются в единой шкале, помещаются в (n+1) ограниченный класс и обозначаются так: . Событие связанное с наблюдением Х (t), соответствует числу интервалов в которое это событие попадает, т.е. существует единственное значение К, такое, что Х. И поэтому К-е событие связывается с наблюдением X(t).

Рассмотрим метод оценивания вероятностей , связанных с различными событиями Х

На первом этапе задаются начальные значения различных вероятностей: :

К = 1,2. n. Наблюдение Х(t) связано с К-м событием следующим образом: если Х то строится единый вектор компонент который равен 0 и К-й компонент равен 1. Это может быть К-м столбцом единичной матрицы ранга К.

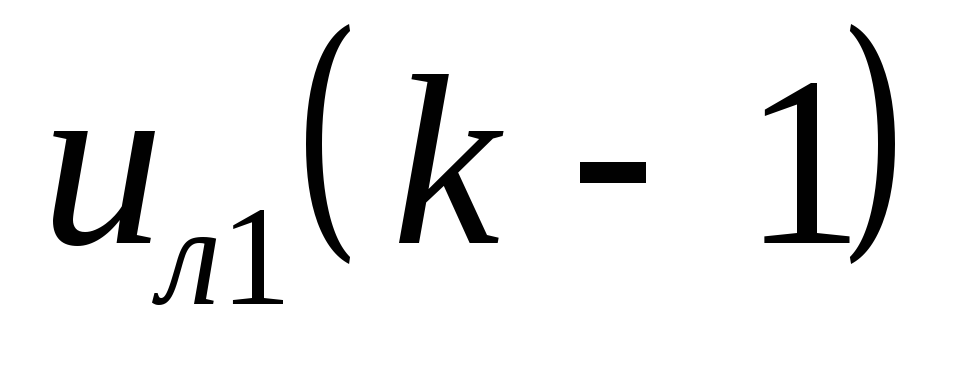
Предположим, что имеются пять классов и наблюдение попало во второй класс, соответствующий единичный вектор будет

Процесс реализующий оценки вероятностей, описывается вектором сглаживания по формуле:

Каждая компонента вектора меняется по закону экспоненциального сглаживания между 0 и 1. Если вероятностный, то все его компоненты должны быть неотрицательными и их сумма должна быть равна 1. Значение оценки есть результат экспоненциального сглаживания, и если распределение вероятностей наблюдений X (t) не меняется, то полученные вероятности и будут действительными вероятностями К-го события.

Значения компонент вектора представляют собой выборку с биноминальным распределением, поэтому дисперсия К-й компоненты будет . Дисперсия оценок К-й вероятности определяется соотношением 

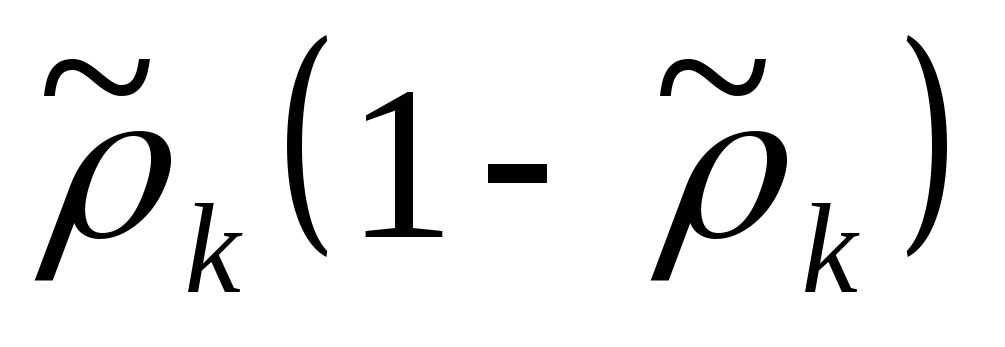
где  — константа сглаживания (01) используемая для получения оценок вектора вероятностей.

Возможны два варианта: в первом варианте пределы классов заданы так, что может быть или очень большим (около 1) или очень маленьким (около 0). Тогда дисперсия компонент вектора вероятностей будет небольшой. Если форма распределения меняется со временем, большое значение компонента сглаживания может быть использована, чтобы устранить влияние “старой” информации.

Во втором варианте распределение вероятностей постоянно во времени и нет необходимости “взвешивать” старую информацию. Малое значение компоненты сглаживания, может использовать меньшие интервалы классов с не очень большими вероятностями. Вероятностная модель оперирует последовательностью наблюдений с учетом их распределения и игнорирует последовательность этой информации уже непосредственно во времени. Поэтому вектор вероятностей , который служит текущей оценкой вероятностей n отдельных событий, является оценкой этих вероятностей в будущем. Последовательность наблюдений может быть представлена как временной ряд х(t), где x измерен по некоторой шкале есть min и max возможных значений наблюдений.

Пусть x случайная величина с ожиданием m и конечной дисперсией . Тогда сумма n случайных выборок будет нормально распределена со средним nm и дисперсией и вероятности как сумма точек наблюдений будут распределены нормально.

Пусть случайная величина Х распределенная между нулем и единицей. Введем функцию f(x) =

если Yn — сумма N случайных выборок, тогда функция распределения этих сумм будет

где 0yN. Находим среднее значение и дисперсию для величины y.

Yp является точкой распределения и ее можно выразить через среднюю и дисперсную распределения

, где Kp — некоторый множитель, учитывающий число степеней свободы распределения.

Данное управление может служить основой оценок для вероятностной модели. При достаточном количестве исходной информации вероятностная модель может дать вполне надежный прогноз. Недостатком является требование достаточно большого количества наблюдений и назначение начального распределения, что может привести к неправильным оценкам.

Экстраполяция базируется на допущениях: 1) развитие явления может быть с достаточным основанием охарактеризовано плановой траекторией-трендом; 2) общие условия, определяющие тенденцию развития в прошлом, не претерпят существенных изменений в будущем. Недостатки данного метода: 1) он исходит из прошлого и настоящего и поэтому накапливаются погрешности; 2) необходимый выбор периода упреждения прогноза. Положительные рез-ты метод дает на 1-2 года, дальше будут ошибки; 3) практическая невозможность получения статистическими методами кривой требуемой формы. Поэтому, чтобы предупредить ошибки в прогнозе, метод экстраполяции следует сочетать с другими методами прогнозирования.

Метод экстраполяции применяется при стабильности системы, устойчивости явлений, когда динамика процессов, показателей в перспективе опред-ся тенденциями их изменения в прошедшем периоде. Предполагается, что развитие идет непрерывно, гладко, силы прошлого в состоянии контролировать будущее. Прогноз становится проекцией прошлого в будущее.

Источник

3.4. Оптимизация сетевой модели

После расчета всех параметров сетевого графика производится его оптимизация. Сетевой график следует проанализировать с целью сокращения критического пути, затрат ресурсов, уменьшения ненужных резервов.

Под оптимизацией сетевой модели следует понимать процесс улучшения первоначального плана по различным показателям: времени, стоимости, количеству исполнителей.

Одним из методов оптимизации является выявление возможного сокращения выполнения работы и определение необходимых для этого затрат. При этом в зависимости от полноты решаемых задач оптимизация может быть частной и комплексной (полной). Видами частной оптимизации являются:

1) минимизация продолжительности выполнения разработки при заданной стоимости;

2) минимизация стоимости при заданной продолжительности.

Комплексная оптимизация — это нахождение такого варианта, при котором соотношения затрат и сроков выполнения в зависимости от конкретных целей были бы наилучшими, т.е. оптимальными. При комплексной (полной) оптимизации допускается повышение затрат при нормальном и экстренном (предельном) режиме работы с целью сокращения сроков или наоборот, увеличения сроков для обеспечения экономии затрат.

Краткая характеристика метода оптимизации

Все работы сетевой модели требуют различных затрат при нормальном и экстренном (предельном) режиме работы. Предельная продолжительность, т.е. минимально возможный срок проведения работы, требует больших затрат на ее проведение, чем при нормальном режиме работы.

Поэтому оптимизация сетевого графика по параметру «время-затраты» и предполагает нахождение такого плана выполнения комплекса работ, который обеспечивал бы достижение поставленной цели в наименьшие сроки и с минимальными затратами.

Оптимизацию следует осуществлять путем направленной корректировки последовательными «шагами» (итерациями). Шаги корректировки заключаются в последовательном сокращении сроков выполнения отдельных работ при минимальном увеличении их стоимости.

Сначала определяют все полные пути сетевой модели и рассчитывают их продолжительность. Определяют из них критический путь, как путь, имеющий наибольшую продолжительность.

Затем переходят к выполнению первой итерации.

Сокращают продолжительность критического пути до величины подкритического (максимального из оставшихся) по самой дешевой работе, уменьшая ее продолжительность. При этом увеличение стоимости будет минимальным. В результате 1-й итерации мы имеем два, одинаковой величины, критических пути, меньшие, чем первоначальный критический путь.

Теперь можно переходить ко 2-й итерации. Сокращаем продолжительность нескольких критических путей, полученных в ходе 1-й итерации, до подкритического по минимальной сумме затрат сокращаемых работ.

Далее процесс повторяется аналогичным образом до тех пор, пока существует возможность дополнительного сокращения продолжительности всех путей за счет уменьшения сроков выполнения наиболее дешевых работ.

Постоянно сравнивая предельные сроки выполнения работ критического пути с полученными в результате последней итерации результатами, останавливаемся тогда, когда убеждаемся, что дальнейшее сокращение всего комплекса работ невозможно.

Таким образом, относительно первоначального варианта продолжительность работ значительно сокращается, а затраты при этом увеличиваются относительно немного, этим достигается цель процесса оптимизации.

Источник