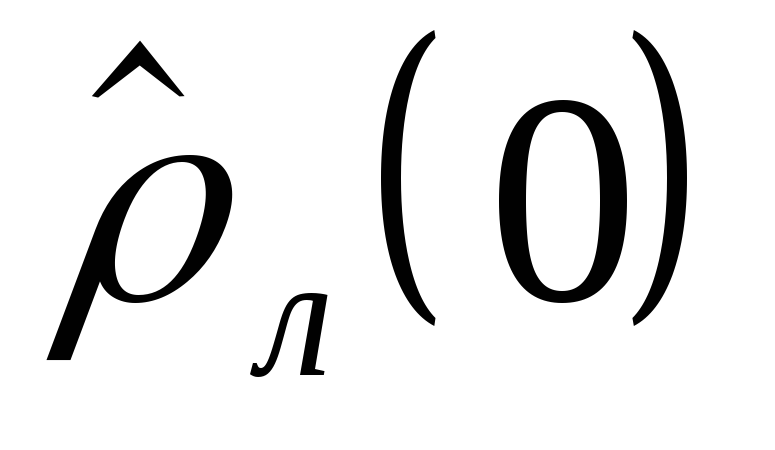Оптимизация сетевой модели может предполагать

18. Оптимизация сетевых моделей.

После расчета сетевого графика любым из указанных способов его анализируют с целью установления соответствия полученных сроков продолжительности строительства нормативным или директивным срокам. Корректировку сетевого графика называют оптимизацией графика.

Корректировка графика по продолжительности преследует цель сократить критический путь. Сокращения продолжительности критического пути в результате использования резервов времени, выявленных на некритических работах благодаря привлечению дополнительных ресурсов.

Оптимизация сетевого графика может осуществляться по следующим критериям:

· минимизация времени выполнения комплекса работ при заданных затратах на это выполнение;

· минимизация затрат на выполнение комплекса работ при заданном

Целью оптимизации является сокращение времени выполнения проекта в целом. Эта оптимизация имеет смысл только в том случае, когда длительность выполнения работ может быть уменьшена за счет дополнительных ресурсов, что влечет к повышению затрат на выполнение работ. Для оценки величины дополнительных затрат, связанных с ускорением выполнения той или иной работы, используются либо нормативы, либо данные о выполнении аналогичных работ в прошлом.

Исходными данными для проведения оптимизации являются:

· нормальная длительность работы;

· затраты на выполнение работы в нормальный срок;

· затраты на выполнение работы в ускоренный срок.

Оптимизацию можно проводить двумя способами.

Первый способ заключается в уменьшении продолжительности выполнения работ, осуществляемых в нормальном режиме, начиная с тех, которые дают наименьший прирост затрат.

Второй способ заключается в увеличении продолжительности выполнения работ, осуществляемых в ускоренном режиме, начиная с тех, которые дают наибольший прирост затрат.

19. Метод вероятностного моделирования.

Прогнозирование с использованием вероятностных моделей базируются на методе экспоненциального сглаживания. Вероятностные модели по своей сути отличны от экстраполяционных моделей временных рядов, в которых основой является описанные изменения во времени, процесса.

Во временных рядах модели представляют собой некоторую функцию времени с коэффициентами, значения которых оцениваются по наблюдениям. В вероятностных моделях оцениваются вероятности, а не коэффициенты.

Пусть мы имеем n взаимно независимых и исключающих событий. В каждом случае наблюдения измеряются в единой шкале, помещаются в (n+1) ограниченный класс и обозначаются так: . Событие связанное с наблюдением Х (t), соответствует числу интервалов в которое это событие попадает, т.е. существует единственное значение К, такое, что Х. И поэтому К-е событие связывается с наблюдением X(t).

Рассмотрим метод оценивания вероятностей , связанных с различными событиями Х

На первом этапе задаются начальные значения различных вероятностей: :

К = 1,2. n. Наблюдение Х(t) связано с К-м событием следующим образом: если Х то строится единый вектор компонент который равен 0 и К-й компонент равен 1. Это может быть К-м столбцом единичной матрицы ранга К.

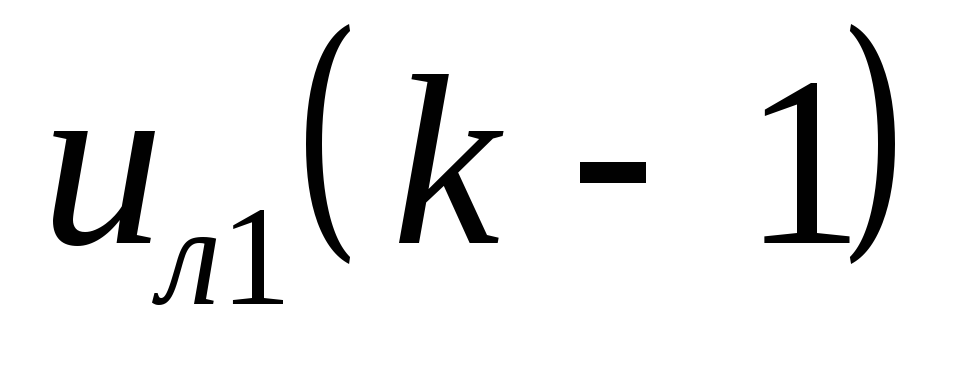
Предположим, что имеются пять классов и наблюдение попало во второй класс, соответствующий единичный вектор будет

Процесс реализующий оценки вероятностей, описывается вектором сглаживания по формуле:

Каждая компонента вектора меняется по закону экспоненциального сглаживания между 0 и 1. Если вероятностный, то все его компоненты должны быть неотрицательными и их сумма должна быть равна 1. Значение оценки есть результат экспоненциального сглаживания, и если распределение вероятностей наблюдений X (t) не меняется, то полученные вероятности и будут действительными вероятностями К-го события.

Значения компонент вектора представляют собой выборку с биноминальным распределением, поэтому дисперсия К-й компоненты будет . Дисперсия оценок К-й вероятности определяется соотношением 

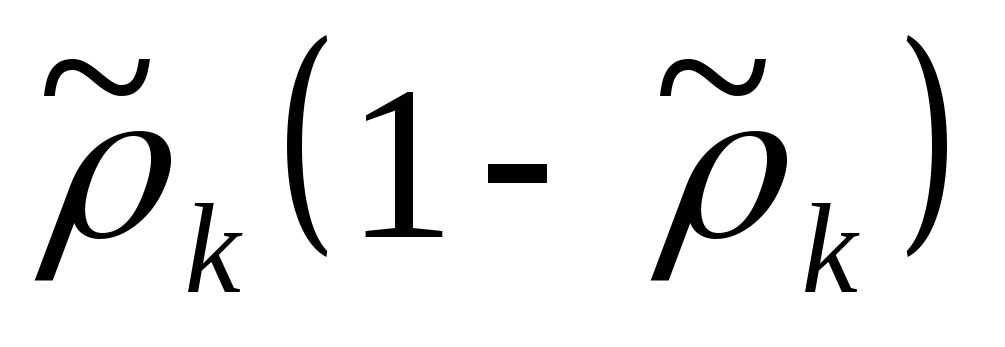
где  — константа сглаживания (01) используемая для получения оценок вектора вероятностей.

Возможны два варианта: в первом варианте пределы классов заданы так, что может быть или очень большим (около 1) или очень маленьким (около 0). Тогда дисперсия компонент вектора вероятностей будет небольшой. Если форма распределения меняется со временем, большое значение компонента сглаживания может быть использована, чтобы устранить влияние “старой” информации.

Во втором варианте распределение вероятностей постоянно во времени и нет необходимости “взвешивать” старую информацию. Малое значение компоненты сглаживания, может использовать меньшие интервалы классов с не очень большими вероятностями. Вероятностная модель оперирует последовательностью наблюдений с учетом их распределения и игнорирует последовательность этой информации уже непосредственно во времени. Поэтому вектор вероятностей , который служит текущей оценкой вероятностей n отдельных событий, является оценкой этих вероятностей в будущем. Последовательность наблюдений может быть представлена как временной ряд х(t), где x измерен по некоторой шкале есть min и max возможных значений наблюдений.

Пусть x случайная величина с ожиданием m и конечной дисперсией . Тогда сумма n случайных выборок будет нормально распределена со средним nm и дисперсией и вероятности как сумма точек наблюдений будут распределены нормально.

Пусть случайная величина Х распределенная между нулем и единицей. Введем функцию f(x) =

если Yn — сумма N случайных выборок, тогда функция распределения этих сумм будет

где 0yN. Находим среднее значение и дисперсию для величины y.

Yp является точкой распределения и ее можно выразить через среднюю и дисперсную распределения

, где Kp — некоторый множитель, учитывающий число степеней свободы распределения.

Данное управление может служить основой оценок для вероятностной модели. При достаточном количестве исходной информации вероятностная модель может дать вполне надежный прогноз. Недостатком является требование достаточно большого количества наблюдений и назначение начального распределения, что может привести к неправильным оценкам.

Экстраполяция базируется на допущениях: 1) развитие явления может быть с достаточным основанием охарактеризовано плановой траекторией-трендом; 2) общие условия, определяющие тенденцию развития в прошлом, не претерпят существенных изменений в будущем. Недостатки данного метода: 1) он исходит из прошлого и настоящего и поэтому накапливаются погрешности; 2) необходимый выбор периода упреждения прогноза. Положительные рез-ты метод дает на 1-2 года, дальше будут ошибки; 3) практическая невозможность получения статистическими методами кривой требуемой формы. Поэтому, чтобы предупредить ошибки в прогнозе, метод экстраполяции следует сочетать с другими методами прогнозирования.

Метод экстраполяции применяется при стабильности системы, устойчивости явлений, когда динамика процессов, показателей в перспективе опред-ся тенденциями их изменения в прошедшем периоде. Предполагается, что развитие идет непрерывно, гладко, силы прошлого в состоянии контролировать будущее. Прогноз становится проекцией прошлого в будущее.

Источник

Оптимизация сетевых моделей по времени и стоимости

В предыдущих параграфах рассматривались вопросы оптимизации сете­вых графиков с точки зрения приведения параметров к какому-либо одно­му заданному ограничению.

Значительный интерес представляет оптимизация сетевых графиков по времени и стоимости, в процессе которой решается вопрос, как уло­житься в заданные ограничения по времени с минимальными дополни­тельными затратами. Оптимизация по времени и стоимости осуществля­ется с помощью метода РЕRТ/СOSТ.

Например, известно, что если сокращается продолжительность строитель­ства, то при одновременном снижении накладных расходов прямые рас­ходы возрастают. Функциональная зависимость между продолжительно­стью работ и их стоимостью пока точно не определена. Поэтому рассмот­рим зависимость «время—стоимость» (с учетом прямых затрат), которая может быть определена условно.

Графически зависимость продолжительности работ от их стоимости изоб­ражена на рисунке 45.

А зависимость

50 Фактическая В

2 4 6 8 10 12 14 16 18 20 22 24

Рисунок 45 — Зависимость продолжительности работ от их стоимости

Как видно из рисунка, точка А соответствует наикратчайшему сроку вы­полнения данного проекта, т.е. сроку, при котором все работы проводятся в предельно сжатые сроки.

Точка В соответствует нормальной продолжительности работ.

Затраты в точке А, так же как срок, считаются предельными: их дальней­шее увеличение лишь в очень незначительной степени повлияет на сокра­щение сроков. Затраты в точке Вявляются нормальными.

Прямая линия, соединяющая точки А и В, точнее степень наклона этой прямой, и является характеристикой изменения величины прямых затрат при изменении продолжительности работ на единицу времени. Величина наклона для каждой единицы времени является величиной постоянной, так как мы приняли линейную зависимость между продолжительностью и стоимостью работ. (В действительности эта величина является условной. Фактическая зависимость изображена на рисунке 45 кривой, соединяющей точки А и В.)

Величина наклона прямой определяется дробью, в числителе которой — разность между затратами в предельном и нормальном режимах, а в знаменателе — разность между продолжительностью работ в нормальном и предельном режимах. Для прямой, изображенной на рисунке 45, эта величина составит:

(70 — 60): (24 — 16) = 1,25 (тыс. руб./день).

Для проведения оптимизации необходимо по каждой работе определить предельные и нормальные сроки выполнения, а также предельные и нор­мальные величины затрат. После этого методом последовательного при­ближения достичь заданного предельного срока за счет сокращения про­должительности критических работ, имеющих наименьшую величину удо­рожания.

Выберите один или несколько правильных ответов

1. Оптимизация сетевой модели может проводиться:

г) по информационным ресурсам;

д) по параметрам «время—стоимость»;

е) по параметрам «цена—качество».

2. Оптимизация сетевой модели может предполагать:

а) приведение параметров сетевого графика к существующим ограничениям;

б) повышение качества производимой продукции;

в) повышение заработной платы исполнителей;

г) перепланирование работ по проекту;

д) изменение топологии сетевого графика.

3. Главный вид оптимизации — это оптимизация:

4. Оптимизация сетевого графика по времени производится в случаях:

а) когда проект не укладывается в директивные сроки;

б) когда проект заканчивается раньше запланированного времени;

в) когда имеются бюджетные ограничения.

5. Методами оптимизации сетевого графика по времени являются:

а) сокращение продолжительности критических работ;

б) перенос директивных сроков на более позднее время;

в) изменение топологии сетевого графика за счет изменения технологии работ.

6. Сократить продолжительность проекта путем расчленения и запараллеливания критических работ можно:

7. Путем расчленения и запараллеливания критических работ осуще­ствляется оптимизация сетевой модели:

8. Оптимизация сетевых графиков по трудовым ресурсам осуществля­ется в случаях:

а) когда есть необходимость равномерной и ритмичной загрузки персонала;

б) когда есть ограничения на использование трудовых ресурсов;

в) когда трудовых ресурсов недостаточно для выполнения проекта.

9. Перераспределение ресурсов происходит за счет использования:

10. Метод РЕRТ/СОSТ используется для:

а) оптимизации загрузки трудовых ресурсов;

б) оптимизации по времени и стоимости;

в) оптимизации по материальным ресурсам.

11. При использовании метода РЕRТ/СОSТ продолжительность проекта можно сократить за счет:

а) увеличения бюджета проекта;

б) сокращения бюджета проекта;

в) привлечения дополнительных ресурсов.

12. При сокращении стоимости работ по методу РЕRТ/СОSТ про­исходит:

а) увеличение продолжительности проекта;

б) увеличение объема работ;

в) увеличение объема вовлекаемых ресурсов.

13. Фактическая зависимость между стоимостью и продолжительностью

работ по проекту имеет вид:

14. Метод РЕRТ/СОSТ можно использовать в случаях:

а) когда необходимо сократить продолжительность и есть возможность увеличить бюджет;

б) когда необходимо сократить бюджет и есть возможность увеличить продолжительность работ;

в) когда есть возможность увеличить как бюджет, так и продолжительность работ по проекту.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник