Оптимизация сетевой модели по трудовым ресурсам

Оптимизация сетевой модели по трудовым ресурсам.

После расчета сетевой модели и приведения ее к директивной продолжительности возникает задача оптимизации сетевой модели по трудовым ресурсам, заключающееся в обеспечении равномерного потребления этих ресурсов на протяжении всего периода выполнения комплекса работ (выравнивание графика потребления трудовых ресурсов). Основным методом решения этой задачи является сдвиг части работ из положения соответствующего наиболее раннему времени его начала на более позднее время в пределах позднего резерва. Т.о. задача оптимизации сетевой модели по трудовым ресурсам сводится к составлению такого расписания работ, которое обеспечивает наибольшую равномерность графика трудовых ресурсов.

Построение графика трудовых ресурсов по дням работы.

Для построения графика потребностей трудовых ресурсов необходимо построить линейную диаграмму обеспечения трудовых ресурсов . Для построения линейной диаграммы проводят вертикальную и горизонтальную оси . Горизонтальную ось делят на равные отрезки по числу дней критического пути. Вертикальная ось делится на число отрезков по числу работ сетевой модели с учетом фиктивных работ в виде точек.

Правила построения линейной диаграммы:

1. Построение линейной диаграммы начинается снизу вверх в порядке возрастания номеров начала событий для работ.
2. Если из события выходит несколько работ, то они располагаются в порядке возрастания полных резервов времени.
3. Работы на линейной диаграмме имеют ту же нумерацию, что на сетевой модели.
4. Над каждой работой указывают численность персонала для ее выполнения.
5. По линейной диаграмме подсчитывается ежедневная суммарная численность исполнителей, которая записывается по соответствующим дням в горизонтальной строке под линейной диаграммой. И строиться график потребностей трудовых ресурсов по дням работы.

Последовательность формирования столбца нарастающих сумм:

1. Составляется первый столбец и суммируются численности персонала в дни резерва работы.
2. Составляется второй столбец из суммарной численности персонала начиная с первого дня исходного положения работы без численности исполнителя данной работы до заполнения всех строк первого столбца.
3. Составляется третий столбец из разности значений численности первого и второго столбцов каждой строки.
4. Составляется четвертый столбец (последний)-столбец нарастающих сумм. В первую строчку 4-го столбца вносятся значения первой строчки 3 столбца, во вторую строчку алгебраическая сумма чисел, записанных в 1-ой строчке 4-го столбца и 2-ой строчке 3-го столбца и т.д. до заполнения всех строк.
5. Решение вопроса о целесообразности сдвига работ можно получить путем анализа величин, записанных в 4-м столбце.

Источник

Оптимизация сетевой модели по критерию время – число исполнителей

После построения сетевого графика и определения его временных параметров проводят проверку соответствия полученных сроков продолжительности разработки нормативным или директивным срокам. Далее анализируют структуру сетевой модели, выявляя неоднородность напряженности работ проекта.
В настоящее время на практике сетевую модель вначале корректируют по времени, т. е. приводят ее к заданному сроку окончания проекта. Затем приступают к корректировке графика по критерию распределения ресурсов, начиная с трудовых ресурсов.

Минимизация числа исполнителей проекта при сохранении времени его выполнения

• минимизировать количество одновременно занятых исполнителей;
• выровнять потребность в трудовых ресурсах на протяжении всего срока выполнения проекта.

• перемещение работ по оси времени возможно осуществлять только вправо (откладывая их начало);
• работы критического пути трогать нельзя, т. к. это приведет к увеличению срока выполнения всего проекта;
• работы, имеющие свободный резерв времени, можно спокойно перемещать на величину этого резерва;
• перемещение работ, имеющих только полный резерв времени, требует аналогичного сдвига последующих работ;
• передвигаемые работы на линейной диаграмме выделяют, отмечая заметным символом: звездочкой, штрихом, цветом и т.п.

Рис. 1. Пример сетевого графика

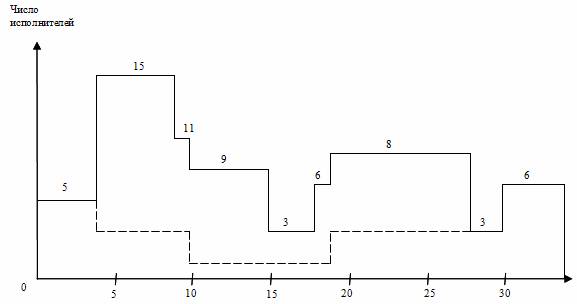
Проведем более детальный анализ линейной диаграммы и карты проекта с целью оптимизации трудовых ресурсов: выравнивая потребность в них на протяжении всего проекта и минимизируя количество одновременно занятых исполнителей. График ежедневной потребности ресурса показывает, что минимальное число исполнителей не может быть меньше 6 человек, что определяется их потребностью для работ критического пути. А 15 исполнителей на участке 5-10 дни проекта является явно завышенным и подлежит коррекции в первую очередь.

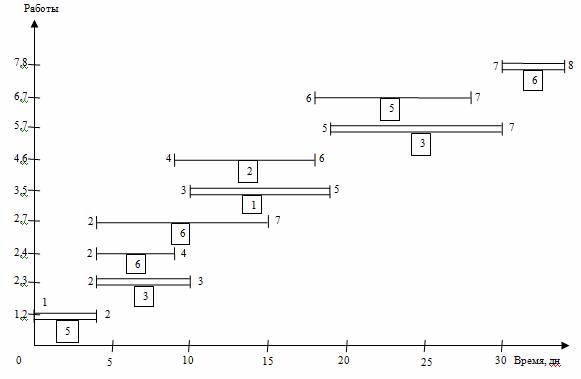
Рис. 2. Линейная диаграмма и карта проекта до оптимизации

15 исполнителей заняты на работах 2,3; 2,4 и 2,7. Работу 2,3 трогать нельзя, т. к. это работа критического пути. Работа 2,4 имеет только полный резерв, но не имеет свободного резерва времени. Работа 2,7 имеет солидный свободный резерв времени и поэтому наиболее предпочтительна для оптимизации. Используем часть свободного резерва, переместив работу 2,7 (5-15 дни) на 5 дней (ее новый срок 10-20 дни). Тем самым максимально необходимое число исполнителей уменьшилось до 9 человек, т.е. задачу минимизации трудовых ресурсов проекта можно принять завершенной.

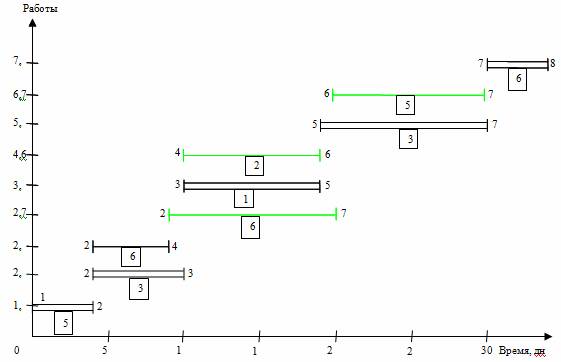
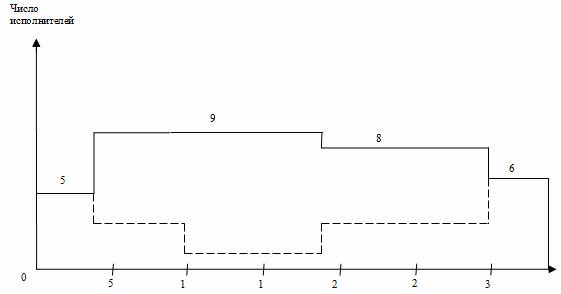
Рис. 3. Линейная диаграмма и карта проекта после оптимизации
Далее решим задачу выравнивания потребности в ресурсах, анализируя интервалы времени, связанные с «провалами» карты проекта. С учетом перемещения работы 2,7 падения спроса на исполнителей в середине проекта (16-18 дни) уже не будет, но он останется ближе к концу проекта (29-30 дни). Чтобы сгладить график загрузки, переместим работу 6,7 (19-28 дни), имеющую свободный резерв времени, на 2 дня (новый срок 21-30 дни). Также для целей выравнивания потребности в трудовых ресурсах переместим работу 4,6 (10-18 дни) на 1 день (11-19 дни).
В итоге оптимизации приходим к линейной диаграмме и карте проекта, представленными на рис. 3. Из графика видно улучшение равномерности загрузки исполнителей: новая ежедневная потребность ресурса составляет от 5 до 9 человек в зависимости от этапа выполнения проекта, резких колебаний занятости нет. Длительность выполнения всего проекта при этом осталась неизменной (34 дня), т. е. необходимое условие оптимизации соблюдено. Видеоинструкция

Источник

Оптимизация сетевой модели по трудовым ресурсам.

После расчета сетевой модели и приведения ее к директивной продолжительности возникает задача оптимизации сетевой модели по трудовым ресурсам, заключающееся в обеспечении равномерного потребления этих ресурсов на протяжении всего периода выполнения комплекса работ (выравнивание графика потребления трудовых ресурсов). Основным методом решения этой задачи является сдвиг части работ из положения соответствующего наиболее раннему времени его начала на более позднее время в пределах позднего резерва. Т.о. задача оптимизации сетевой модели по трудовым ресурсам сводится к составлению такого расписания работ, которое обеспечивает наибольшую равномерность графика трудовых ресурсов.

Построение графика трудовых ресурсов по дням работы.

Для построения графика потребностей трудовых ресурсов необходимо построить линейную диаграмму обеспечения трудовых ресурсов . Для построения линейной диаграммы проводят вертикальную и горизонтальную оси . Горизонтальную ось делят на равные отрезки по числу дней критического пути. Вертикальная ось делится на число отрезков по числу работ сетевой модели с учетом фиктивных работ в виде точек.

Правила построения линейной диаграммы:

1. Построение линейной диаграммы начинается снизу вверх в порядке возрастания номеров начала событий для работ.
2. Если из события выходит несколько работ, то они располагаются в порядке возрастания полных резервов времени.
3. Работы на линейной диаграмме имеют ту же нумерацию, что на сетевой модели.
4. Над каждой работой указывают численность персонала для ее выполнения.
5. По линейной диаграмме подсчитывается ежедневная суммарная численность исполнителей, которая записывается по соответствующим дням в горизонтальной строке под линейной диаграммой. И строиться график потребностей трудовых ресурсов по дням работы.

Последовательность формирования столбца нарастающих сумм:

1. Составляется первый столбец и суммируются численности персонала в дни резерва работы.
2. Составляется второй столбец из суммарной численности персонала начиная с первого дня исходного положения работы без численности исполнителя данной работы до заполнения всех строк первого столбца.
3. Составляется третий столбец из разности значений численности первого и второго столбцов каждой строки.
4. Составляется четвертый столбец (последний)-столбец нарастающих сумм. В первую строчку 4-го столбца вносятся значения первой строчки 3 столбца, во вторую строчку алгебраическая сумма чисел, записанных в 1-ой строчке 4-го столбца и 2-ой строчке 3-го столбца и т.д. до заполнения всех строк.
5. Решение вопроса о целесообразности сдвига работ можно получить путем анализа величин, записанных в 4-м столбце.

Если в 4-ом столбце все числа положительны, то сдвиг данной работы нецелесообразен. Если же в нем окажутся отрицательные величины, то необходимо зафиксировать отрицательное число с наибольшей абсолютной величиной и определить порядковый номер строки, в которой это число появилось в первый раз. Эту работу целесообразно сдвинуть вправо на количество дней, равное порядковому номеру данной строки. Следуя данной последовательности, построим линейную диаграмму и в последствии график потребностей трудовых ресурсов. Заключение. В данной работе было проведено построение и расчет сетевых графиков ремонта котло- и турбоагрегата, их оптимизация, а также построены линейные диаграммы обеспечения трудовых ресурсов и графики потребностей трудовых ресурсов.

Источник