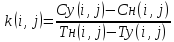8.3. Оптимизация сетевых моделей
8.3.1. Оптимизация использования ресурса рабочей силы
При оптимизации использования ресурса рабочей силы сетевые работы чаще всего стремятся организовать таким образом, чтобы:
− количество одновременно занятых исполнителей было минимальным;
− выровнять потребность в людских ресурсах на протяжении срока выполнения проекта.
Для проведения подобных видов оптимизации необходим график загрузки.
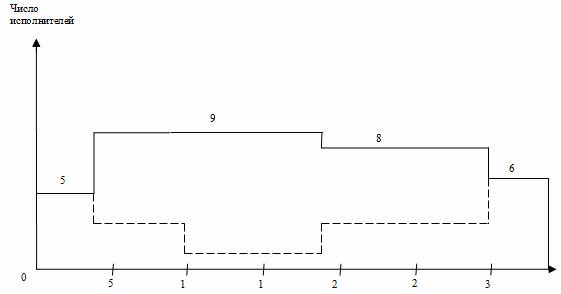
На графике загрузки по горизонтальной оси откладывается время, например в днях, по вертикальной – количество человек, занятых работой в каждый конкретный день. Для построения графика загрузки необходимо:
− на графике привязки над каждой работой написать количество ее исполнителей;
− подсчитать количество работающих в каждый день исполнителей и отложить на графике загрузки.
Для удобства построения и анализа, графики загрузки и привязки следует располагать один над другим.
Пример построения графика загрузки. Описанные виды оптимизации могут быть выполнены с помощью сдвига работ, который осуществляется за счет резервов времени: свободного или полного. После сдвига работы, работники выполняют ее уже в другие дни, и поэтому для каждого дня изменяется количество исполнителей занятых одновременно.
Резервы работ можно определить без специальных расчетов, только с помощью графика привязки.
Различие в использовании свободных и полных резервов заключается в том, что при сдвиге работы, с использованием свободного резерва, моменты начала следующих за ней работ остаются неизменными (т.е. последующие работы не сдвигаются). При сдвиге работы, с использованием полного резерва, все последующие работы сдвигаются.
8.3.2. Оптимизация типа «время – затраты»
Целью оптимизации по критерию «время – затраты» является сокращение времени выполнения проекта в целом. Эта оптимизация имеет смысл только в том случае, когда длительность выполнения работ может быть уменьшена за счет задействования дополнительных ресурсов, что влечет повышение затрат на выполнение работ. Для оценки величины дополнительных затрат, связанных с ускорением выполнения той или иной работы, используются либо нормативы, либо данные о выполнении аналогичных работ в прошлом.
Исходными данными для проведения оптимизации являются:
− Tн(i,j) – нормальная длительность работы;
− Tу(i,j) – ускоренная длительность;
− Cн(i,j) – затраты на выполнение работы в нормальный срок;
− Cу(i,j) – затраты на выполнение работы в ускоренный срок.
Т.о. каждая работа имеет некоторый максимальный запас времени для сокращения своей длительности Zmax(i,j) =Tн(i,j) −Tу(i,j).
Для анализа сетевой модели в данном виде оптимизации используется коэффициент нарастания затрат (коэффициент ускорения)
который имеет смысл (Дополнительный вопрос: какой смысл?) затрат денежных средств для сокращения длительности выполнения работы (i,j) на один день.
Оптимизация критического пути. Оптимизация критического пути заключается в улучшении его в соответствии с принятым критерием.
В принципе, этими критериями могут быть: время, стоимость, людские и материальные ресурсы и др.
В настоящее время оптимизация сетевых графиков выполняется в основном только по критерию времени.
Оптимизация может производиться с различными целями:
1. если критический путь со временем T превышает заданные сроки T 0, то оптимизация по времени заключается в сокращении критического пути.
Для сокращения критического пути, естественно, имеет смысл форсировать критические работы. Их можно ускорить, например:
1. за счёт дополнительных сил и средств;
2. за счёт переброски сил и средств с некритических работ на критические.
Если используется пункт 1, то возникает типичная задача исследования операций: какие дополнительные средства x 1, x 2 . x n и в какие критические работы нужно вложить, чтобы критический путь T ≤ T 0, а расход дополнительных средств был минимальным.
Если используется пункт 2, т.е. для оптимизации критического пути перебрасываются имеющиеся средства с некритических работ на критические.
Общая схема проведения оптимизации:
1. проводится расчет сети исходя из нормальных длительностей работ;
2. определяется сумма затрат на выполнение всего проекта при нормальной продолжительности работ;
3. рассматривается возможность сокращения продолжительности проекта.
Поскольку этого можно достичь за счет уменьшения продолжительности какой-либо критической работы, то только такие операции подвергаются анализу;
3.1. для сокращения выбирается критическая работа с min коэффициентом нарастания затрат k(i,j), у которой есть запас сокращения времени;
3.2. определяется время Δt(i,j), на которое необходимо сжать длительность работы (i,j). При этом руководствуются следующими соображениями;
3.2.1. максимально возможный запас времени для сокращения работы на текущий момент Z(i,j) ограничивается значением Tу(i,j), т.е.
Z(i,j)=tт(i,j)−Tу(i,j), где tт (i,j) — текущее время выполнения работы
(tт(i,j) =Tн(i,j) только для работ еще не подвергшихся сокращению);
3.2.2. кроме критического пути длительностью Tкр в сети есть подкритический путь длительностью Tп . Критический путь нельзя сократить больше, чем ΔT=Tкр−Tп, поскольку в этом случае критический путь перестанет быть таковым, а подкритический путь наоборот станет критическим;
3.2.3. исходя из вышесказанного, время сокращения длительности выбранной работы (i,j) равно Δt=tт (i,j)−min[Z(i,j),ΔT]. Другими словами, если разность между длительностью критического и подкритического путей ΔT меньше текущего запаса времени сокращения работы Z(i,j), то имеет смысл сокращать работу только на ΔT дней. В противном случае можно сокращать работу полностью на величину Z(i,j);
4. в результате сжатия критической операции получают новый календарный план, возможно с новыми критическими и подкритическими путями, и обязательно с новыми более высокими затратами на выполнение проекта. Это происходит вследствие удорожания ускоренной работы. Общая стоимость проекта увеличивается на ΔC = k(i, j)Δt;
5. переход на шаг 3, который повторяется до тех пор, пока стоимость проекта уменьшается.
В результате оптимизации строится график «Время – затраты».
Под параметрами работ Cн(i,j) и Cу(i,j) понимаются так называемые прямые затраты, т.е. косвенные затраты типа административно-управленческих во внимание не принимаются. Однако их влияние учитывается при выборе окончательного календарного плана проекта. В отличие от прямых затрат косвенные затраты при уменьшении продолжительности проекта убывают, что показано на графике. Оптимальный календарный план соответствует минимуму общих затрат (точка А).
8.3.3. Неопределенность времени выполнения операций
В описанных методах анализа сетей предполагалось, что время выполнения работ точно известно, однако на практике сроки выполнения работ обычно довольно неопределенны. В таких случаях обычно используют экспертные оценки минимальной (a), максимальной (b) и наиболее вероятной длительности (m) работ для расчета их ожидаемой продолжительности.
Данный метод основан на предположении, что время выполнения каждой отдельной работы аппроксимируется β – распределением. При таком подходе можно оценивать вероятности наступления событий в пределах их ранних и поздних сроков, вероятность завершения проекта к заранее установленной дате и другие вероятностные характеристики.
Оптимизация сетевой модели по критерию время – число исполнителей
После построения сетевого графика и определения его временных параметров проводят проверку соответствия полученных сроков продолжительности разработки нормативным или директивным срокам. Далее анализируют структуру сетевой модели, выявляя неоднородность напряженности работ проекта.
В настоящее время на практике сетевую модель вначале корректируют по времени, т. е. приводят ее к заданному сроку окончания проекта. Затем приступают к корректировке графика по критерию распределения ресурсов, начиная с трудовых ресурсов.
Минимизация числа исполнителей проекта при сохранении времени его выполнения
- минимизировать количество одновременно занятых исполнителей;
- выровнять потребность в трудовых ресурсах на протяжении всего срока выполнения проекта.
- перемещение работ по оси времени возможно осуществлять только вправо (откладывая их начало);
- работы критического пути трогать нельзя, т. к. это приведет к увеличению срока выполнения всего проекта;
- работы, имеющие свободный резерв времени, можно спокойно перемещать на величину этого резерва;
- перемещение работ, имеющих только полный резерв времени, требует аналогичного сдвига последующих работ;
- передвигаемые работы на линейной диаграмме выделяют, отмечая заметным символом: звездочкой, штрихом, цветом и т.п.
Рис. 1. Пример сетевого графика
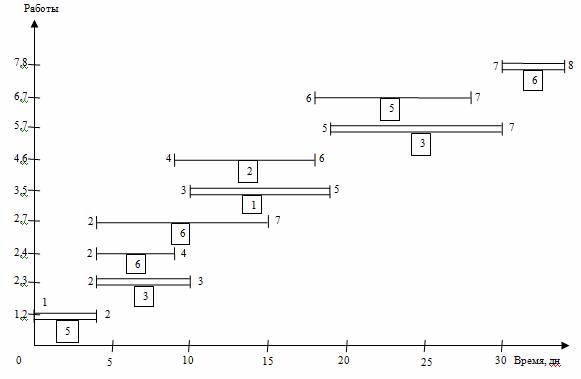
Проведем более детальный анализ линейной диаграммы и карты проекта с целью оптимизации трудовых ресурсов: выравнивая потребность в них на протяжении всего проекта и минимизируя количество одновременно занятых исполнителей. График ежедневной потребности ресурса показывает, что минимальное число исполнителей не может быть меньше 6 человек, что определяется их потребностью для работ критического пути. А 15 исполнителей на участке 5-10 дни проекта является явно завышенным и подлежит коррекции в первую очередь.
Рис. 2. Линейная диаграмма и карта проекта до оптимизации
15 исполнителей заняты на работах 2,3; 2,4 и 2,7. Работу 2,3 трогать нельзя, т. к. это работа критического пути. Работа 2,4 имеет только полный резерв, но не имеет свободного резерва времени. Работа 2,7 имеет солидный свободный резерв времени и поэтому наиболее предпочтительна для оптимизации. Используем часть свободного резерва, переместив работу 2,7 (5-15 дни) на 5 дней (ее новый срок 10-20 дни). Тем самым максимально необходимое число исполнителей уменьшилось до 9 человек, т.е. задачу минимизации трудовых ресурсов проекта можно принять завершенной.
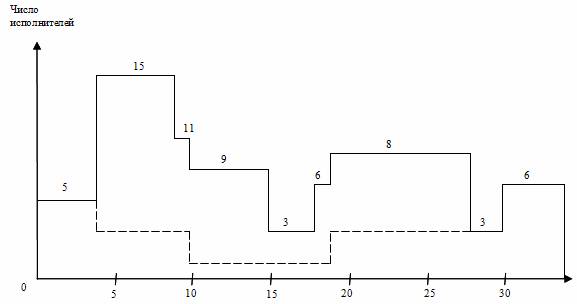
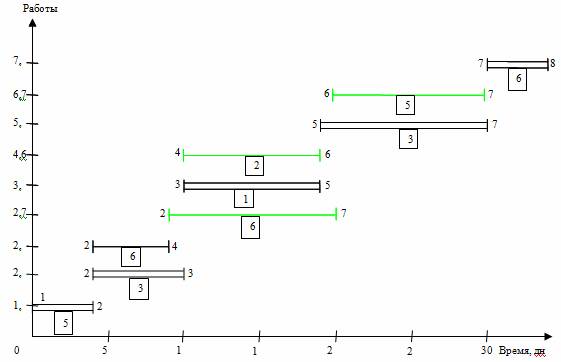
Рис. 3. Линейная диаграмма и карта проекта после оптимизации
Далее решим задачу выравнивания потребности в ресурсах, анализируя интервалы времени, связанные с «провалами» карты проекта. С учетом перемещения работы 2,7 падения спроса на исполнителей в середине проекта (16-18 дни) уже не будет, но он останется ближе к концу проекта (29-30 дни). Чтобы сгладить график загрузки, переместим работу 6,7 (19-28 дни), имеющую свободный резерв времени, на 2 дня (новый срок 21-30 дни). Также для целей выравнивания потребности в трудовых ресурсах переместим работу 4,6 (10-18 дни) на 1 день (11-19 дни).
В итоге оптимизации приходим к линейной диаграмме и карте проекта, представленными на рис. 3. Из графика видно улучшение равномерности загрузки исполнителей: новая ежедневная потребность ресурса составляет от 5 до 9 человек в зависимости от этапа выполнения проекта, резких колебаний занятости нет. Длительность выполнения всего проекта при этом осталась неизменной (34 дня), т. е. необходимое условие оптимизации соблюдено. Видеоинструкция