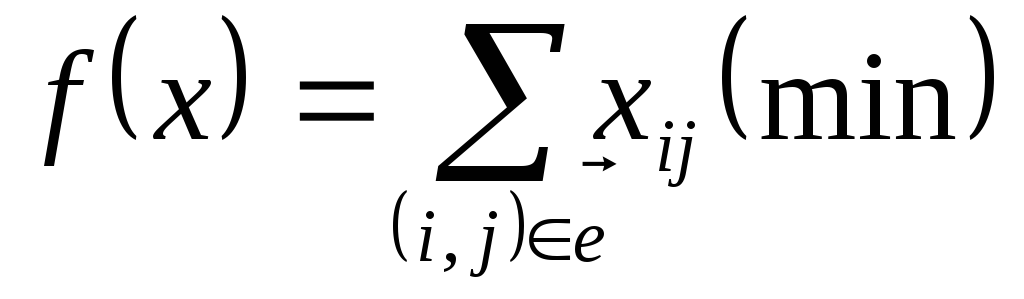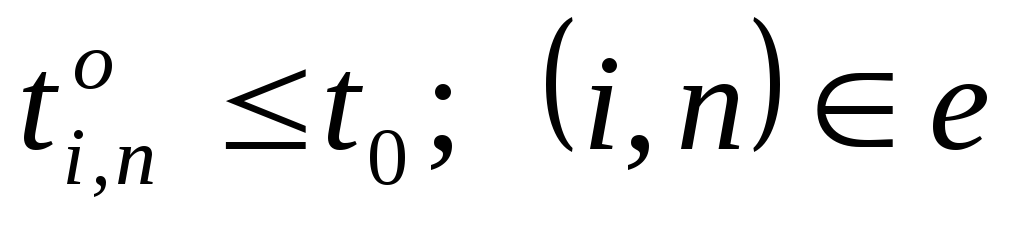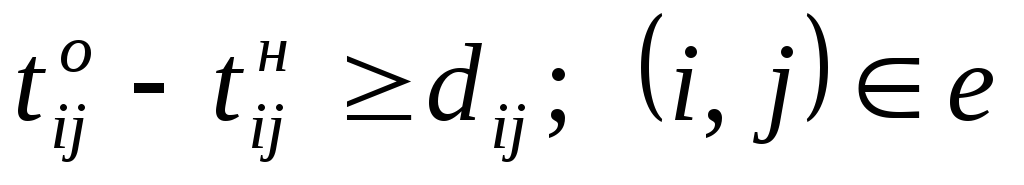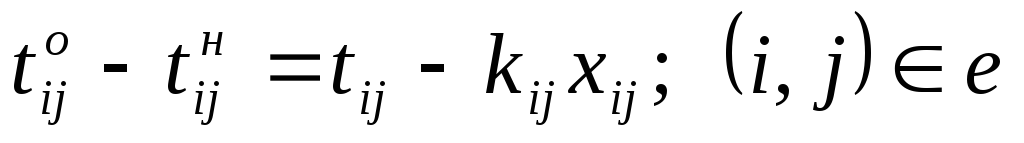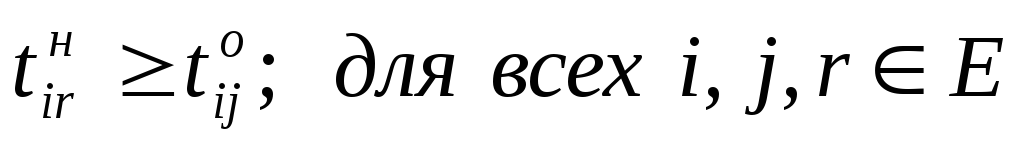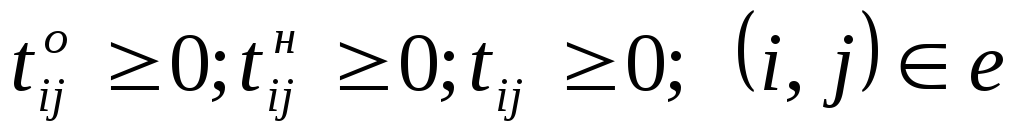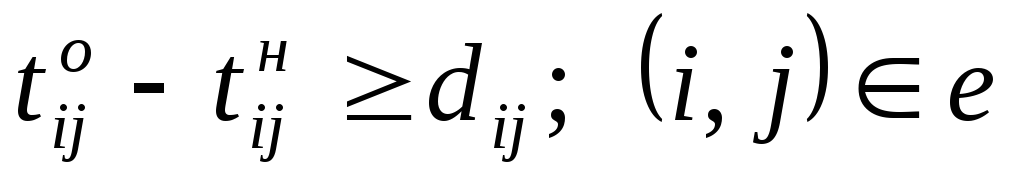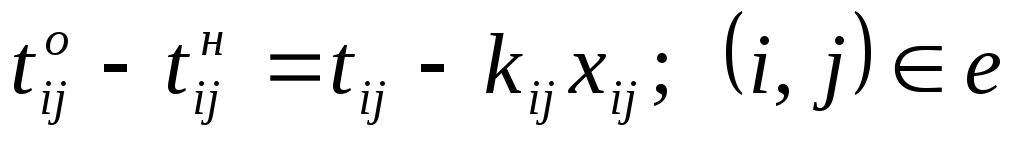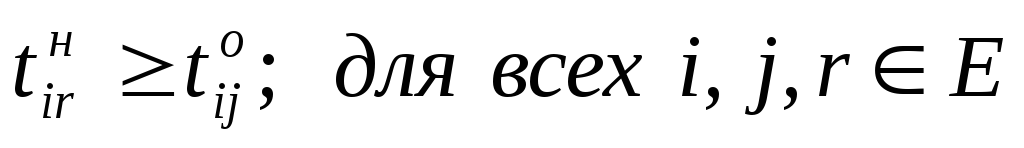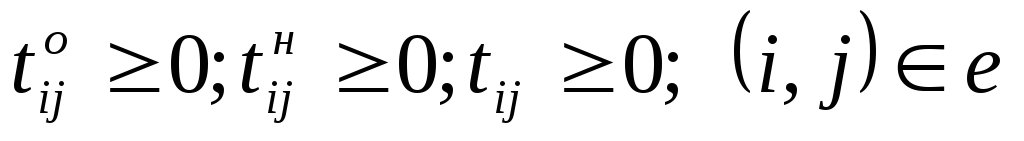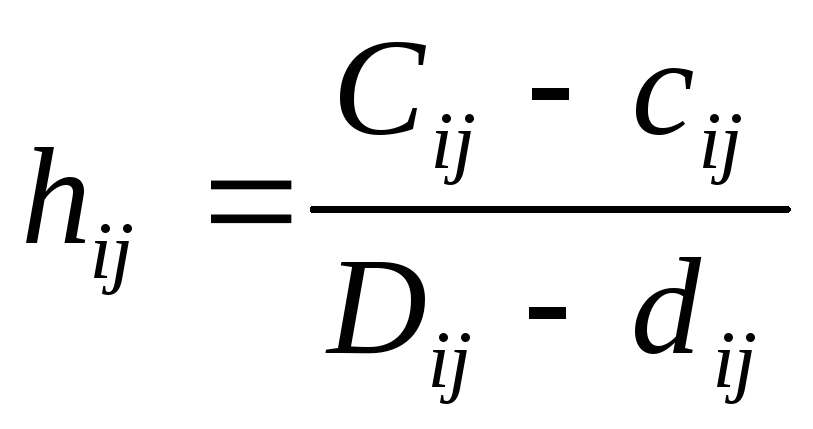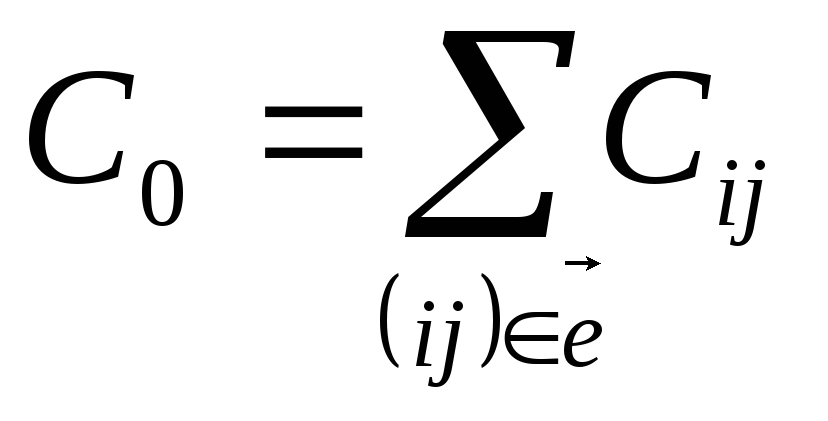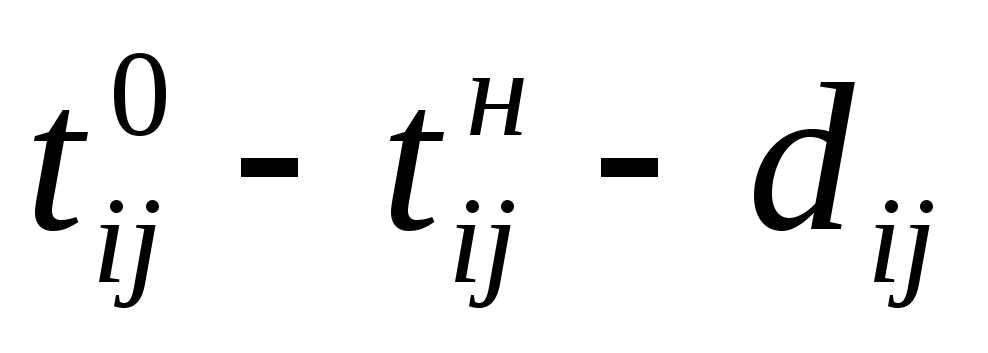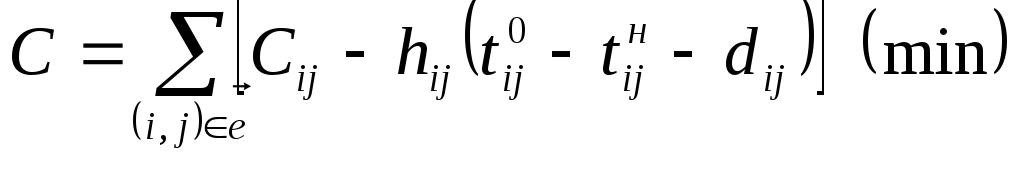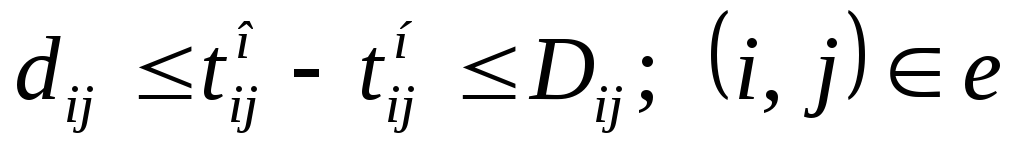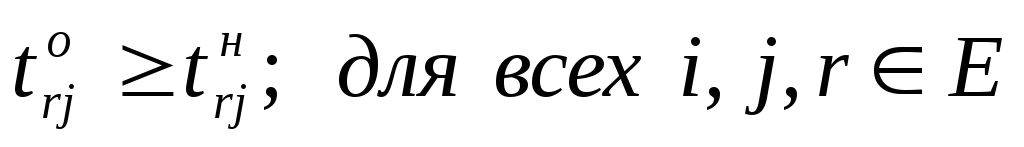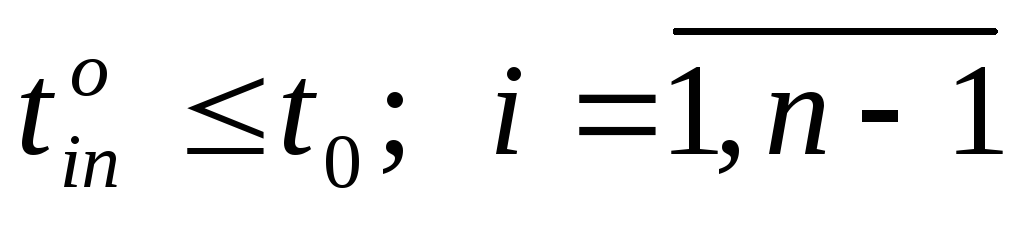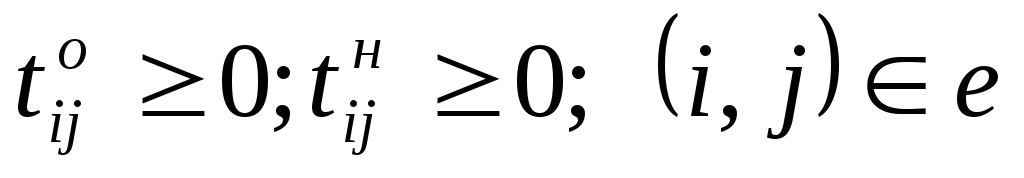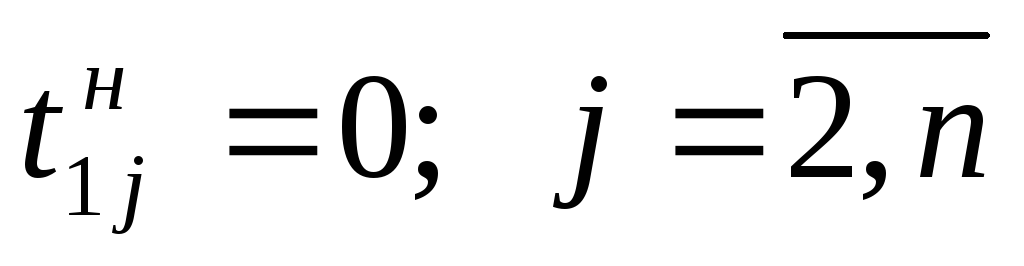Оптимизация сетевых моделей это

6 Виды и сущность оптимизации сетевых моделей

Расчет параметров сетевого графика проекта позволяет выявить критические работы, определяющие ход выполнения всего комплекса работ, продолжительность его реализации, ре­зервы времени событий и работ и проанализировать, можно ли его использовать в качестве плана выполнения работ. Чаще всего требуется улучшение сетевого графика с учетом сроков выполнения работ и рационального использования материаль­ных, трудовых и денежных ресурсов, т. е. требуется его опти­мизация. Рассмотрим некоторые математические модели оп­тимизационных задач на сетевых графиках.

6.1 Оптимизация проекта по времени. Пусть задан срок выполнения проекта t₀, а расчетное t_кр > t₀. В этом случае оптимизация комплекса работ сводится к сокра­щению продолжительности критического пути, которое может быть осуществлено либо за счет перераспределения внутрен­них резервов, либо за счет привлечения дополнительных средств.

Сокращение времени завершения проекта, как правило, связано с привлечением дополнительных средств (количес­тво рабочих, сверхурочное время). Рассмотрим два примера постановки задачи оптимизации проекта по времени с при­влечением дополнительных средств.

Задача 1 заключается в определении величины дополнитель­ных вложений х_ij в отдельные работы проекта с тем, чтобы общий срок его выполнения не превышал заданной величины t₀, а сум­марный расход дополнительных средств В был минимальным.

Задан сетевой график G = (Е,) выполнения проекта, где Е — множество событий, а — множество работ. Продолжительность каждой работы равна t_ij. Известно, что вложение дополнительных средств х_ij в работу (i, j) сокра­щает время ее выполнения от t_ij до t‘_ij, причем , гдеk_ij – технологические коэффициенты использования дополнительных средств. Но сокращение продолжительности работы не беспредельно, для каждой работы существует минимально возможное время ее выполнения d_ij.

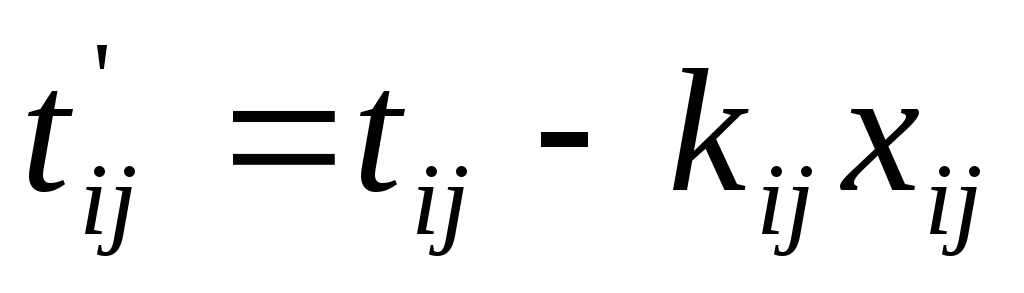
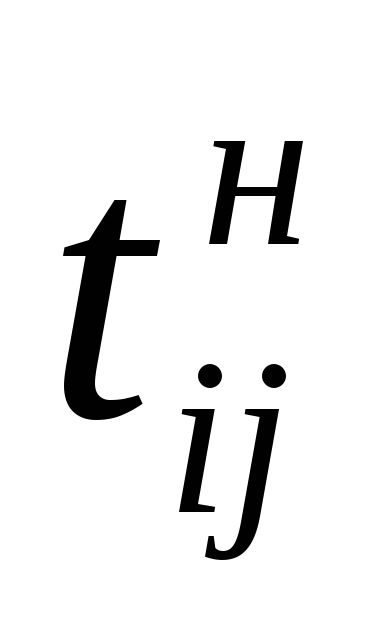
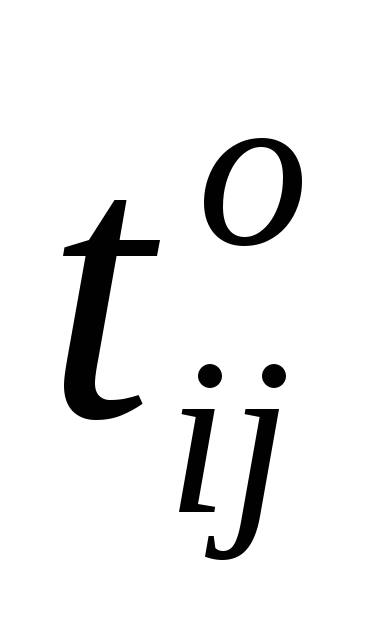
Требуется определить количество дополнительных средств x_ij, которые необходимо вложить в работы (i, j), а также время начала и окончаниявы­полнения этих работ, что­бы проект был выполнен в срокt₀, а суммарные дополнительные затраты были минимальными.

Математически условия задачи можно записать следую­щим образом:

; (6.3)

; (6.4)

; (6.5)

; (6.6)

; (6.7)

. (6.8)

Ограничение (6.4) определяет время завершения проекта, оно должно быть не больше заданного t_о. Ограничения (6.5) показывают, что продолжительность каждой работы должна быть не менее минимально возможной ее продолжительности. Ограничения-равенства (6.6) показывают зависимость продол­жительности каждой работы от вложенных в нее дополнитель­ных средств. Ограничения (6.7) обеспечивают выполнение ус­ловий предшествования работ: время начала выполнения каж­дой работы должно быть не меньше времени окончания непос­редственно предшествующих ей работ. Ограничение (6.8) — условие неотрицательности.

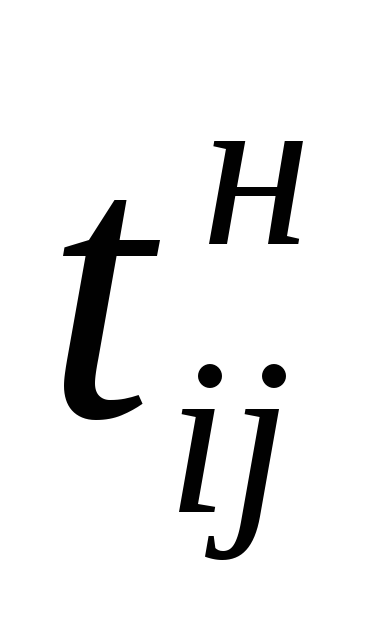
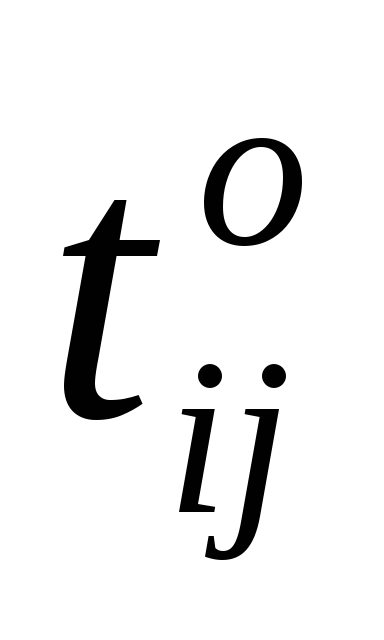
Задача 2 заключается в сокращении срока выполнения проекта, насколько это возможно за счет вложения суммы дополнительных средств, не превышающей В. Время выполне­ния каждой работы должно быть не меньше минимально воз­можного времени d_ij. Необходимо определить время начала и окончания каждой работы и величину дополнительных средств х_ij, которые нужно выделить на ускорение выполне­ния работы (i,j).

Математическая модель задачи 2 имеет вид:

;(6.9)

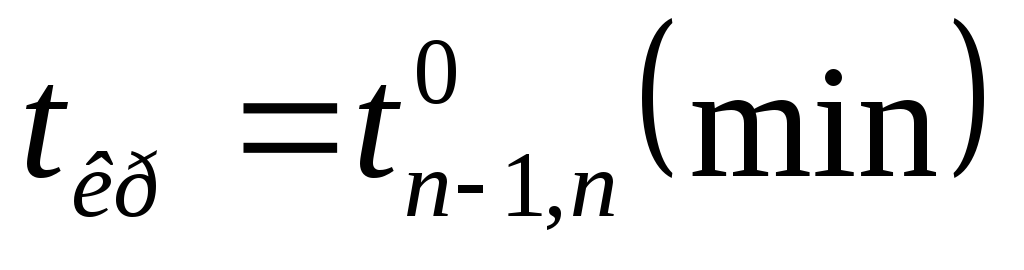
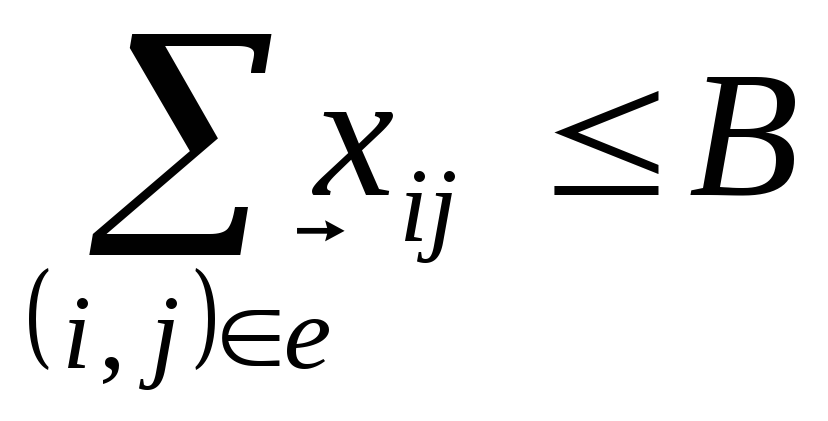
; (6.10)

; (6.11)

; (6.12)

. (6.13)

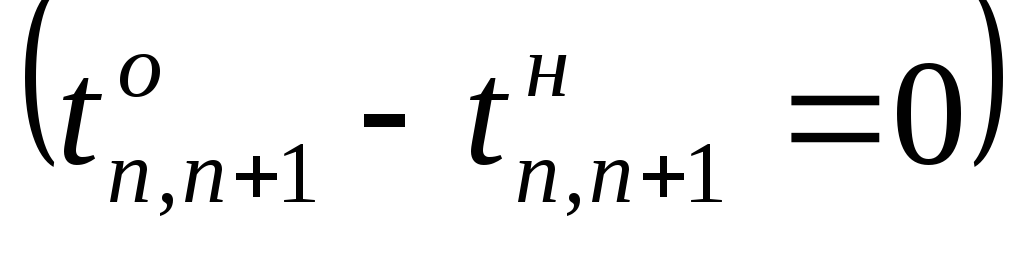
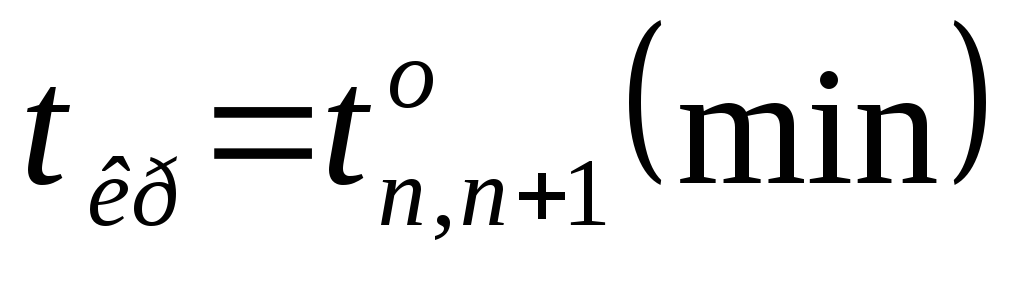
Смысл ограничений (6.10) – (6.13) аналогичен соответствующим огра­ничениям постановки задачи 1 (6.4) — (6.8). Если в последнее событие сети n входят сразу несколько работ, то необходимо добавить фиктивную работу (n, n+1), время выполнения которой равно нулю . Тогда целевая функция запи­шется так.

6.2 Оптимизация проекта по стоимости. В общем случае стоимость выполнения работы зависит от ее продолжительности. Продолжительность каждой работы может изменяться между двумя границами d_ij и D_ij, определя­емыми техническими или экономическими соображениями. Если D_ij — нормальная продолжительность, ей соответствует минимальная стоимость с_ij выполнения работы (i, j); если d_ij — минимально возможная (экстренная) продолжитель­ность работы, при этом стоимость работы будет максимальной C_ij. Если при планировании проекта для каждой работы будет взята ее нормальная (наибольшая) длительность D_ij, то стои­мость проекта будет минимальной. Если для каждой работы взять ее ускоренную, минимально возможную продолжитель­ность d_ij, то получим срочный план. Стоимость выполнения проекта в этом случае будет максимальной.

Зависимость стоимости от продолжительности работы не­линейна, но для упрощения оптимизационных расчетов предполагают, что уменьшение продолжительности работы пропорционально возрастанию ее стоимости. Тогда в расчете на единицу времени дополнительные затраты на сокращение продолжительности работы будут равны

. (6.14)

Рассмотрим оптимизацию комплекса работ по стоимости при фиксированном сроке выполнения.

Предполагается, что все работы выполняются в срочном режиме и исходная стоимость проекта максимальна. Необходимо минимизировать стоимость про­екта при фиксированном сроке его завершенияt₀ за счет уве­личения времени выполнения отдельных работ.

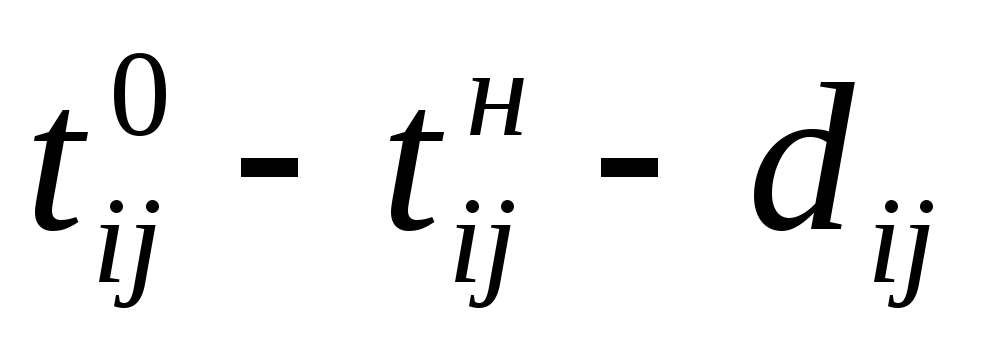
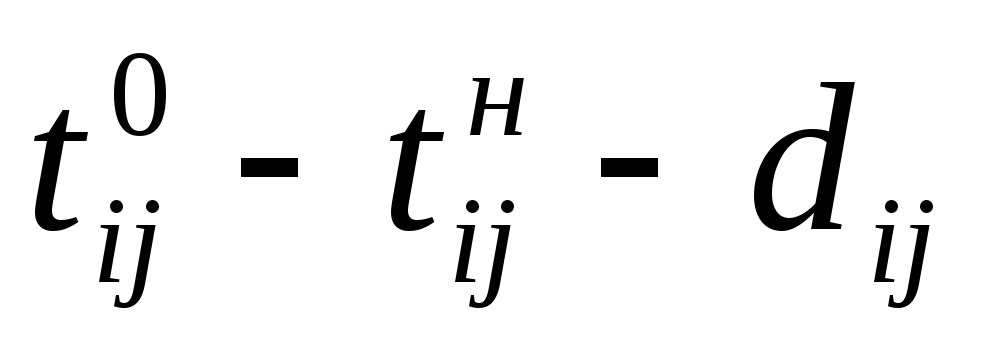
Увеличение продолжительности работы (i, j) по сравне­нию с минимальным сроком выполнения на () вызовет экономию средств на величинуh_ij () , a стоимость выполнения работы станет равна

C = C_ij — h_ij ().(6.15)

Если t₀ = t_кp, то оптимизация осуществляется за счет увели­чения продолжительности некритических работ; если t_кр t₀, — то за счет всех работ комплекса.

Математическая запись задачи:

; (6.16)

; (6.17)

; (6.18)

; (6.19)

; (6.20)

. (6.21)

Здесь 1 — номер исходного события, n — номер заверша­ющего события.

Рассмотрим оптимизацию комплекса работ по стоимости при нефиксированном сроке выполнения.

Пусть задан сетевой график проекта и известны продол­жительность каждой работы и стоимость ее выполнения в нормальном (D_ij, c_ij) и срочном (d_ij, C_ij) режиме работы. Если все работы выполняются в нормальном режиме, то критичес­кий срок будет наибольшим, а стоимость выполнения — наи­меньшей. Время выполнения проекта может быть уменьше­но путем увеличения стоимости. Необходимо сократить кри­тический срок до некоторого минимально возможного значе­ния при наименьшем возрастании стоимости выполнения проекта.

6.3 Оптимизация проекта по ресурсам. Пусть проект задан сетевым графиком. Для выполнения проекта выделено R единиц ресурса. Каждая работа характе­ризуется продолжительностью выполнения t_ij и интенсив­ностью потребления ресурса r_ij. Под интенсивностью потреб­ления будем понимать требуемое количество ресурса для вы­полнения работы (i, j) в единицу времени. Для простоты до­пустим, что интенсивности постоянные.

Под оптимальным распределением ресурса понимается та­кое размещение работ во времени, при котором в любой момент времени потребность в ресурсах не превышает имеющегося в наличии количества ресурса, а время выполнения проекта ми­нимально.

Источник

Оптимизация сетевой модели по критерию время – число исполнителей

После построения сетевого графика и определения его временных параметров проводят проверку соответствия полученных сроков продолжительности разработки нормативным или директивным срокам. Далее анализируют структуру сетевой модели, выявляя неоднородность напряженности работ проекта.
В настоящее время на практике сетевую модель вначале корректируют по времени, т. е. приводят ее к заданному сроку окончания проекта. Затем приступают к корректировке графика по критерию распределения ресурсов, начиная с трудовых ресурсов.

Минимизация числа исполнителей проекта при сохранении времени его выполнения

• минимизировать количество одновременно занятых исполнителей;
• выровнять потребность в трудовых ресурсах на протяжении всего срока выполнения проекта.

• перемещение работ по оси времени возможно осуществлять только вправо (откладывая их начало);
• работы критического пути трогать нельзя, т. к. это приведет к увеличению срока выполнения всего проекта;
• работы, имеющие свободный резерв времени, можно спокойно перемещать на величину этого резерва;
• перемещение работ, имеющих только полный резерв времени, требует аналогичного сдвига последующих работ;
• передвигаемые работы на линейной диаграмме выделяют, отмечая заметным символом: звездочкой, штрихом, цветом и т.п.

Читайте также:  При значительных объемах трафика уменьшается пропускная способность сети с топологией

Рис. 1. Пример сетевого графика

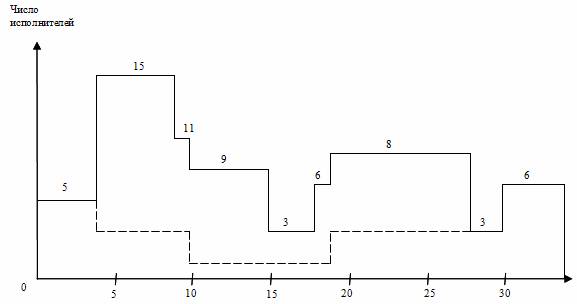
Проведем более детальный анализ линейной диаграммы и карты проекта с целью оптимизации трудовых ресурсов: выравнивая потребность в них на протяжении всего проекта и минимизируя количество одновременно занятых исполнителей. График ежедневной потребности ресурса показывает, что минимальное число исполнителей не может быть меньше 6 человек, что определяется их потребностью для работ критического пути. А 15 исполнителей на участке 5-10 дни проекта является явно завышенным и подлежит коррекции в первую очередь.

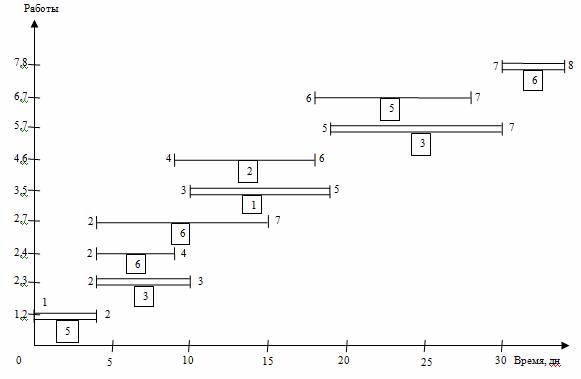
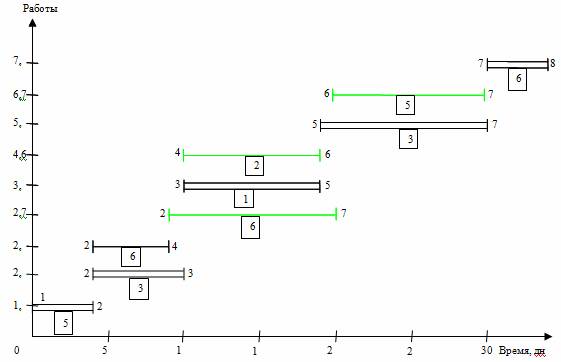
Рис. 2. Линейная диаграмма и карта проекта до оптимизации

15 исполнителей заняты на работах 2,3; 2,4 и 2,7. Работу 2,3 трогать нельзя, т. к. это работа критического пути. Работа 2,4 имеет только полный резерв, но не имеет свободного резерва времени. Работа 2,7 имеет солидный свободный резерв времени и поэтому наиболее предпочтительна для оптимизации. Используем часть свободного резерва, переместив работу 2,7 (5-15 дни) на 5 дней (ее новый срок 10-20 дни). Тем самым максимально необходимое число исполнителей уменьшилось до 9 человек, т.е. задачу минимизации трудовых ресурсов проекта можно принять завершенной.

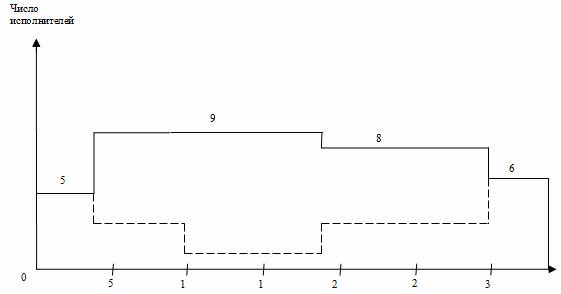
Рис. 3. Линейная диаграмма и карта проекта после оптимизации
Далее решим задачу выравнивания потребности в ресурсах, анализируя интервалы времени, связанные с «провалами» карты проекта. С учетом перемещения работы 2,7 падения спроса на исполнителей в середине проекта (16-18 дни) уже не будет, но он останется ближе к концу проекта (29-30 дни). Чтобы сгладить график загрузки, переместим работу 6,7 (19-28 дни), имеющую свободный резерв времени, на 2 дня (новый срок 21-30 дни). Также для целей выравнивания потребности в трудовых ресурсах переместим работу 4,6 (10-18 дни) на 1 день (11-19 дни).
В итоге оптимизации приходим к линейной диаграмме и карте проекта, представленными на рис. 3. Из графика видно улучшение равномерности загрузки исполнителей: новая ежедневная потребность ресурса составляет от 5 до 9 человек в зависимости от этапа выполнения проекта, резких колебаний занятости нет. Длительность выполнения всего проекта при этом осталась неизменной (34 дня), т. е. необходимое условие оптимизации соблюдено. Видеоинструкция

Источник