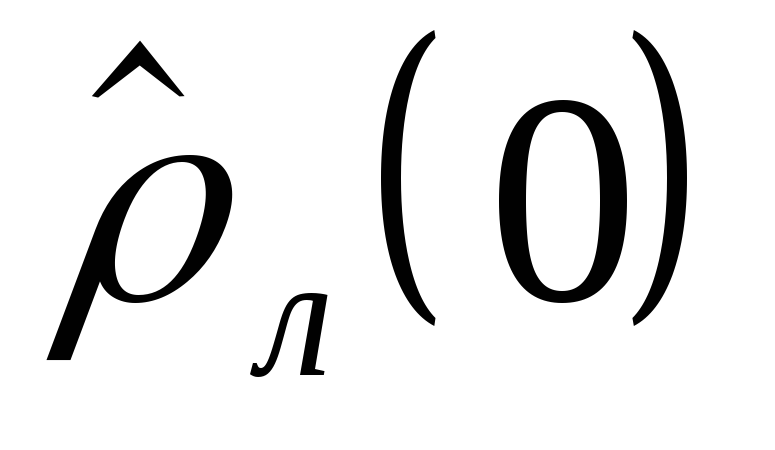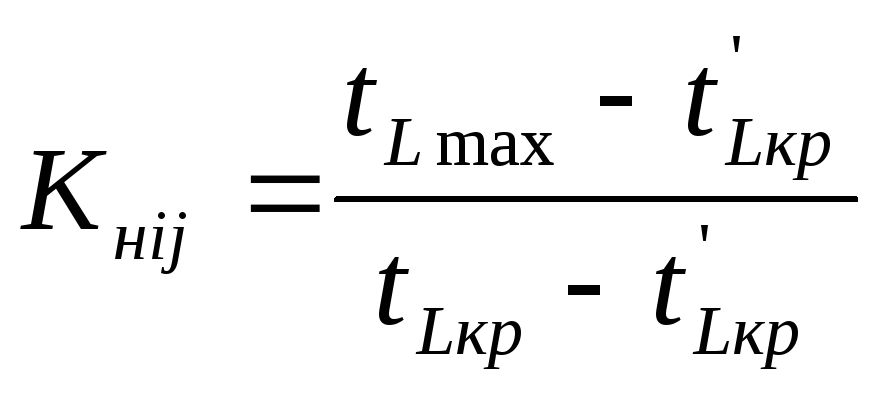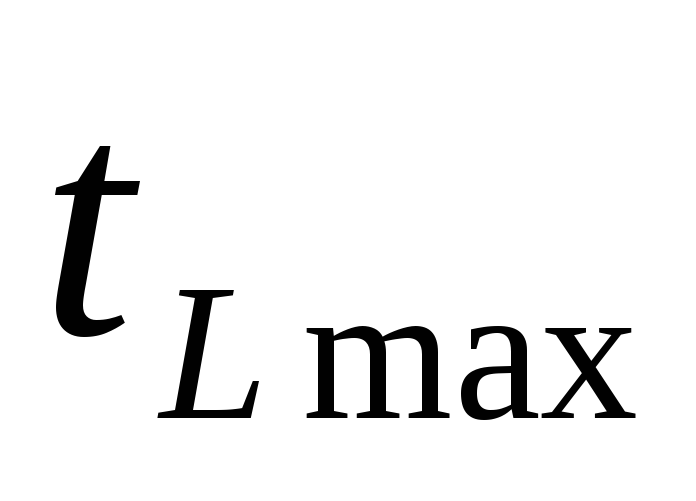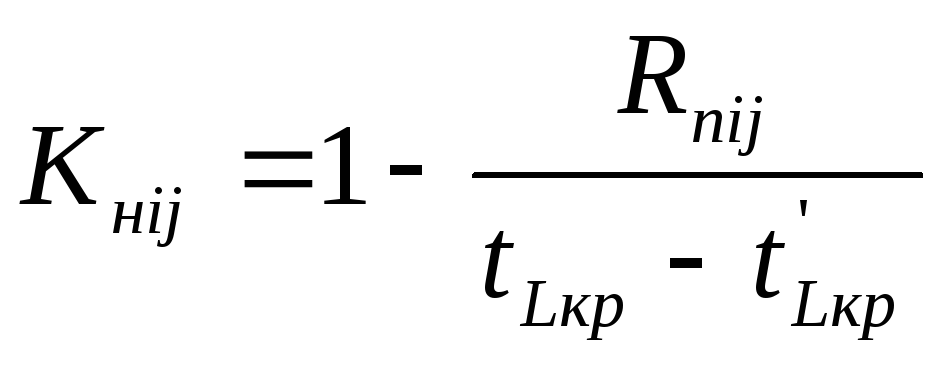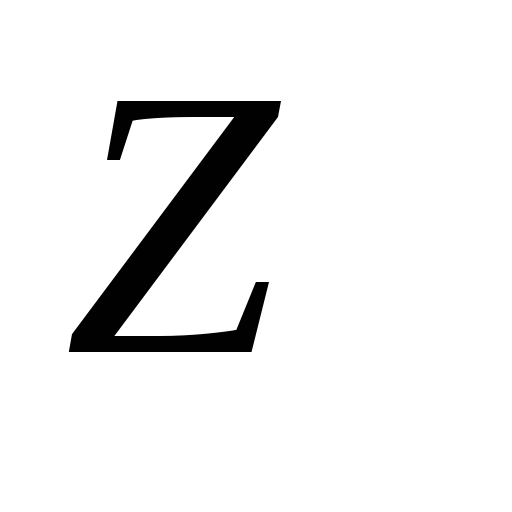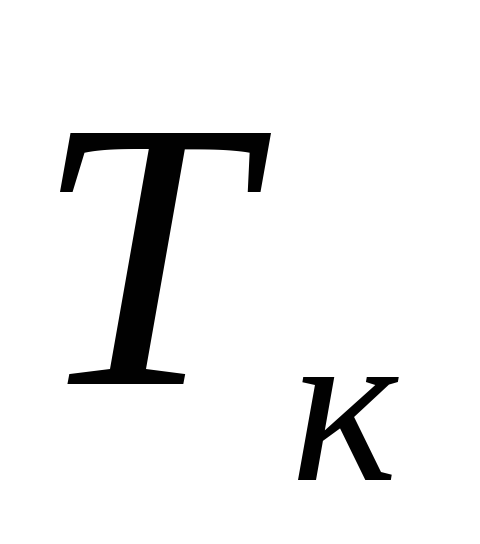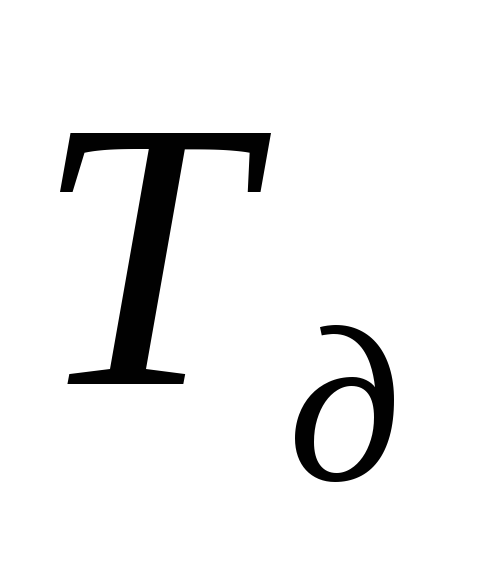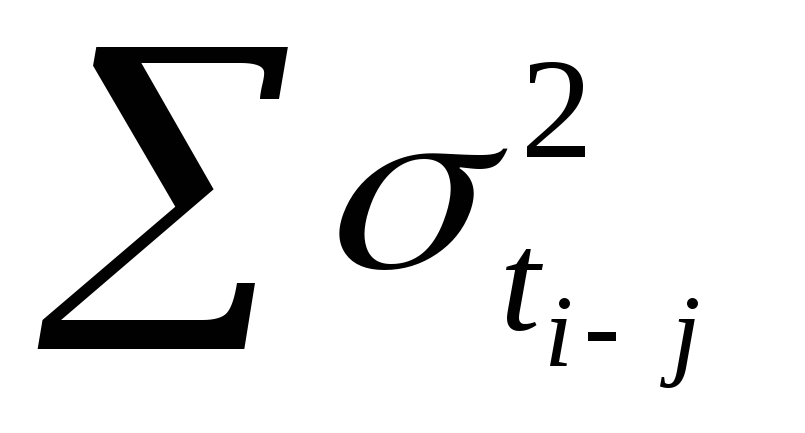Оптимизация сетевых моделей кратко

18. Оптимизация сетевых моделей.

После расчета сетевого графика любым из указанных способов его анализируют с целью установления соответствия полученных сроков продолжительности строительства нормативным или директивным срокам. Корректировку сетевого графика называют оптимизацией графика.

Корректировка графика по продолжительности преследует цель сократить критический путь. Сокращения продолжительности критического пути в результате использования резервов времени, выявленных на некритических работах благодаря привлечению дополнительных ресурсов.

Оптимизация сетевого графика может осуществляться по следующим критериям:

· минимизация времени выполнения комплекса работ при заданных затратах на это выполнение;

· минимизация затрат на выполнение комплекса работ при заданном

Целью оптимизации является сокращение времени выполнения проекта в целом. Эта оптимизация имеет смысл только в том случае, когда длительность выполнения работ может быть уменьшена за счет дополнительных ресурсов, что влечет к повышению затрат на выполнение работ. Для оценки величины дополнительных затрат, связанных с ускорением выполнения той или иной работы, используются либо нормативы, либо данные о выполнении аналогичных работ в прошлом.

Исходными данными для проведения оптимизации являются:

· нормальная длительность работы;

· затраты на выполнение работы в нормальный срок;

· затраты на выполнение работы в ускоренный срок.

Оптимизацию можно проводить двумя способами.

Первый способ заключается в уменьшении продолжительности выполнения работ, осуществляемых в нормальном режиме, начиная с тех, которые дают наименьший прирост затрат.

Второй способ заключается в увеличении продолжительности выполнения работ, осуществляемых в ускоренном режиме, начиная с тех, которые дают наибольший прирост затрат.

19. Метод вероятностного моделирования.

Прогнозирование с использованием вероятностных моделей базируются на методе экспоненциального сглаживания. Вероятностные модели по своей сути отличны от экстраполяционных моделей временных рядов, в которых основой является описанные изменения во времени, процесса.

Во временных рядах модели представляют собой некоторую функцию времени с коэффициентами, значения которых оцениваются по наблюдениям. В вероятностных моделях оцениваются вероятности, а не коэффициенты.

Пусть мы имеем n взаимно независимых и исключающих событий. В каждом случае наблюдения измеряются в единой шкале, помещаются в (n+1) ограниченный класс и обозначаются так: . Событие связанное с наблюдением Х (t), соответствует числу интервалов в которое это событие попадает, т.е. существует единственное значение К, такое, что Х. И поэтому К-е событие связывается с наблюдением X(t).

Рассмотрим метод оценивания вероятностей , связанных с различными событиями Х

На первом этапе задаются начальные значения различных вероятностей: :

К = 1,2. n. Наблюдение Х(t) связано с К-м событием следующим образом: если Х то строится единый вектор компонент который равен 0 и К-й компонент равен 1. Это может быть К-м столбцом единичной матрицы ранга К.

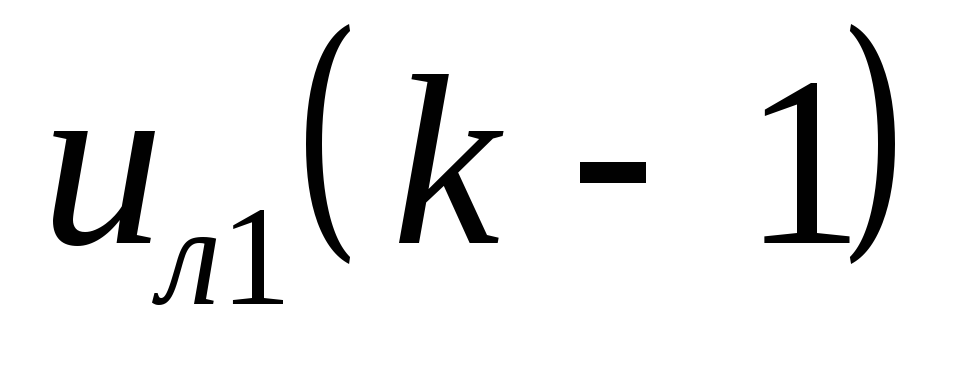
Предположим, что имеются пять классов и наблюдение попало во второй класс, соответствующий единичный вектор будет

Процесс реализующий оценки вероятностей, описывается вектором сглаживания по формуле:

Каждая компонента вектора меняется по закону экспоненциального сглаживания между 0 и 1. Если вероятностный, то все его компоненты должны быть неотрицательными и их сумма должна быть равна 1. Значение оценки есть результат экспоненциального сглаживания, и если распределение вероятностей наблюдений X (t) не меняется, то полученные вероятности и будут действительными вероятностями К-го события.

Значения компонент вектора представляют собой выборку с биноминальным распределением, поэтому дисперсия К-й компоненты будет . Дисперсия оценок К-й вероятности определяется соотношением 

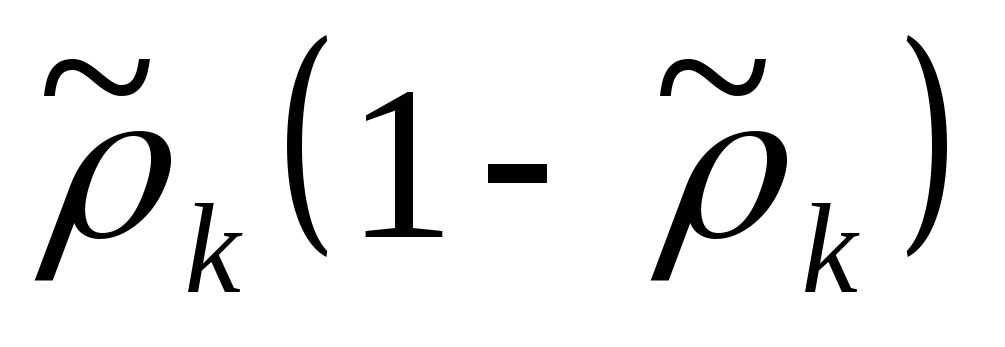
где  — константа сглаживания (01) используемая для получения оценок вектора вероятностей.

Возможны два варианта: в первом варианте пределы классов заданы так, что может быть или очень большим (около 1) или очень маленьким (около 0). Тогда дисперсия компонент вектора вероятностей будет небольшой. Если форма распределения меняется со временем, большое значение компонента сглаживания может быть использована, чтобы устранить влияние “старой” информации.

Во втором варианте распределение вероятностей постоянно во времени и нет необходимости “взвешивать” старую информацию. Малое значение компоненты сглаживания, может использовать меньшие интервалы классов с не очень большими вероятностями. Вероятностная модель оперирует последовательностью наблюдений с учетом их распределения и игнорирует последовательность этой информации уже непосредственно во времени. Поэтому вектор вероятностей , который служит текущей оценкой вероятностей n отдельных событий, является оценкой этих вероятностей в будущем. Последовательность наблюдений может быть представлена как временной ряд х(t), где x измерен по некоторой шкале есть min и max возможных значений наблюдений.

Пусть x случайная величина с ожиданием m и конечной дисперсией . Тогда сумма n случайных выборок будет нормально распределена со средним nm и дисперсией и вероятности как сумма точек наблюдений будут распределены нормально.

Пусть случайная величина Х распределенная между нулем и единицей. Введем функцию f(x) =

если Yn — сумма N случайных выборок, тогда функция распределения этих сумм будет

где 0yN. Находим среднее значение и дисперсию для величины y.

Yp является точкой распределения и ее можно выразить через среднюю и дисперсную распределения

, где Kp — некоторый множитель, учитывающий число степеней свободы распределения.

Данное управление может служить основой оценок для вероятностной модели. При достаточном количестве исходной информации вероятностная модель может дать вполне надежный прогноз. Недостатком является требование достаточно большого количества наблюдений и назначение начального распределения, что может привести к неправильным оценкам.

Экстраполяция базируется на допущениях: 1) развитие явления может быть с достаточным основанием охарактеризовано плановой траекторией-трендом; 2) общие условия, определяющие тенденцию развития в прошлом, не претерпят существенных изменений в будущем. Недостатки данного метода: 1) он исходит из прошлого и настоящего и поэтому накапливаются погрешности; 2) необходимый выбор периода упреждения прогноза. Положительные рез-ты метод дает на 1-2 года, дальше будут ошибки; 3) практическая невозможность получения статистическими методами кривой требуемой формы. Поэтому, чтобы предупредить ошибки в прогнозе, метод экстраполяции следует сочетать с другими методами прогнозирования.

Метод экстраполяции применяется при стабильности системы, устойчивости явлений, когда динамика процессов, показателей в перспективе опред-ся тенденциями их изменения в прошедшем периоде. Предполагается, что развитие идет непрерывно, гладко, силы прошлого в состоянии контролировать будущее. Прогноз становится проекцией прошлого в будущее.

Источник

5.Анализ и оптимизация сетевых моделей.

С учетом рассчитанных параметров необходимо оценить целесообразность структуры сетевого графика, внести возможные изменения. Пересоставление графика может сводиться к устранению лишних работ, более целесообразному расчленению работ, установления параллельности выполнения работ.

Анализ сетевого графика предусматривает расчет коэффициентов напряженности работ К_нij:

(3.17)

где — продолжительность максимального пути, проходящего через данную работу;

— продолжительность отрезка пути , совпадающего с критическим путем.

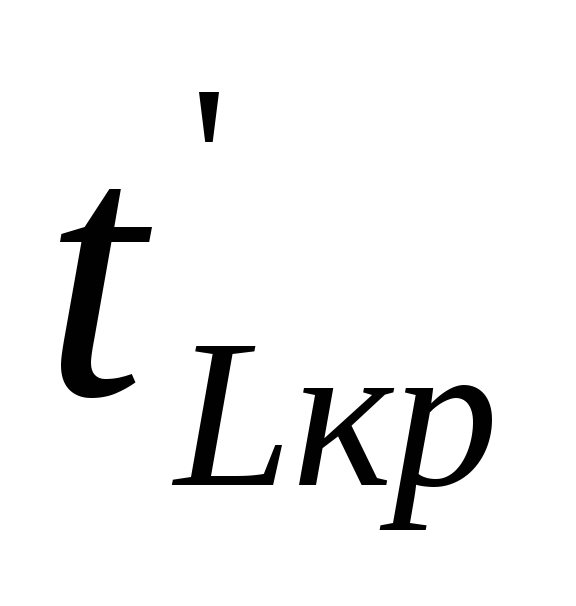
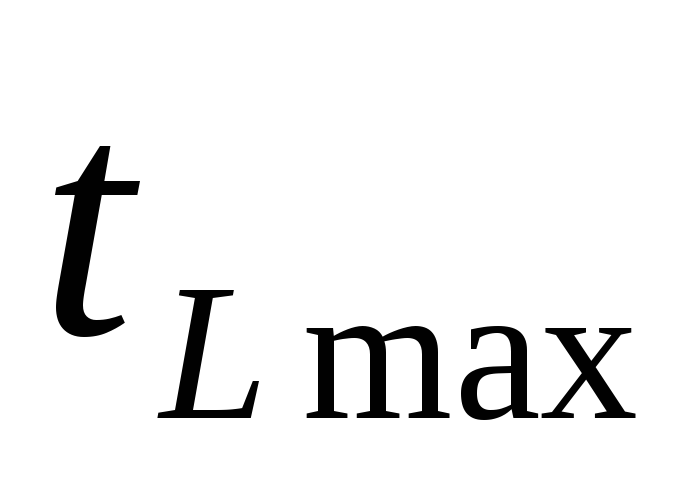
(3.18)

Рассчитанные коэффициенты следует внести в последнюю графу табл. 3.4.

Расчет позволяет распределить все работы по зонам (критическая, подкритическая, резервная).

Следующей задачей анализа является определение вероятности свершения завершающего события в заданный срок (Р_к).

(3.19)

где -аргумент функции нормального распределения вероятностей;

— срок свершения завершающего события по расчету (t ) в днях;

— заданный (директивный) срок свершения завершающего события, дн.;

— сумма дисперсии работ, лежащих на критическом пути.

При Р_к  0,35 опасность нарушения заданного срока свершения завершающего события настолько велика, что необходимо повторное планирование с перераспределением ресурсов. В этом случае необходима оптимизация сетевого графика по времени. Она проводится путем переброски ресурсов с ненапряженных путей на критический, что приводит к сокращению его продолжительности.

При Р_к  0,65 можно считать, что на работах критического пути имеются избыточные ресурсы и, следовательно, общая продолжительность работ может быть сокращена.

Таблица 12.5 – таблица значений функции нормального распределения вероятностей

Оптимизация сетевого графика может быть направлена на решение различных задач, в частности:

а) сокращение критического пути до директивного срока выполнения комплекса работ;

б) минимизация численности исполнителей.

в) минимизация затрат при заданном времени. Наиболее широко используется первое направление.

Методы оптимизации также могут быть различными. В процессе оптимизации необходимо ориентироваться на коэффициенты напряженности работ, виды ресурсов, необходимых для выполнения работ (квалификация работников, виды оборудования, источники финансирования и др.), величины резервов работ и их виды (полный, частный, свободный).

Оптимизация с целью сокращения критического пути может быть выполнена с помощью графика

0,72 ТК СТ Т

0 1 4 6 11 13

0,86 Т Т К СТ Т

1Т Т К СТ СБ Т х х

Условные обозначения: Т – технологи;

Работы располагаются: а) слева направо в последовательности их выполнения (начальных и конечных событий, которые обозначаются шифрами) в определенном масштабе;

б) снизу вверх в порядке убывания коэффициентов напряженности без соблюдения масштаба.

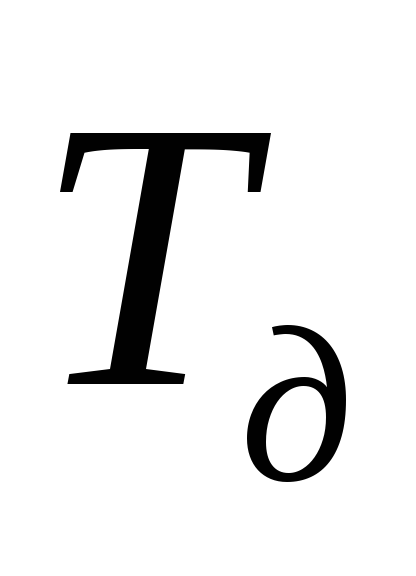
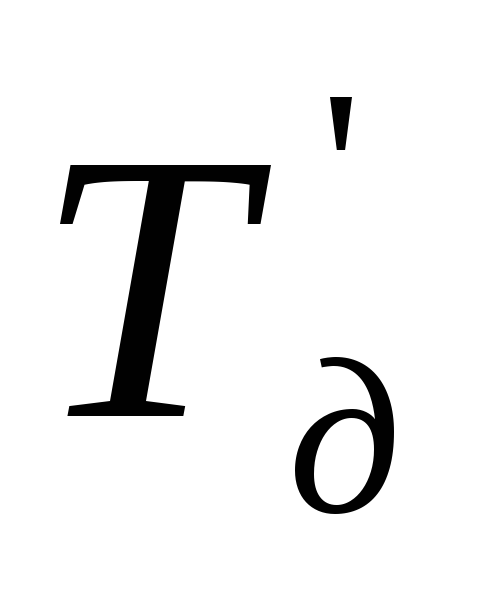
На критическом пути или прямой, представляющей его продолжение, наносится точка, или директивный срок выполнения комплекса работ.

С помощью условных обозначений (цвета, букв, шифров) на графике наносится вид ресурсов каждой работы или только работ, имеющих аналогичные ресурсы.

С ненапряженных работ ресурсы перераспределяются на работы критического и подкритического путей. При изъятии ресурсов с какой-либо работы рассчитывается время ее удлинения. Оно сравнивается с величинами резервов этой работы с учетом их вида и использования на других работах данного пути. Увеличение времени работы должно быть меньше ее полного резерва или части полного резерва времени работы, оставшейся после изъятия ресурсов других работ данного пути.

Оптимизация сетевого графика при ограниченных ресурсах требует составления линейной диаграммы и графика ежедневной потребности ресурсов.

После перегруппировки ресурсов возможно изменение топологии сетевого графика. Тогда производится перешифровка работ, и измененные шифры вносятся в перечень работ (таблица 12.1). Затем следует пересчет параметров сетевого графика, анализ с определением коэффициентов напряженности и дальнейшая оптимизация, если она возможна.

После первой оптимизации следует определить, насколько сократился критический путь и исчерпаны ли возможности оптимизации.

Если в результате оптимизации критический путь станет равен директивному сроку или меньше его, то можно оставить полученный вариант графика. Если же критический путь остается больше директивного срока, то необходимо рассчитать потребность в дополнительных ресурсах для сокращения критического пути на величину равную Т_д — t_lkp

Источник