Понятие о сетевых моделях и правила построения сетевых графиков
Сетевая модель отражает комплекс работ и событий проекта в их логической и технологической последовательности. Анализ сетевой модели позволяет выявить взаимосвязи этапов проекта и определить оптимальный порядок их выполнения, например, для сокращения сроков реализации проекта.
Математический аппарат сетевых моделей базируется на теории графов. Графом называется множество точек (вершин), определенные пары которых соединены отрезками. Отрезки называются дугами, если указано, какая из двух вершин является начальной, или ребрами, если ориентация не указана. Граф, состоящий из дуг, называется ориентированным (орграфом), образованный ребрами — неориентированным.
Пример ориентированного графа (орграфа)
Пример неориентированного графа
Последовательность дуг или ребер, ведущая от некоторой вершины к другой, образует путь.
Сетевая модель представляется сетевым графиком, определяющим логическую взаимосвязь работ (понятия сетевой модели и сетевого графика используются часто как синонимы).
Сетевые графики представляют собой ориентированные графы, дугам или вершинам которых приписаны некоторые числовые значения.
Вершины или события соответствуют моментам начала или окончания одной или нескольких операций, а дуги – операциям.
Различают три вида событий: исходное, завершающее и промежуточное. С исходного события начинается выполнение проекта. Завершающее событие соответствует достижению конечной цели, т. е. завершению комплекса операций. Сетевые графики с несколькими завершающими событиями называются многоцелевыми. К промежуточным относятся все прочие события.
Моментом свершения события считается момент окончания выполнения всех входящих в это событие операций. До этого момента не может быть начата ни одна из непосредственно следующих за событием операций.
Различают три вида операций:
1) действительная операция () требует затрат времени и ресурсов (разработка проекта, подвоз материалов, выполнение монтажных работ);
2) операция — ожидание () требует только затрат времени (затвердение бетона, сушка штукатурки перед началом малярных работ, рост растений и т. д.);
3) фиктивная операция () — технологическая или ресурсная зависимость в выполнении некоторых операций.
При построении сетевых графиков соблюдается ряд правил:
1) в сети не должно быть событий (кроме исходного), в которые не входит ни одна дуга;
2) не должно быть событий (кроме завершающего), из которых не выходит ни одной дуги;
3) сеть не должна содержать замкнутых контуров (циклов);
4) любая пара событий сетевого графика может быть соединена не более чем одной дугой. Например, для трех одновременно выполняемых операций , , на Рис. 15.1. возникает путаница из-за того, что они имеют одинаковое обозначение (3,6). В этом случае вводятся дополнительные события и новые фиктивные операции;
5) номер начального события любой операции должен быть меньше номера ее конечного события.
Построение сетевого графика начинается с составления списка необходимых операций. Их продолжительность устанавливается на основе нормативов или по аналогии с ранее выполнявшимися операциями. Такие временные оценки называются детерминированными. При отсутствии нормативов определяются вероятностные временные оценки. После составления списка операций приступают к построению графика.
Рассмотрим проект, представленный с помощью следующей таблицы:
Таблица 1. Описание составных работ проекта
| Работа | Непосредственно предшествующие работы | Время выполнения |
| A | — | |
| B | — | |
| C | B | |
| D | A, C | |
| E | C | |
| F | C | |
| G | D, E, F |
Анализ последовательности и взаимозависимости работ, приведенных в таблице, позволяет построить сетевой график (Рис. 2).
Рис. 15.2. Сетевой график рассматриваемого проекта.
Здесь использованы две фиктивные работы (3,4) и (5,6). Они не требуют затрат времени и используются лишь для того, чтобы правильно отобразить взаимосвязь между работами.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
1. Элементы построения сетевых моделей
В основе метода сетевого планирования и управления (СПУ) лежит построение графика, по своему виду напоминающего сеть (переплетение нитей и узелков), поэтому график и получил название сетевого.
Сетевой моделью называется отображение процессов, выполнение которых подчинено достижению одной или нескольких целей, с указанием взаимосвязей между этими процессами.
Сетевым графиком называется график производства работ с установленными расчётом сроками их выполнения. Сетевой график представляет собой графическое изображение сетевой модели с рассчитанными параметрами.
Элементами сетевой модели являются работа, событие и путь:
а) работа – это трудовой процесс, требующий затрат времени и ресурсов.
Название работы является минимальной информацией о работе, содержащейся в сетевой модели (например, отрывка котлована, возведение каркаса, устройство кровли, поставка оборудования и т.д.).
Работа на графике изображается сплошной стрелкой, направленной слева направо с указанием над стрелкой продолжительности работы.
Работа, которая требует лишь затрат времени, называется работа – ожидание. Ожидание на графике изображается пунктирной стрелкой с указанием над стрелкой её продолжительности (например, процесс твердения бетона или ожидание поставки материалов). Эти работы требуют только затрат времени.
Для отображения правильной технологической последовательности между работами применяется зависимость. Ни времени, ни ресурсов «зависимость» не требует. На графике зависимость изображают пунктирной стрелкой, продолжительность которой равна нулю. В литературных источниках зависимость называют фиктивной работой.
Итак, понятие «работа» может иметь три значения:
работа
работа – ожидание
зависимость
б) событие – это итог какой-нибудь деятельности (работы), происходящей мгновенно. Любая работа начинается и заканчивается событием.
Событие не потребляет ни времени, ни трудовых ресурсов, оно обозначает только факт начала и окончания одной или нескольких работ. Событие графически обозначается кружком, внутри которого ставится его номер, или может обозначаться буквами.
Событие, не имеющее непосредственно предшествующих работ, называется исходным, не имеющее непосредственно следующих работ – завершающим. Событие, не являющееся ни исходным, ни завершающим, называется промежуточным.
На рис. 1 событие 1 – исходное, событие 6 – завершающее, события 2, 3, 4, 5 – промежуточные.
Все работы комплекса по отношению друг к другу подразделяются на данную, предшест-вующую и последующую работы. Обозначение работ см. на рис. 2.
в) путь – это непрерывная технологическая последовательность работ от исходного события к завершающему.
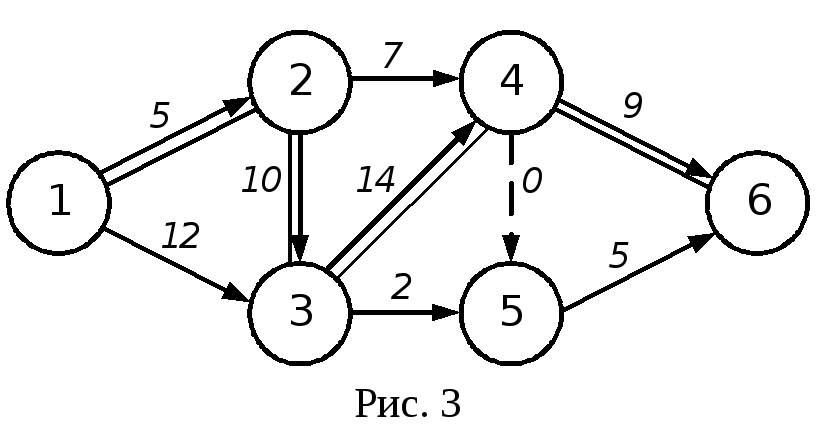
На рис. 3 дан сетевой график из восьми работ, одной зависимости и шести событий. На графике можно выделить 7 путей:
1-й путь проходит по событиям 1, 2, 3, 4, 6;
2-й путь проходит по событиям 1, 3, 5, 6;
3-й путь проходит по событиям 1, 2, 4, 6;
4-й путь проходит по событиям 1, 2, 3, 5, 6;
5-й путь проходит по событиям 1, 2, 3, 4, 5, 6;
6-й путь проходит по событиям 1, 2, 4, 5, 6;
7-й путь проходит по событиям 1, 3, 4, 5, 6.
Зная продолжительность каждой работы tij , можно определить продолжительность любого пути сетевого графика.
Продолжительность пути определяется как сумма продолжительностей работ, составляющих этот путь:
Критический путь – это путь, имеющий максимальную продолжительность. Он определяет конечный срок строительства, это самый трудоемкий и неблагоприятный путь.
Подкритический путь – это путь, продолжительность которого близка к продолжительности критического пути.
На рис. 3 длина различных путей от исходного события до завершающего равна:
1-й путь Т1 = 5 + 10 + 14 + 9 = 38;
4-й путь Т4 = 5 + 10 + 2 + 3 = 20;
5-й путь Т5 = 5 + 10 + 0 + 3 = 32;
6-й путь Т6 = 5 + 7 + 0 + 3 = 15;
7-й путь Т7 = 12 + 14 + 0 + 3 = 29.
Первый путь имеет наибольшую продолжительность из всех путей, значит, он является критическим.
Критическим путь назван потому, что, во-первых, из всех путей сетевого графика только он определяет общую продолжительность строительства; во-вторых, он указывает на работы, которые являются ведущими для выполнения заданного комплекса работ. Работы, лежащие на критическом пути, называются критическими.
На рис. 3 критическими работами являются 1-2; 2-3; 3-4; 4-6.
На сетевом графике критический путь выделяют красной двойной или жирной линией.
В сетевом графике может быть несколько критических путей одинаковой продолжительности. Определение продолжительности (длины) критического пути и критических работ – одна из основных задач, решаемых в методе сетевого планирования и управления (СПУ).
1.2 Основные понятия сетевого планирования
Следует выделить следующие понятия, необходимые для сетевого планирования.
Работа – производственный процесс, требующий затрат времени и материальных ресурсов и приводящий к достижению определенных результатов.
По своей физической природе работы можно рассматривать как действие (например, заливка фундамента бетоном, составление заявки на материалы, изучение конъюнктуры рынка), процесс (пример — старение отливок, выдерживание вина, травление плат) и ожидание (процесс, требующий только затраты времени и не потребляющий никаких ресурсов; является технологическим (твердение цементной стяжки) или организационным (ожидание сухой погоды) перерывом между работами, непосредственно выполняемым друг за другом.
По количеству затрачиваемого времени работа может быть:
- действительной, то есть протяжённым во времени процессом, требующим затрат ресурсов;
- фиктивной (или зависимостью), не требующей затрат времени и представляющей связь между какими-либо работами: передача измененных чертежей от конструкторов к технологам, сдача отчета о технико-экономических показателях работы цеха вышестоящему подразделению.
1.3 Правила построения сетевых моделей
- какие работы должны быть завершены до начала данной работы;
- какие работы должны быть начаты после завершения данной работы;
- какие работы необходимо выполнять одновременно с выполнением данной работы.