Основные расчеты сетевой модели

1.3. Методы расчета параметров сетевой модели

Для расчета параметров сетевых моделей применяют следую­щие три метода:

• метод вычислений непосредственно на сетевом графике;
• матричный метод,
• табличный метод.

Все эти методы основываются на формулах (1.6), … (1.10) и от­личаются только процедурами вычислений.

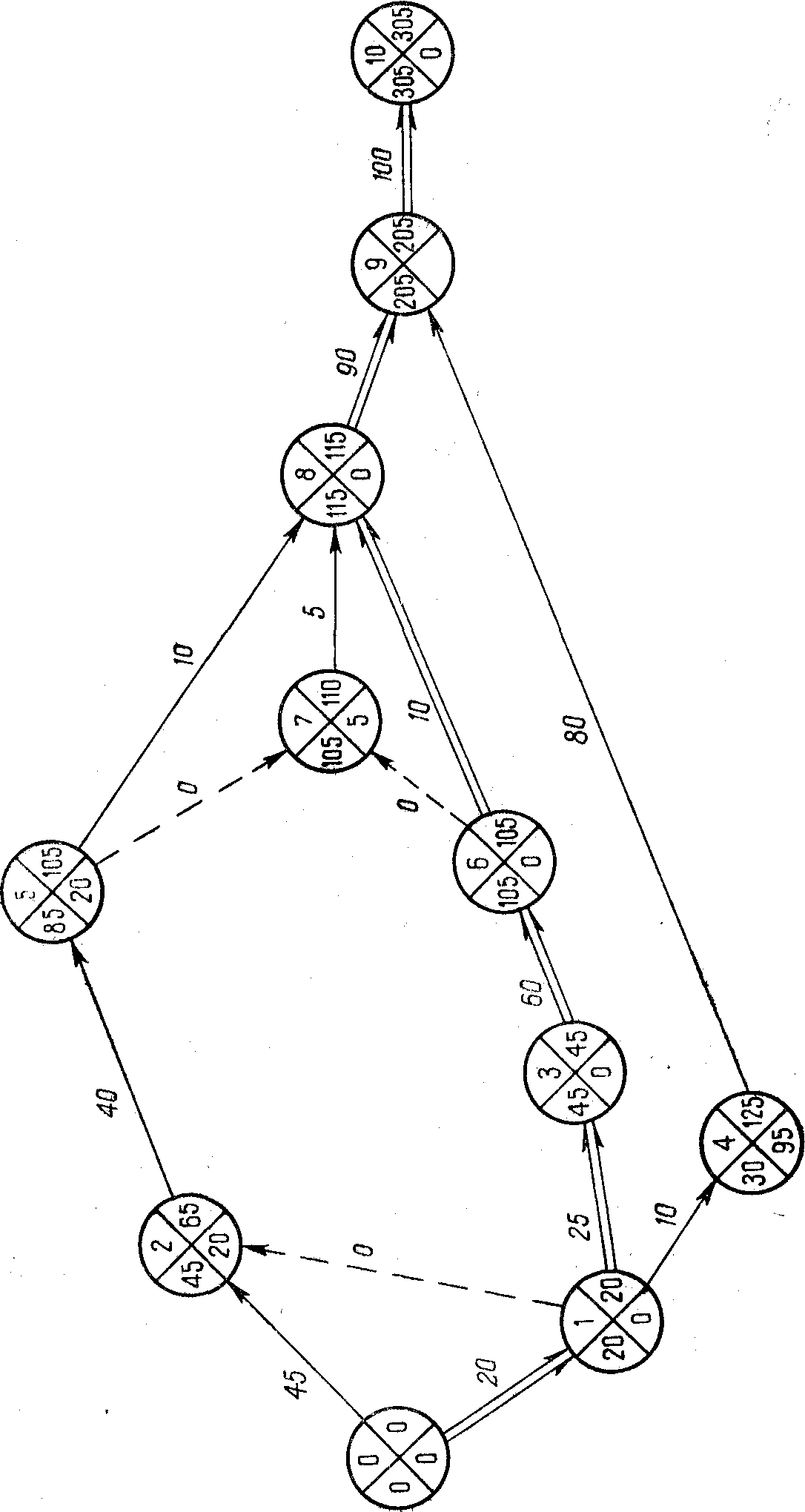
Метод вычислений на сетевом графике. Предварительно каж­дый кружок, изображающий вершину графика (событие), делится на четыре сектора: в верхний сектор записывается номер собы­тия k, в левый – значение Т_k (p) , в правый – T_k (n) , а в нижний – R_k = T_k (n) –Т_k (p) (рис. 1.4).

Согласно формуле (1.6) ранний срок наступления данного со­бытия определяется как сумма раннего срока непосредственно предшествующего события и длины дуги (продолжительности ра­боты), которая их соединяет. Если к событию подходят две или большее число дуг, то вычисляют указанные суммы для каждой из входящих дуг; максимальная из сумм и есть ранний срок на­ступления данного события, который записывается в левый сектор. Расчет ведется последовательно от исходящего события к завер­шающему.

Обратимся к рис. 1.4, на котором изображена та же сетевая мо­дель, что и на рис. 1.3. В левый сектор исходящего события сразу записывается значение T₀ (p) = 0. Далее находим: к событию 1 под­ходит одна дуга (0, 1), поэтому T₁ (p) = 0+20 = 20; к событию 2 под­ходят две дуги (0, 2) и (1, 2), поэтому T₂ (p) = max=45, и так далее Каждое вычисленное значение T_k (p) сразу записывает­ся в соответствующий сектор.

Поздний срок наступления данного события согласно формуле (2.10) определяется как разность между поздним сроком непосред­ственно следующего события и длиной дуги, которая их соединяет. Если из события выходят две или большее число дуг, вычисляют указанные разности для каждой из выходящих дуг; минимальная из разностей и есть поздний срок наступления данного события, который записывается в правый сектор.

Поздний срок наступления завершающего события согласно формуле (1.9) равен раннему сроку, эту величину записывают в правый сектор и далее ведут расчет последовательно от завершаю­щего события к исходящему.

Для нашего сетевого графика имеем T₁₀ (n) = T₁₀ (p) =305. Далее находим: из событий 9, 8, 7 выходит по одной дуге, поэтому T₉ (n) = 305–100 =205; T₈ (n) =205–90=115; T₇ (n) =115–5=110;

из со­бытия 6 выходят две дуги (6, 7) и (6, 8), поэтому T₆ (n) = min =105 и так далее.

После того, как рассчитаны все значения T_k (n) вычисляют ре­зервы времени событий как разности между величинами, записан­ными в левых и правых секторах, и записывают их в нижние сек­торы. Остальные параметры сетевой модели вычисляют, по форму­лам (1.11)–(1.17). Результаты всех расчетов удобно представить в виде табл. 1.2.

Критический путь проходит через события, для которых R_j=0 (0–3–6–8–9–10).

При расчете параметров сетевой модели непосредственно на графике можно не нумеровать события так, чтобы выполнялось условие ij для любой дуги (i, j).

Матричный метод. Метод сводится к простым формальным опе­рациям над величинами t_ij без необходимости обращаться к гра­фику. Процедуру расчета рассмотрим на примере сетевой модели, изображенной на рис. 1.3.

Представим сетевой график в виде матрицы смежности, но вместо единиц запишем соответствующие значения t_ij. В результате получим табл. 1.3 (в таблицу также записаны величины T_i (p) и T_j (n) , которые еще нужно вычислить).

Таблица может быть составлена как по сетевому графику, так и по упорядоченному перечню событий и работ.

Правило определения раннего срока событий вытекает из вы­ражения (1.6) и формулируется следующим образом: ранний срок события с номером j, равен сумме элемента матрицы t_ij с ранним сроком предшествующего события, причем, если предшест­вующих событий несколько, то берется максимальная из сумм, ре­зультат записывается в строку с номером i=j.

Так как ранний срок нулевого события равен нули, то сразу записывают в нулевую строку значение T₀ (p) =0. Дальше последо­вательно просматриваются столбцы (последующие события), начи­ная с первого (j=1). Из матрицы видим, что событие 1 связано только с одним предшествующим событием, а именно – с нулевым, причем t_0,1=20. Складываем t_0,1 со значением Т₀ (p) = 0, записан­ным в столбце Т_i (p) по нулевой строке, а результат t_0,1+T₀ (p) = 20 записываем в первую строку в столбец Т_i (p) . Это и будет значе­ние T₁ (p) .

Переходим ко второму столбцу (j=2). Событие 2 связано с двумя предшествующими событиями: 0 и 1, причем t_0,2=45; t_1,2=0. Составляем две суммы t_0,2+ Т₀ (p) = 45+0=45; t_1,2+T₁ (p) = 0+20 = 20 и большую записываем во вторую строку в стол­бец Т_i (p) .

Рассмотрим еще восьмой столбец (j=8). Событие 8 связано с тремя предшествующими событиями 5, 6 и 7. Составляем суммы 10+85=95; 10+105=115; 5+105=110 и в восьмую строку в стол­бец Т_i (p) записываем наибольшую, равную 115.

Правило вычисления позднего срока события следует из выра­жения (2.10) и формулируется следующим образом: поздний срок события с номером i, определяется путем вычитания элемента матрицы t_ij из позднего срока последующего события, причем, если последующих событий несколько, то берется мини­мальная из разностей; результат записывается в столбец с номе­ром j=i.

Вычисления начинают с завершающего события и сразу запи­сывают в столбец для j=N величину T_N (n) = Т_N (p) . В нашем случае в столбец для j=10 записывают Т₁₀ (n) =305. Теперь просматриваем последовательно строки, начиная с N–1 (в нашем случае девя­той). Из таблицы видно, что событие 9 связано с одним последую­щим событием 10, причем t_9,10=100. Вычитаем согласно правилу из T₁₀ (n) =305 величину t_9,10=100 и разность, равную 205, записы­ваем в девятый столбец в строку Т_j (n) . Это и будет величина T_9(n)=205.

Переходим к следующей, восьмой строке (i=8). Событие 8, как видно из матрицы, связано с одним последующим событием 9, причем t_8,9=90. Составим разность 205–90=115 и результат за­пишем в восьмой столбец в строку T_j (n) .

Рассмотрим пятую строку. Событие 5 связано с двумя после­дующими событиями 7 и 8, а соответствующие элементы матрицы t_5,7=0 и t_5,8=10. Составляем две разности 110–0=110; 115–10=105 и меньшую из них за­пишем в пятый столбец в строку T_j (n) . Это и будет T₅ (n) =105

Остальные параметры вычисляют по формулам (1.11) – (1.17), записывают их в табл. 1.2 и определяют критический путь.

Табличный метод в принципе не отличается от изложенных ме­тодов и преимуществ перед ними не имеет.

Теперь обратимся к сетевым моделям, у которых продолжи­тельности работ являются случайными величинами. В этом случае продолжительность критического пути также является случайной величиной; сохраним за ней обозначение Т_кр. Исходная инфор­мация таких моделей содержит сеть, законы распределения веро­ятностей величин t_ij (или вероятностные оценки a_ij, b_ij, m_ij) и (но не обязательно) директивный срок наступления завершающего события Т_дир.

Основными задачами анализа этих моделей являются:

– определение среднего значения и дисперсии критического времени T_кр;

– определение закона распределения величины T_кр;

– определение таких сроков наступления событий, которые с заданной вероятностью не будут превышены;

– определение законов распределения для моментов наступле­ния событий;

– определение вероятности прохождения критического пути через данную работу или совокупность работ.

Существующие аналитические методы решения перечисленных задач весьма громоздки и не нашли практического применения. Более широкое применение получил метод статистических испы­таний.

Далее излагается практически удобный для расчетов метод ве­роятностной оценки наступления завершающего события. Необхо­димо подчеркнуть, что вероятностный анализ для завершающего события особенно важен, поскольку для продолжительности вы­полнения комплекса, как правило, устанавливается директивный срок и характер распределения случайного реального завершения комплекса работ по отношению к директивному сроку может суще­ственно влиять на принятые решения при управлении выполнением комплекса.

Рассмотрим следующие задачи вероятностного анализа сверше­ния завершающего события:

– определить вероятность того, что продолжительность крити­ческого пути (выполнения комплекса работ) T_кр лежит в задан­ных пределах

– определить вероятность того, что продолжительность крити­ческого пути не превысит заданный директивный срок;

– определить такой директивный срок, который с заданной ве­роятностью не будет превышен.

В методе приняты некоторые допущения, из которых выделим два основных:

1. Дисперсия D_кр величины критического времени зависит толь­ко от дисперсий работ, лежащих на критическом пути.

2. Величина T_кр распределена по нормальному закону. Это допущение основывается на предположении, что число работ крити­ческого пути достаточно велико и что продолжительности этих работ являются независимыми случайными величинами. Согласно центральной предельной теореме сумма достаточно большого числа независимых случайных величин, сравнимых по дисперсии, при­ближенно распределена по нормальному закону.

Расчет для всех задач начинается с вычисления математических ожиданий продолжительностей t_ij для всех работ комплекса по формуле (1.1) или (1.3). Затем, оперируя величинами как детерминированными:

– вычисляют продолжительность критического пути , представляющую собой математическое ожидание случайной величины T_кр;

– определяют критический путь L_кр;

– вычисляют дисперсии D_ij продолжительностей работ, лежащих на критическом пути, по формуле (1.2) или (1.4);

– на основании известной теоремы, что дисперсия суммы независимых величин равна сумме дисперсий слагаемых, находят дисперсию продолжительности критического пути

Теперь при сделанных допущениях можно решить первую из перечисленных выше задач, а именно – определить вероятность того, что продолжительность критического пути лежит в заданных пределах : |

t – аргумент функции Лапласа ;

– математическое ожидание случайной величины Т_кр;

Перейдем ко второй задаче. Согласно принятому допущению случайная величина Т_кр распределена по нормальному закону, по­этому на основании правила трех сигм можно написать

Очевидно, что директивный срок должен лежать в тех же пре­делах:

Действительно, если то вероятность выпол­нения комплекса работ равна нулю; если же взять то без оснований будет растянут срок выполнения комп­лекса.

Кроме того, должно выполняться условие

Из неравенств (1.20), (1.21), (1.22) следует, что

Теперь можно найти решение второй задачи – определить ве­роятность того, что продолжительность критического пути не пре­высит заданный директивный срок. Искомую вероятность получим из выражения

Третью задачу можно решить следующим образом. С учетом заданной вероятности Р₃ перепишем выражение (1.24) в виде

По известным величинам Р₃, и _кр можно определить с помощью таблиц функции Лапласа величину Т_дир, удовлетворяю­щую уравнению (1.25).

Недостаток метода состоит в том, что анализ проводится лишь для одного критического пути. Но при случайных длительностях t_ij совокупность работ, составляющих критический путь, также является случайной и может не совпадать с совокупностью работ анализируемого критического пути. Возможность таких несовпаде­ний возрастает, если имеются полные пути, продолжительность ко­торых незначительно отличается от продолжительности критиче­ского пути. Поэтому для принятия эффективных решений необхо­димо иметь надежные вероятностные оценки длительности работ комплекса.

Источник