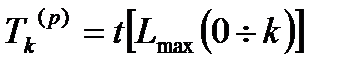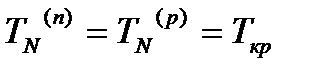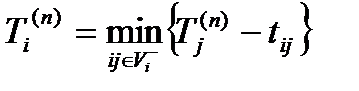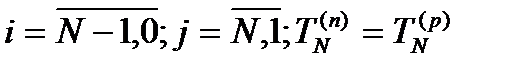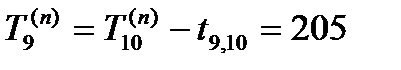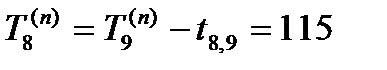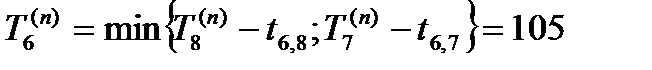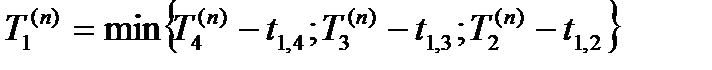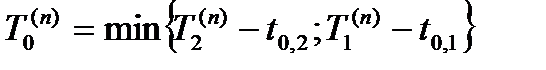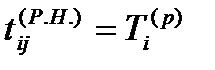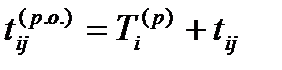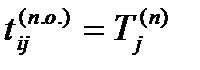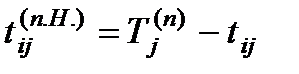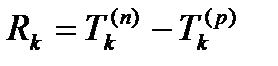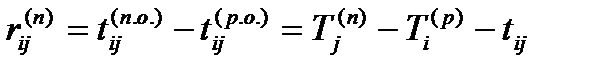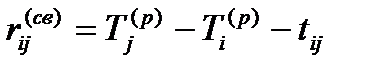Параметры сетевой модели
Исходная информация для модели включает сеть, продолжительности tij всех работ (i, j), момент начала выполнения комплекса Т 0, а также может содержать (но не обязательно) директивный срок Тдир наступления завершающего события. Продолжительности работ задаются как детерминированные неотрицательные величины.
Одна из основных задач управления состоит в составлении плана выполнения комплекса работ. Параметрами плана, определяемыми с помощью сетевой модели, являются лишь временные характеристики: моменты начала и окончания каждой работы и всего комплекса работ. Их называют параметрами сетевой модели.
Важнейшим параметром является критическое время Tкр – минимальное время, за которое может быть выполнен весь комплекс. Критическому времени соответствует критический путь Lкр, то есть полный путь, продолжительность которого и составляет критическое время: t (Lкр)= Ткр. Очевидно, что продолжительность любого другого полного пути равна или меньше критического времени Ткр, поэтому критический путь можно определить, как путь, имеющий максимальную продолжительность.
Работы, лежащие на критическом пути, называются критическими работами. Именно они определяют время выполнения комплекса в целом, поэтому ход их выполнения имеет особую важность при управлении выполнением всего комплекса.
В плане выполнения всего комплекса должны быть определены моменты наступления всех событий, начала и окончания работ. Как правило, эти моменты устанавливаются не однозначно, а располагаются в некотором диапазоне. При анализе сетевой модели определяются параметры, ограничивающие эти диапазоны. Такими параметрами для каждого k- го события являются ранний срок наступления события Tk ( p ) и поздний срок наступления события Tk ( n ) . Используя эти параметры, можно вычислить и другие параметры, в том числе критическое время Tкр и критический путь Lкр, на основании которых составляется план выполнения комплекса. Поэтому начнем с рассмотрения параметров Tk ( p ) и Tk ( n ) .
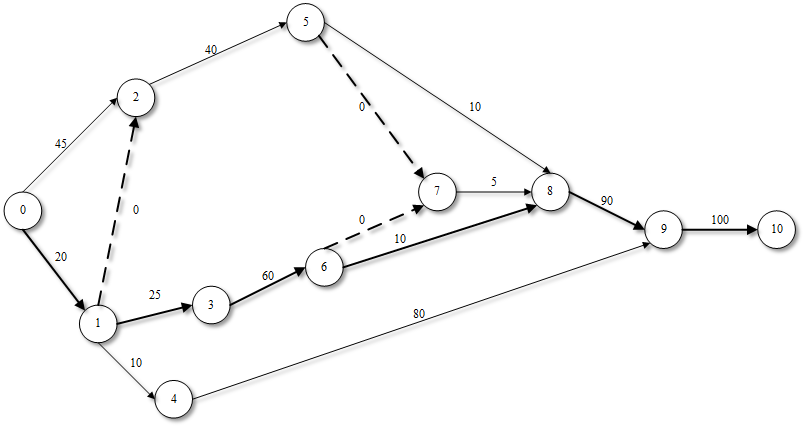
На рис. 2 изображена сетевая модель, используемая далее при изложении методики расчета параметров сетевых моделей.
Ранний срок наступления события Tk ( p ) – это самый ранний из возможных моментов наступления данного k -го события, и определяется он временем, необходимым для выполнения всех предшествующих ему работ.
Очевидно, что событие может наступить только тогда, когда будут выполнены все работы максимального по продолжительности пути. Поэтому значение Tk ( p ) и определяется как продолжительность максимального из путей, ведущих от основного события к k- му:
(5)
где нулем обозначен номер исходного события.
Например, к событию 7 (рис. 1.2) ведут три пути: 0–1–3–6–7, продолжительность которого равна 105 единицам времени; 0–1–2–5–7 с продолжительностью 60 ед. и 0–2–5–7 с продолжительностью 85 ед.
Очевидно, что событие 7 может наступить не раньше чем через 105 ед. времени после исходного события, поэтому T7 ( p ) = 105 ед.
Из сформулированных понятий раннего и позднего сроков наступления событий следует, что для завершающего события
(6)
Напишем формулу для вычисления Tk ( n ) . Обозначим через Vi ̅ множество дуг (i,j), выходящих из i -й вершины, и допустим, что все значения Tj ( n ) для j -х событий, которыми заканчивается каждая из дуг, уже вычислены.
Тогда на основании формул (5) и (6) можно написать:
(7)
Вычисляя с помощью формулы (7) значения Ti ( n ) (вычисления ведутся последовательно от завершающего события к исходному), получим для нашей сетевой модели (рис. 2)
Зная ранние и поздние сроки наступления событий, можно вычислить для каждой работы (i,j):
– ранний срок начала tij ( P . H .) ;
– ранний срок окончания tij ( p . o .) ;
– поздний срок начала tij ( n . H .) ;
– поздний срок окончания tij ( n . o .) .
Первые два параметра – это самые ранние из возможных моментов начала и окончания данной работы. Очевидно, что ранний срок начала работы совпадает с ранним сроком наступления ее начального события, а ранний срок окончания превышает его на величину продолжительности работы (i, j):
(8)
(9)
Вторые два параметра обозначают самые поздние из допустимых моментов начала и окончания данной работы, при которых еще возможно выполнение всех следующих работ без превышения критического времени. Поздний срок окончания работы совпадает с поздним сроком наступления ее конечного события, а поздний срок начала — меньше на величину tij:
(10)
(11)
Важными параметрами сетевой модели являются резервы времени событий и работ. Резервы времени существуют в сетевой модели во всех случаях, когда имеется более одного пути разной продолжительности.
Резерв времени события R — это такой промежуток времени, в пределах которого может меняться момент наступления события без превышения критического времени.
Величина Rk определяется как разность:
(12)
где k – номер события
Исходное, завершающее событие, а также все события, лежащие на критическом пути, резервами времени не располагают. Отсюда простой способ нахождения критического пути: определить события, не имеющие резерва времени, через них и пройдет критический путь.
Для работ можно рассматривать различные виды резервов, из которых наиболее важными являются:
(13)
представляющий максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы (i,j), не изменяя срок наступления завершающего события;
(14)
представляющий собой максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы, не изменяя при этом ранние сроки наступления всех следующих событий.
Полный резерв времени работы принадлежит всему пути, на котором эта работа лежит. Если этот резерв использовать полностью для увеличения длительности данной работы или какой-либо другой работы данного пути, то остальные работы пути останутся без резервов.
Работы, у которых полный резерв отличается от полного резерва критических работ (то есть от rij ( n ) =0) не более чем на заданную величину d, называются подкритическими. При небольших отклонениях в сроках выполнения подкритические работы становятся критическими, поэтому при управлении комплексом нужно наряду с критическими уделять особое внимание и подкритическим работам.
Множество всех критических и подкритических работ называют критической зоной комплекса.
Вопросы для самопроверки по 1 разделу
1. Дайте определение сетевой модели.
2. Что называется сетевым графиком?
3. Что означает понятие «действительная работа»?
4. Чему равна продолжительность фиктивной работы?
5. Какое событие называется завершающим?
6. Что называется путем в сетевой модели?
7. Что понимается под полным путем?
8. Какой ранг присваивается исходному событию в методе разделения событий на ранги?
9. В чем суть метода последовательного вычеркивания дуг?
10. Какие модели являются оптимизационными?
11. С помощью каких моделей можно найти минимальное время, в течение которого может быть выполнен весь комплекс, и определить календарные сроки начала и окончания каждой работы комплекса, обеспечивающие выполнение всего комплекса в найденное минимальное время?
12. Какие оценки продолжительности выполнения отдельных работ вы знаете?
13 Какая сетевая модель называется детерминированной?
14. Какая сетевая модель называется вероятностной?
15. В каких случаях используют для оценки продолжительности работы бета-распределение?
16. Какие вероятностные оценки используют в системах сетевого планирования и управления?
17. Что представляют собой первичные сетевые модели?
18. Что представляют собой частные сетевые модели?
19. Что представляют собой комплексные сетевые модели?
20. Какие правила должны соблюдаться при укрупнении людьми?
21. Какие параметры сетевой модели с учетом временных характеристик вы знаете?
22. Какие работы называются критическими?
23 Дайте определение резерву времени события и работ.
24. Какие работы называются подкритическими?
25. Какие методы расчета параметров сетевой модели вы знаете?
26. В чем суть матричного метода?
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
2.6. Основные параметры сетевой модели
К основным параметрам сетевой модели относятся: критический путь, резервы времени событий и работ. Эти параметры являются исходными для получения ряда дополнительных характеристик, а также для анализа модели.
Критический путь — это наибольший по продолжительности путь сетевой модели от исходного события до завершающего.
В сетевой модели имеются и другие пути, опирающиеся, на исходное и завершающее событие (полные пути), которые могут либо полностью проходить вне критического пути, либо частично совпадать с критической последовательностью работ. Эти пути называются ненапряженными.
Ненапряженные пути — эта полные пути сетевой модели, которые по продолжительности меньше критического пути.
Ненапряженные пути обладают важным свойством: на участках, не совпадающих с критической последовательностью работ они имеют резервы времени. Это означает, что задержка в совершении событий, не лежащих на критическом пути, до определенного момента не влияет на срок завершения разработки в целом. Критические пути резервами времени не располагают.
Поздний срок свершения i-го события — это такой срок свершения i-го события, превышение которого вызовет задержку завершающего события.
Поздний срок свершения i-го события определяется разностью между продолжительностью критического пути и максимального из последующих за данным событием путей до завершающего события:
Тпi = t(Lкр) – t[L(i C) max]
Ранний срок свершения i-го события — минимальный срок, необходимый для выполнения всех работ, предшествующих данному событию.
Ранний срок свершения i-го события определяется как продолжительность во времени максимального из путей, ведущих от исходного события I до данного события i:
Трi = t[L(Ii) max
Резерв времени события — это такой промежуток времени, на который может быть отсрочено свершение события без нарушения сроков завершения разработки в целом.
Резерв времени i-го события определяется как разность между поздним Тпi и ранним Трi, сроками наступления события:
Путь, соединяющий события с нулевыми резервами времени, является критическим.
Резервами времени располагают также работы. Зная ранние и поздние сроки наступления событий, можно для любой работы (i,j) определить ранние и поздние сроки начала и окончания работы.
Ранний срок начала работы (i,j) — минимальное необходимое время между моментом наступления исходного события и моментом начала этой работы.
Ранний срок начала работы (i,j) определяется по формуле:
Поздний срок начала работы (i,j) — максимально допустимый момент начала работы, при котором еще возможно выполнение данной работы и всех следующих за ней работ без превышения критического времени выполнения комплекса работ.
Поздний срок начала работы (i,j) определяется по формуле:
Ранний срок окончания работы (i,j) — минимальное необходимое время между моментом наступления исходного события и моментом окончания этой работы.
Ранний срок окончания работы (i,j) определяется по формуле:
Поздний срок окончания работы (i,j) — максимально допустимый момент окончания данной работы, при котором еще возможно выполнение всех следующих за ней работ без превышения критического времени выполнения комплекса работ.
Поздний срок окончания работы (i,j) определяется по формуле:
Полный резерв времени пути — это разница во времени между длиной критического пути t(Lкр) и длиной любого другого пути t(Ls).
Полный резерв времени пути показывает, насколько могут быть увеличены продолжительности всех работ, принадлежащих пути Ls.
Полный резерв времени пути определяется по формуле:
Полный резерв времени работы Rп ij — максимальное время, на которое можно увеличить продолжительность работы (i,j) или отсрочить ее начало без нарушения позднего срока наступления ее конечного события, не изменяя при этом продолжительности критического пути.
У отдельных работ помимо полного резерва времени имеется свободный резерв времени Rсij, являющийся частью полного резерва.
Свободный резерв времени работы Rс ij — максимальное время, на которое можно увеличить продолжительность работы (i,j) или отсрочить ее начало без нарушения ранних сроков наступления всех последующих событий и работ.
Резервы времени, особенно свободный, позволяют маневрировать сроками начала и окончания работ, их продолжительностью.