Перераспределение ресурсов в сетевых моделях

8. Коэффициент напряженности работы. Анализ и оптимизация сетевого графика

Прежде чем использовать сетевой график как основной инструмент управления ходом работ, необходимо провести его анализ и оптимизацию. Анализ и оптимизация сетевого графика в системах СПУ, в которых объектом планирования и контроля являются сроки выполнения работ (а именно такие графики мы и рассматриваем), в основном сводится к сокращению продолжительности критического пути.

Анализ сетевого графика выполняется с целью, во-первых, проверки правильности оценки времени критических работ и работ, имеющих минимальные резервы времени; во-вторых, сравнения установленного срока выполнения комплекса работ со сроком, полученным в результате расчета временных параметров сетевого графика. Главная цель анализа сети с временной оценкой работ состоит в определении наиболее целесообразных способов достижения оптимальных сроков выполнения комплекса работ.

Основное внимание в сетевом графике необходимо обращать на критические работы. Увеличение или уменьшение продолжительности критических работ, а, следовательно, и критического пути может привести к изменению срока завершения комплекса работ в целом. Для выполнения запланированного комплекса работ в заданный срок необходимо не только увязать этот срок с рассчитанным по сетевому графику (в случае, когда заданный срок оказался меньше расчетного, т.е. меньше ), с отпущенными материальными и трудовыми ресурсами, но и так организовать выполнение работ, чтобы составленный с помощью сетевого графика план стал реальностью.

Для оптимизации сетевой модели, выражающейся в перераспределении ресурсов с ненапряженных работ на критические для ускорения их выполнения, необходимо как можно более точно оценить степень трудности своевременного выполнения всех работ, а также «цепочек» пути. Более точным инструментом решения этой задачи по сравнению с полным резервом является коэффициент напряженности, который может быть вычислен одним из двух способов по формуле:

где — продолжительность максимального пути, проходящего через работу ; — продолжительность (длина) критического пути; — продолжительность отрезка рассматриваемого (максимального пути, проходящего через работу ) пути, совпадающего с критическим путем; — полный резерв времени работы

Коэффициент напряженности может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути). Чем ближе к 1 коэффициент напряженности, тем сложнее выполнить данную работу в установленные сроки. Чем ближе коэффициент напряженности к 0, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу.

На основе коэффициента напряженности все работы сетевого графика могут быть разделены на три группы:

В результате перераспределения ресурсов стараются максимально уменьшить общую продолжительность работ, что возможно при переводе всех работ в первую группу.

Оптимизация сетевого графика представляет процесс улучшения организации выполнения комплекса работ с учетом срока его выполнения. Оптимизация проводится с целью сокращения длины критического пути, выравнивания коэффициентов напряженности работ, рационального использования ресурсов.

В первую очередь принимаются меры по сокращению продолжительности работ, находящихся на критическом пути. Это достигается:

• перераспределением всех видов ресурсов, как временных (использование резервов времени некритических путей), так и трудовых, материальных, энергетических; при этом перераспределение ресурсов должно идти, как правило, из зон, менее напряженных, в зоны, объединяющие наиболее напряженные работы;
• сокращением трудоемкости критических работ за счет передачи части работ на другие пути, имеющие резервы времени;
• параллельным выполнением работ критического пути;
• пересмотром топологии сети, изменением состава работ и структуры сети.

В процессе сокращения продолжительности работ критический путь может измениться, и в дальнейшем процесс оптимизации будет направлен на сокращение продолжительности работ нового критического пути и так будет продолжаться до получения удовлетворительного результата. В идеале длина любого из полных путей может стать равной длине критического пути или по крайней мере пути критической зоны. Тогда все работы будут вестись с равным напряжением, а срок завершения проекта существенно сократится.

Для рис. 8 определить характеристики СПУ:

1) ранние и поздние сроки совершения событий;

2) резервы времени событий;

3) критический путь и его длину, пояснить смысл найденной величины (длина критического пути);

4) для некритических работ найти полные, свободные и независимые резервы времени;

5) для некритических работ найти коэффициенты напряженности и пояснить за счет каких работ возможна оптимизация сетевой модели.

Источник

Коэффициент напряженности работы в сетевой модели. Пути снижения напряженности работ.

Прежде чем использовать сетевой график как основной инструмент управления ходом работ, необходимо провести его анализ и оптимизацию. Анализ и оптимизация сетевого графика в системах сетевого планирования и у равления (СПУ), в основном сводится к сокращению продолжительности критического пути. Основное внимание в сетевом графике необходимо обращать на критические работы. Увеличение или уменьшение продолжительности критических работ, а, следовательно, и критического пути может привести к изменению срока завершения комплекса работ в целом. Для оптимизации сетевой модели, выражающейся в перераспределении ресурсов с ненапряженных работ на критические для ускорения их выполнения, необходимо как можно более точно оценить степень трудности своевременного выполнения всех работ, а также «цепочек» пути. 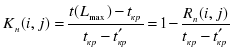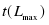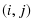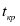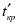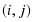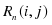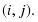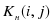Более точным инструментом решения этой задачи по сравнению с полным резервом является коэффициент напряженности, который может быть вычислен одним из двух способов по формуле: где — продолжительность максимального пути, проходящего через работу ; — продолжительность (длина) критического пути; — продолжительность отрезка рассматриваемого (максимального пути, проходящего через работу ) пути, совпадающего с критическим путем; — полный резерв времени работы Коэффициент напряженности может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути). Чем ближе к 1 коэффициент напряженности, тем сложнее выполнить данную работу в установленные сроки. Чем ближе коэффициент напряженности к 0, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу. В результате перераспределения ресурсов стараются максимально уменьшить общую продолжительность работ, что возможно при переводе всех работ в первую группу. Оптимизация сетевого графика представляет процесс улучшения организации выполнения комплекса работ с учетом срока его выполнения. Оптимизация проводится с целью сокращения длины критического пути, выравнивания коэффициентов напряженности работ, рационального использования ресурсов. В первую очередь принимаются меры по сокращению продолжительности работ, находящихся на критическом пути. Это достигается: —перераспределением всех видов ресурсов, как временных (использование резервов времени некритических путей), так и трудовых, материальных, энергетических; при этом перераспределение ресурсов должно идти, как правило, из зон, менее напряженных, в зоны, —объединяющие наиболее напряженные работы; —сокращением трудоемкости критических работ за счет передачи части работ на другие пути, имеющие резервы времени;-параллельным выполнением работ критического пути; -пересмотром топологии сети, изменением состава работ и структуры сети.

Коэффициенты прямых и косвенных материальных затрат в матричных моделях баланса. Основные уравнения математической модели балансового метода планирования.

1. Краткая характеристика методов решения систем уравнений матричных моделей балансового метода планирования (метод Жордана-Гаусса, метод простых итераций, итерационный метод Зейделя). Достаточный признак сходимости итерационных процессов.

Для продолжения скачивания необходимо пройти капчу:

Источник