Помогите построить сетевую модель

Тонкости построения сетевых моделей в Python

Что является основным инструментом, который использует руководитель при управлении проектом? Принято считать, что основным инструментом руководителя проекта является календарный план, в основе которого лежит сетевая модель работ по проекту. Однажды мне довелось реализовать сетевую модель работ на языке Python (код и описание здесь). Ниже приведены уроки, извлеченные по результатам проделанной работы.

Сначала создай работы, потом устанавливай связи

При построении сетевой модели часто возникает вопрос, в каком порядке создавать работы и устанавливать связи между ними? Наиболее очевидным является двухэтапный подход – сначала создаются все работы модели, затем между ними устанавливаются связи. Такой подход позволяет избежать ошибок типа KeyError: ‘101’, возникающих при параллельном выполнении этих двух операций, когда система пытается установить связь с работой, которая еще не была создана.

Конечно, суммарное время выполнения двух последовательных операций по созданию работ и установке связей между ними может быть оптимизировано за счет использования алгоритма, в котором эти операции выполняются параллельно. Однако даже на больших моделях с десятком тысяч работ последовательные алгоритмы работают достаточно быстро. Поэтому в условиях временных ограничений на реализацию проекта вполне можно обойтись классическим двухэтапным подходом.

Пересчитывай модель после её построения

Стоит ли выполнять пересчет всякий раз, когда происходит установка связи между работами при построении сетевой модели? С одной стороны, постоянный пересчет позволяет держать модель в актуальном состоянии. С другой, пересчет увеличивает время ее построения.

Для сравнения были реализованы две функции:

1. build_model_by_method() – построение с пересчетом модели;
2. build_model_by_assignment() – построение без пересчета модели.

from predict import Activity import xml.etree.ElementTree as ET import sys import timeit from timeit import Timer # вычисляем значение параметра задачи def get_child(child, activity_field): text = child.find(activity_field).text if text is None: return None return int(text) # строим модель с использованием метода пересчета def build_model_by_method(filename): sys.setrecursionlimit(10000) f = open(filename,'r') tree = ET.parse(f) root = tree.getroot() schedule = <> next = <> for child in root.findall('Activity'): start_date = get_child(child,'start_date') finish_date = get_child(child,'finish_date') duration = get_child(child,'duration') not_early_date = get_child(child,'not_early_date') a = Activity(id, start_date, finish_date, duration, not_early_date) schedule[id] = a next_activity = '' if child.find('next_activity').text is None else child.find('next_activity').text next[id] = next_activity for key in schedule: if nextПомогите построить сетевую модель != '': for next_id in nextПомогите построить сетевую модель.split(';'): scheduleПомогите построить сетевую модель.append_next(schedule[next_id]) sys.setrecursionlimit(1000) # строим модель без использования метода пересчета def build_model_by_assignment(filename): f = open(filename,'r') tree = ET.parse(f) root = tree.getroot() schedule = <> next = <> for child in root.findall('Activity'): start_date = get_child(child,'start_date') finish_date = get_child(child,'finish_date') duration = get_child(child,'duration') not_early_date = get_child(child,'not_early_date') a = Activity(id, start_date, finish_date, duration, not_early_date) schedule[id] = a next_activity = '' if child.find('next_activity').text is None else child.find('next_activity').text next[id] = next_activity for key in schedule: if nextПомогите построить сетевую модель != '': for next_id in nextПомогите построить сетевую модель.split(';'): scheduleПомогите построить сетевую модель.next_activity.append(schedule[next_id]) # считаем скорость построения модели print('Test for 100 activities:') t1 = Timer("build_model_by_method('data/activity_100.xml')", "from __main__ import build_model_by_method") print("build_model_by_method", t1.timeit(number = 1000)) t2 = Timer("build_model_by_assignment('data/activity_100.xml')", "from __main__ import build_model_by_assignment") print("build_model_by_assignment", t2.timeit(number = 1000)) print('Test for 1000 activities') t3 = Timer("build_model_by_method('data/activity_1000.xml')", "from __main__ import build_model_by_method") print("build_model_by_method", t3.timeit(number = 1000)) t4 = Timer("build_model_by_assignment('data/activity_1000.xml')", "from __main__ import build_model_by_assignment") print("build_model_by_assignment", t4.timeit(number = 1000)) print('Test for 10000 activities') t5 = Timer("build_model_by_method('data/activity_10000.xml')", "from __main__ import build_model_by_method") print("build_model_by_method", t5.timeit(number = 1000)) t6 = Timer("build_model_by_assignment('data/activity_10000.xml')", "from __main__ import build_model_by_assignment") print("build_model_by_assignment", t6.timeit(number = 1000)) 

$ python network.py Test for 100 activities: build_model_by_method 1.7820062519999738 build_model_by_assignment 1.426311435999878 Test for 1000 activities build_model_by_method 18.998158786999966 build_model_by_assignment 14.216093206999858 Test for 10000 activities build_model_by_method 249.93449528199994 build_model_by_assignment 148.85600239800033 

Как видно, чем больше работ, тем медленнее работает функция построения сетевой модели с использованием пересчета по сравнению с функцией, в которой пересчет не используется.

Контролируй глубину рекурсии

Сетевая модель проекта состоит из работ и связей между ними. В отсутствии дополнительной информации о сети для ее пересчета используются рекурсивные алгоритмы. Такие алгоритмы состоят в последовательном проходе по работам сети и пересчете их параметров (например, длительности, дат начала и окончания). Чем больше работ в сети, тем больше глубина рекурсии.

Известно, что в Python по умолчанию установлено ограничение на глубину рекурсии – не больше 1000 рекурсивных вызовов. Для получения этого ограничения предназначен метод getrecursionlimit() модуля sys.

>>> import sys >>> sys.getrecursionlimit() 1000

При работе с большими сетями, число работ в которых измеряется десятками тысяч, обычной ситуацией является превышение глубины рекурсии и, как следствие, возникновение ошибки типа RecursionError: maximum recursion depth exceeded in comparison. Ошибка приводит к остановке построения либо пересчета модели и падению системы.

Чтобы предотвратить ошибку, построить и пересчитать большую сеть, необходимо увеличить ограничение на глубину рекурсии. И в этом нам поможет метод setrecursionlimit() модуля sys.

 >>> import sys >>> sys.setrecursionlimit(10000) >>> sys.getrecursionlimit() 10000

До какого значения требуется увеличить глубину рекурсии? Ответ на этот вопрос зависит от структуры сетевой модели. Если структура неизвестна или достаточно сложна, рекомендую устанавливать ограничение в значение, равное количеству работ в сети. Рекурсивный алгоритм проходится либо по всем либо по части работ. Поэтому глубина рекурсии не должна превысить количество работ в сети.

И напоследок…

Управление проектами – это модно. Но модно еще не значит эффективно. На рынке существуют программные решения по пересчету сетевых моделей, такие как Microsoft Project. Однако алгоритмы, зашитые в них остаются доступными только вендерам соответствующего программного обеспечения.

Настоящая статья написана на основе опыта разработки открытого модуля по построению и пересчету сетевых моделей проектов. Я надеюсь, что приведенные в статье извлеченные уроки будут полезны читателю как с теоретической, так и с чисто практической точки зрения. Если настоящая статья вызовет интерес, то я поделюсь новыми знаниями, которые возникнут в дальнейшем, по мере развития модуля.

Источник

2. Правила построения сетевых моделей

В сетевой модели должна отражаться технологическая последовательность и очерёдность отдельных работ. Модель должна иметь простую форму. Стрелки должны быть направлены слева направо от события с меньшим номером к событию с большим номером, необходимо стремиться к минимальному пересечению отдельных работ.

2.1. Основные правила

1. Правило составных работ – любая работа а может быть разбита на составляющие, если после частичного выполнения её можно начать следующую работу б. При этом вводятся логические зависимости и дополнительные события (рис. 4).

2. Правило параллельных работ – если между двумя событиями необходимо показать две или несколько работ, которые выполняются параллельно, в модели вводятся дополнительное событие по окончании одной из параллельных работ и логическая зависимость (фиктивная работа) между ними (рис. 5).

3. Правило зависимых и независимых работ – если для начала одной работыг необходимо выполнение всех пред-шествующих работ a и б, а для начала работы в необходимо выполнение только работы a, то вводятся дополнительное событие и логическая зависимость (рис. 6).

4. Правило запрещения замкнутых контуров, т.е. один путь не должен дважды проходить через одно событие (рис. 7).

5. Правило запрещения тупиковых событий, т.е. событий, из которых не выходит ни одна работа, если событие не завершающее (рис. 8).

6. Правило запрещения необеспеченных событий, т.е. со- бытий, в которые не входит ни одна работа, если событие не исходное (рис. 9).

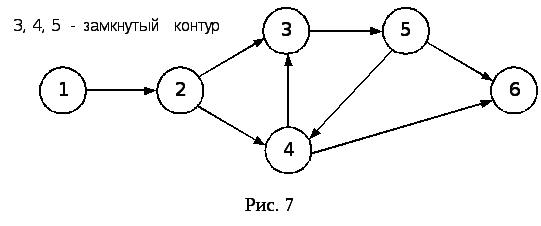
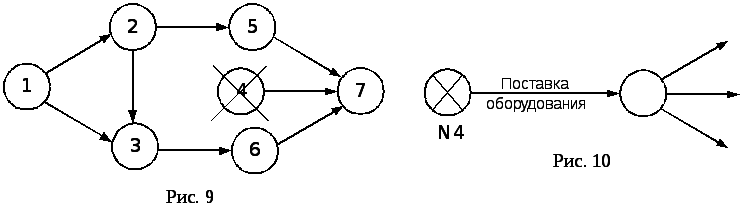
7. Правило изображения поставки (рис. 10).

2.2. Построение сетей

Для построения сетевой модели нужно знать технологию работ и зависимость одних работ от других. Последовательность выполнения работ записывается в форме таблицы, в которой указывается зависимость данной работы ig от предшествующей hi.

Пример 1. По данной зависимости работ построить сетевую модель.

Источник

1.3.5. Пример построения и расчета сетевой модели

Исходные данные варианта лабораторной работы включают название и продолжительность каждой работы (табл. 1.1), а также описание упорядочения работ.

1. Работы C, I, Gявляются исходными работами проекта, которые могут выполняться одновременно.
2. Работы E иAследуют за работойC.
3. Работа Hследует за работойI.
4. Работы D иJследуют за работойG.
5. Работа Bследует за работойE.
6. Работа Kследует за работамиAиD, но не может начаться прежде, чем не завершится работаH.
7. Работа Fследует за работойJ.

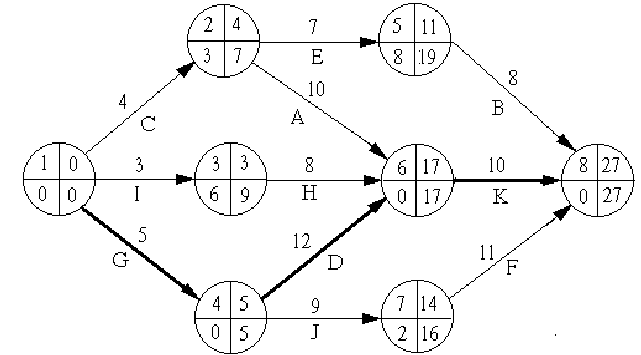
На рис.1.4 представлена сетевая модель, соответствующая данному упорядочению работ. Каждому событию присвоен номер, что позволяет в дальнейшем использовать не названия работ, а их коды (см. табл. 1.2). Численные значения временных параметров событий сети вписаны в соответствующие секторы вершин сетевого графика, а временные параметры работ сети представлены в табл. 1.3. Таблица 1.2 Описание сетевой модели с помощью кодирования работ

Номера событий		Код работы	Продолжительность
начального	конечного	работы
1	2	(1,2)	4
1	3	(1,3)	3
1	4	(1,4)	5
2	5	(2,5)	7
2	6	(2,6)	10
3	6	(3,6)	8
4	6	(4,6)	12
4	7	(4,7)	9
5	8	(5,8)	8
6	8	(6,8)	10
7	8	(7,8)	11

Рис.1.4. Сетевая модель Таблица 1.3 Временные параметры работ

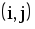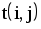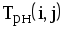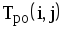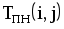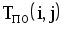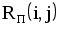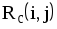1,2	4	0	4	3	7	3	0
1,3	3	0	3	6	9	6	0
1,4	5	0	5	0	5	0	0
2,5	7	4	11	12	19	8	0
2,6	10	4	14	7	17	3	3
3,6	8	3	11	9	17	6	6
4,6	12	5	17	5	17	0	0
4,7	9	5	14	7	16	2	0
5,8	8	11	19	19	27	8	8
6,8	10	17	27	17	27	0	0
7,8	11	14	25	16	27	2	2

1.4. Контрольные вопросы

1.4.1. Зачетный минимум

1. Определение события, виды событий, практические примеры событий, обозначение событий на графике, временные параметры событий.
2. Определение работы, классификация работ с приведением соответствующих практических примеров, обозначение работ на графике, временные параметры работ.
3. Правила построения сетевых графиков.
4. Определение пути в сетевом графике, виды путей, важность определения критического пути.
5. Умение вычислять временные параметры событий и работ.

1.4.2. Дополнительные вопросы

1. Почему при расчете раннего срока свершения события iвыбираютмаксимальнуюиз сумм ?
2. Почему при расчете позднего срока свершения события iвыбираютминимальнуюиз разностей ?
3. Какова взаимосвязь полного и свободного резервов работы?
4. Как можно найти критических путь в сетевой модели, без непосредственного суммирования длительностей работ?

Часть 2. ОПТИМИЗАЦИЯ СЕТЕВЫХ МОДЕЛЕЙ ПО КРИТЕРИЮ «МИНИМУМ ИСПОЛНИТЕЛЕЙ» 2.1. ЦЕЛЬ РАБОТЫ Знакомство с методикой и приобретение навыков проведения оптимизации сетевых моделей по критерию «Минимум исполнителей». 2.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Согласно номеру своего варианта получите данные о количество исполнителей, занятых на каждой работе сетевой модели, и ограничение по численности Nодновременно занятых в работе исполнителей. 2. Постройте в отчете графики привязки и загрузки, используя нормальные длительности работ сети — 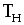(см. п.2.3.1), и покажите их преподавателю. 3. Проверьте правильность построения графиков привязки и загрузки с помощью компьютера, в случае необходимости выявите и устраните ошибки. 4. Используя компьютерную программу, проведите уменьшение численности исполнителей, одновременно занятых на работах сети, до требуемого уровня N. 5. Отчет по лабораторной работе должен содержать:

• номер варианта;
• исходные данные варианта;
• графики привязки и загрузки до проведения оптимизации загрузки;
• графики привязки и загрузки после проведения оптимизации загрузки (возможно использование пунктирных линий на первоначально построенных графиках для отображение изменений в привязке работ и загрузке сети, вызванных сдвигами работ);
• коды работ, сдвинутых в процессе оптимизации, и время их сдвига.

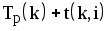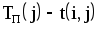Источник