Понятие о критическом пути сетевых моделей

1. Основные понятия сетевой модели

Сетевая модель — графическое изображение плана выполнения комплекса работ, состоящего из нитей (работ) и узлов (событий), которые отражают логическую взаимосвязь всех операций. В основе сетевого моделирования лежит изображение планируемого комплекса работ в виде графа.

Граф — схема, состоящая из заданных точек (вершин), соединенных линиями. Отрезки, соединяющие вершины, называются ребрами (дугами) графа.

Ориентированным называется такой граф, на котором стрелкой указаны направления всех его ребер, что позволяет определить, какая из двух его граничных вершин является начальной, а какая — конечной. Исследование таких сетей проводится методами теории графов.

Теория графов оперирует понятием пути, объединяющим последовательность взаимосвязанных ребер. Контур означает такой путь, у которого начальная вершина совпадает с конечной. Сетевой график — это ориентированный граф без контуров. В сетевом моделировании имеются два основных элемента — работа и событие.

Работа — это активный процесс, требующий затрат ресурсов, либо пассивный (ожидание), приводящий к достижению намеченного результата.

Фиктивная работа — это связь между результатами работ (событиями), не требующая затрат времени и ресурсов.

Событие — это результат (промежуточный или конечный) выполнения одной или нескольких предшествующих работ.

Путь — это любая непрерывная последовательность (цель) работ и событий.

Критический путь — это путь, не имеющий резервов и включающий самые напряженные работы комплекса. Работы, расположенные на критическом пути, называют критическими. Все остальные работы являются некритическими (ненапряженными) и обладают резервами времени, которые позволяют передвигать сроки их выполнения, не влияя на общую продолжительность выполнения всего комплекса работ.

При построении сетевых моделей необходимо соблюдать следующие правила.

1. Сеть изображается слева направо, и каждое событие с большим порядковым номером изображается правее предыдущего. Общее направление стрелок, изображающих работы, также в основном должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером.
2. Два соседних события могут объединяться лишь одной работой. Для изображения параллельных работ вводятся промежуточное событие и фиктивная работа (рис. 27-1).
3. В сети не должно быть тупиков, т.е. промежуточных событий, из которых не выходит ни одна работа (рис. 27.2).
4. В сети не должно быть промежуточных событий, которым не предшествует хотя бы одна работа (рис. 27.3).
5. В сети не должно быть замкнутых контуров, состоящих из взаимосвязанных работ, создающих замкнутую цепь (рис. 27.4).

Для правильной нумерации событий поступают следующим образом: нумерация событий начинается с исходного события, которому дается номер 1. Из исходного события 1 вычеркивают все исходящие из него работы, на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию дается номер 2. Затем вычеркивают работы, выходящие из события 2, и вновь находят на оставшейся части сети событие, в которое не входит ни одна работа, ему присваивается номер 3, и так продолжается до завершающего события. Продолжительность выполнения работ устанавливается на сновании действующих нормативов или по экспертным оценкам специалистов. В первом случае временные оценки являются детерминированными (однозначными), во втором — стохастическими (вероятностными).

Источник

Определение критического пути

Будем предполагать, что время выполнения каждой работы точно известно. Введем следующие определения.

Путь— последовательность взаимосвязанных работ, ведущая из одной вершины проекта в другую вершину. Например (см. Рисунок 48), и – два различных пути.

Рисунок 48. Различные пути на сетевом графике

Длина пути— суммарная продолжительность выполнения всех работ пути.

Полный путь— это путь от исходного к завершающему событию.

Критический путь— полный путь, суммарная продолжительность выполнения всех работ которого является наибольшей.

Очевидно, что минимальное время, необходимое для выполнения любого проекта равно длине критического пути. Именно на работы, принадлежащие критическому пути, следует обращать особое внимание. Если такая работа будет отложена на некоторое время, то время окончания проекта будет отложено на то же время. Если необходимо сократить время выполнения проекта, то в первую очередь нужно сократить время выполнения хотя бы одной работы на критическом пути.

Для того, чтобы найти критический путь, достаточно перебрать все пути и выбрать тот, или те из них, которые имеют наибольшую суммарную продолжительность выполнения работ. Однако для больших проектов реализация такого подхода связана с вычислительными трудностями. Метод критического пути (метод CPM — Critical Path Method) позволяет получить критический путь намного проще.

Расчет сетевой модели начинают с временных параметров событий, которые вписывают непосредственно в вершины сетевого графика (Рисунок 49):

• –ранний срок наступления события i, минимально необходимый для выполнения всех работ, которые предшествуют событию i;
• –поздний срок наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
• –резерв события i, т.е. время, на которое может быть отсрочено наступление события i без нарушения сроков завершения.

Рисунок 49. Параметры событий Ранние сроки наступления событий рассчитываются от исходного (S) к завершающему (F) событию следующим образом:

1. для исходного события S: ;
2. для всех остальных событий i: ,

где максимум берется по всем работам (k,i), входящим в событие i; — длительность работы (k,i) (см. Рисунок 50). Рисунок 50. Ранние сроки наступления событий Поздние сроки наступления событий рассчитываются от завершающего к исходному событию:

1. для завершающего события F: ;
2. для всех остальных событий i: ,

где минимум берется по всем работам (i,j), выходящим из события i; — длительность работы (i,j) (см. Рисунок 51). Рисунок 51. Поздние сроки наступления событий Условия критичности пути:

• необходимое условие: нулевые резервы событий, лежащих на критическом пути ;
• достаточное условие: нулевые полные резервы работ, лежащих на критическом пути .— показывает максимальное время, на которое можно увеличить длительность работы (i,j) или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом.

Пример Рассмотрим пример. Компания разрабатывает строительный проект. Исходные данные по основным операциям проекта представлены в таблице. Нужно построить сетевую модель проекта, определить критические пути и проанализировать, как влияет на ход выполнения проекта задержка работы D на 4 недели.

Работа	Непосредственно предшествующая работа	Длительность, недели
A	—	4
B	—	6
C	A, B	7
D	B	3
E	C	4
F	D	5
G	E,F	3

Сетевой график проекта показан на рисунке ниже (см. Рисунок 52). Рисунок 52. Пример. Сетевой график проекта Согласно необходимому условию два полных пути сетевой модели (см. Рисунок 52) имогут быть критическими. Проверим достаточное условие критичности для работ (1,2) и (1,3) , . Путь , начинающийся с работы (1,3) не является критическим, т.к. поскольку как минимум одна из его работ не является критической. Работа (1,3) имеет ненулевой полный резерв, а значит может быть задержана с выполнением, что недопустимо для критических работ. Таким образом, сетевая модель имеет единственный критический путь длительностью 20 недель. За выполнением работ этого пути необходим особый контроль, т.к. любое увеличение их длительности нарушит срок выполнения проекта в целом. Работа D или (2,5) не является критической, ее полный резерв равен 3-м неделям. Это означает, что при задержке работы в пределах 3-х недель срок выполнения проекта не будет нарушен. Поэтому если согласно условию работа D задержится на 4 недели, то весь проект закончится на 1 неделю позже.

Источник

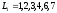
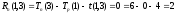
8.5 Сети. Критический путь

Часто приходится решать задачи, в которых каждому ребру заданного графа приписано некоторое положительное (неотрицательное) число (его вес). Обычно, граф нагруженный подобным образом, называется сетью, его вершины – узлами, а ребра – дугами.

Предположим, что требуется проанализировать сложный проект с точки зрения минимальных временных затрат на его выполнение. Для этого проект разбивают на отдельные этапы (работы, операции), оценивают время, необходимое на проведение каждой работы. Составляют таблицу, в которую заносят все виды работ по проекту, их продолжительность и последовательность выполнения.

По данным таблицы строится ориентированная сеть, дуги которой соответствуют работам проекта, а узлы – событиям, обозначающим начало и/или конец этапов. Каждая дуга нагружена числом, равным продолжительности выполнения соответствующей работы. Понятно, что операции, соответствующие дугам, исходящим из произвольного узла сети, не могут начаться прежде, чем закончатся операции, отвечающие дугам, входящим в этот узел.

Подобная сеть называется сетевым графиком проекта или диаграммой работ.

В результате вычерчивания диаграммы работ определяется путь, наибольшей продолжительностью. Этот путь называется критическим. Он и определяет минимальное время выполнения проекта. Работы, входящие в критический путь, называются критическими работами.

Рассмотрим пример построения сетевого графика, определения критического пути и критических работ, а также минимального времени выполнения всех работ.

Составлена таблица последовательности работ проекта, в которой также указаны предшествующие работы и записано время выполнения каждой работы. Построить сетевой график данного проекта.

Источник