Сетевые модели
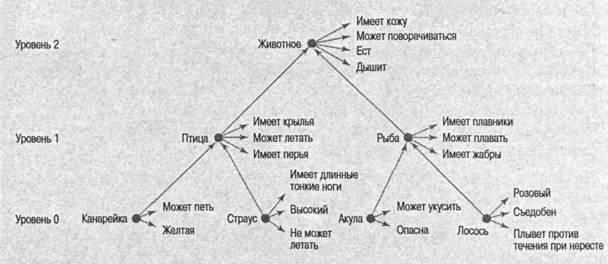
Коллинз и Квиллиан. Из первых сетевых моделей наиболее известна модель, разработанная Алленом Коллинзом и Россом Квиллианом на основе принципов организации памяти в компьютерах (Quillian, 1968, 1969). В этой модели каждое слово помещалось в конфигурацию других слов, хранящихся в памяти, и значение каждого слова представлялось по отношению к другим словам (рис. 9.3). В приведенном примере хранится информация о «канарейке»: это «желтая птица, которая может петь». «Канарейка» входит в категорию или сверхмножество «птица» (что показано стрелкой от «канарейки» к «птице») и обладает свойствами «может петь» и «желтая» (стрелки от канарейки к этим свойствам). В вышестоящем узле общие свойства о птицах собраны вместе («имеют крылья», «могут летать» и «имеют перья»), и такую информацию не надо хранить отдельно для каждой птицы, тогда как информация о рыбе (например, «может плавать» 1 ) должна хранится в другом крыле этой структуры. Высказывание: «Канарейка может летать» оценивается путем
1 Всякий почитатель Джерома Керна знает: «Рыбы должны плавать, а птицы должны летать. »
306 Глава 9, Репрезентация знаний
Рис. 9.3. Гипотетическая структура памяти с трехуровневой иерархией. Адаптировано из: Collins & Quillian, 1969
воспроизведения информации о том, что: (1) канарейка — член сверхмножества птиц; (2) у птицы есть свойство «может летать». В этой системе «пространство», необходимое для хранения информации в семантической памяти, минимизировано за счет того, что каждый элемент — это одно включение, а не несколько. Модель такого типа считается экономичной при конструировании компьютерной памяти.
Модель Коллинза и Квиллиана привлекательна тем, что из нее ясно видно, каким способом воспроизводится информация из семантической памяти. Чтобы провести поиск в памяти с целью оценки конкретного высказывания — например, «Акула может поворачиваться», — мы должны сначала определить, что акула — это рыба, рыба есть животное, а у животного есть свойство «может поворачиваться»; это довольно извилистый путь. Эта модель предполагает также, что для прохода по каждому из путей внутри данной структуры требуется время. Соответственно Коллинз и Квиллиан испытали эту модель, предложив испытуемым оценивать ложность или истинность высказывания и измеряя при этом время, требуемое для такой оценки (зависимая переменная); независимой переменной была семантическая близость элементов в памяти.
Модель Коллинза и Квиллиана предлагает, что семантическая память состоит из обширной сети понятий, которые составлены из единиц и свойств и соединены рядом ассоциативных связей. Несмотря на то что отдельные стороны модели подверглись критике, например то, что сила ассоциативных связей в пределах сети варьирует (так, зависимую категорию «борьба» труднее идентифицировать как вид спорта, чем «бейсбол») или что отдельная ассоциация нарушает когнитивную экономику системы, но это является доводом в пользу модификации системы, а не отказа от нее. Кроме того, модификации этой модели стали хорошей основой для создания последующих моделей.
Как мы увидели, организация знаний в памяти рассматривалась с нескольких точек зрения. Один из таких подходов использовался для объяснения скорости, с которой мы отвечаем на вопросы, подобные приведенным в следующем списке.
Когнитивные модели семантической памяти 307
Теория распространения активации: Коллинз и Лофтус.
Теория распространения активации: Коллинз и Лофтус. Система семантической обработки, которая становится все более влиятельной (особенно среди сторонников коннекционизма) и называется теорией распространения активации, была создана Алланом Коллинзом и Элизабет Лофтус (Collins & Loftus, 1975; см. также Anderson, 1983b). Эта модель, показанная на рис. 9.4, построена на основе сложной сети ассоциаций, в которой определенные воспоминания распределены в пространстве понятий, связаных между собой ассоциациями. На рис. 9.4 показано понятие «красный». Сила связи между понятиями обозначена длиной соединяющих их линий. Длинные линии, такие как между понятиями «красный» и «восходы», указывают на несколько слабую связь; более короткие линии, такие как между понятиями «красный» и «огонь», указывают на более прочную связь. В основе многих моделей репрезентации знаний заложена идея о том, что понятия связаны так же, как в модели Лофтус и Коллинза. Кроме того, имея хоть немного воображения, мы можем представить себе систему нейронных сетей, которые являются воплощением некоторых из особенностей данной модели.
Согласно модели Коллинза и Лофтус, между понятиями распространяется активизация, что может объяснить результаты экспериментов с использованием предварительной подготовки (эффект, в результате которого слово или понятие становится более доступным после предъявления связанного с ним слова, или подготавливающего стимула). Например, если я показываю вам зеленый цвет, вероятно, вы сможете опознать слово «зеленый» быстрее, чем при отсутствии подготавливающего стимула. Кроме того (см. Solso & Short, 1979), если вы видите зеленый цвет, опознание связанных с ним стимулов, например слова «трава», также улучшается. Возможно, будут активизированы даже более отдаленные ассоциации; например, активация может распространяться от одних ассоциаций к другим. В вышеупомянутом примере зеленый цвет подготавливает опознание слова «трава»; однако слово «трава» подготавливает опознание слова «лужайка», даже если единственная связь между зеленым цветом и словом «лужайка» проходит через слово «трава».
1. Основные понятия сетевой модели
Сетевая модель — графическое изображение плана выполнения комплекса работ, состоящего из нитей (работ) и узлов (событий), которые отражают логическую взаимосвязь всех операций. В основе сетевого моделирования лежит изображение планируемого комплекса работ в виде графа.
Граф — схема, состоящая из заданных точек (вершин), соединенных линиями. Отрезки, соединяющие вершины, называются ребрами (дугами) графа.
Ориентированным называется такой граф, на котором стрелкой указаны направления всех его ребер, что позволяет определить, какая из двух его граничных вершин является начальной, а какая — конечной. Исследование таких сетей проводится методами теории графов.
Теория графов оперирует понятием пути, объединяющим последовательность взаимосвязанных ребер. Контур означает такой путь, у которого начальная вершина совпадает с конечной. Сетевой график — это ориентированный граф без контуров. В сетевом моделировании имеются два основных элемента — работа и событие.
Работа — это активный процесс, требующий затрат ресурсов, либо пассивный (ожидание), приводящий к достижению намеченного результата.
Фиктивная работа — это связь между результатами работ (событиями), не требующая затрат времени и ресурсов.
Событие — это результат (промежуточный или конечный) выполнения одной или нескольких предшествующих работ.
Путь — это любая непрерывная последовательность (цель) работ и событий.
Критический путь — это путь, не имеющий резервов и включающий самые напряженные работы комплекса. Работы, расположенные на критическом пути, называют критическими. Все остальные работы являются некритическими (ненапряженными) и обладают резервами времени, которые позволяют передвигать сроки их выполнения, не влияя на общую продолжительность выполнения всего комплекса работ.
При построении сетевых моделей необходимо соблюдать следующие правила.
- Сеть изображается слева направо, и каждое событие с большим порядковым номером изображается правее предыдущего. Общее направление стрелок, изображающих работы, также в основном должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером.
- Два соседних события могут объединяться лишь одной работой. Для изображения параллельных работ вводятся промежуточное событие и фиктивная работа (рис. 27-1).
- В сети не должно быть тупиков, т.е. промежуточных событий, из которых не выходит ни одна работа (рис. 27.2).
- В сети не должно быть промежуточных событий, которым не предшествует хотя бы одна работа (рис. 27.3).
- В сети не должно быть замкнутых контуров, состоящих из взаимосвязанных работ, создающих замкнутую цепь (рис. 27.4).
Для правильной нумерации событий поступают следующим образом: нумерация событий начинается с исходного события, которому дается номер 1. Из исходного события 1 вычеркивают все исходящие из него работы, на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию дается номер 2. Затем вычеркивают работы, выходящие из события 2, и вновь находят на оставшейся части сети событие, в которое не входит ни одна работа, ему присваивается номер 3, и так продолжается до завершающего события. Продолжительность выполнения работ устанавливается на сновании действующих нормативов или по экспертным оценкам специалистов. В первом случае временные оценки являются детерминированными (однозначными), во втором — стохастическими (вероятностными).
Сетевые модели Основные понятия теории графов
Теория графов является эффективным алгоритмом формализации задач экономической и планово-производственной практики. Ее применяют в автоматизации управления производством, календарном и сетевом планировании, при оптимизации размещения производства, рационализации перевозок и т.д.
Представим множество точек на плоскости или в пространстве (вершины графа) и отрезки линий, соединяющих все или некоторые из этих точек. Взаимное расположение, длина, форма этих отрезков не имеют значения.
Если на отрезке указано направление, то он называется дугой.
Если ориентация не указана, отрезок называется ребром.
Совокупность вершин и дуг (ребер) называется графом.
Если концевые вершины дуги (ребра) совпадают, то дугу (ребро) называют петлей.
Дуги и ребра с одинаковыми концевыми вершинами называются параллельными.
ПАРАЛЛЕЛЬНЫЕ ДУГА И РЕБРО
Граф называется конечным, если он содержит конечное число вершин.
Граф называется взвешенным, если каждая дуга (ребро) характеризуется одним или несколькими числами.
Если в графе все отрезки ориентированы, то он называется орграфом.
При изображении графа его вершины можно располагать произвольно и по своему усмотрению выбирать форму соединяющих их линий.
Графы называются изоморфными, если между их вершинами существует такое взаимно однозначное соответствие, при котором две вершины одного графа соединены отрезками тогда и только тогда, когда соответствующие вершины другого графа соединены отрезками. При этом направление дуг сохраняется.
Граф называется простым, если он не содержит петель и параллельных дуг (ребер).
Путем в орграфе называется последовательность дуг, в которой конец каждой предыдущей дуги совпадает с началом следующей.
Циклом называется путь, у которого совпадают начальная и конечная вершины.
Для графов существует способ упорядочения (алгоритм Фалкерсона).
1)Находят вершины графа, в которые не входит ни одна дуга. Эти вершины образуют первую группу. Нумеруют вершины группы в натуральном порядке 1,2,… . При этом присвоение номеров внутри группы может быть произвольным.
2)Мысленно вычеркивают все пронумерованные вершины и дуги из них выходящие. В полученном графе находят вершины графа, в которые не входит ни одна дуга. Эти вершины образуют вторую группу. И т.д.
Аналогично можно упорядочивать по дугам.