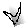Правила построения сетевых моделей
При построении сетевого графика необходимо следовать следующим правилам:
· длина стрелки не зависит от времени выполнения работы;
· стрелка может не быть прямолинейным отрезком;
· для действительных работ используются сплошные, а для фиктивных – пунктирные стрелки;
· каждая операция должна быть представлена только одной стрелкой;
· между одними и теми же событиями не должно быть параллельных работ, т.е. работ с одинаковыми кодами;
· следует избегать пересечения стрелок;
· не должно быть стрелок, направленных справа налево;
· номер начального события должен быть меньше номера конечного события;
· не должно быть висячих событий (т.е. не имеющих предшествующих событий), кроме исходного;
· не должно быть тупиковых событий (т.е. не имеющих последующих событий), кроме завершающего;
· не должно быть циклов (рис.1.2).
Рис.1.2. Недопустимость циклов
Исходные данные для построения сетевой модели могут задаваться различными способами, например,
· описанием предполагаемого проекта. В этом случае необходимо самостоятельно разбить его на отдельные работы и установить их взаимные связи;
· списком работ проекта. В этом случае необходимо проанализировать содержание работ и установить существующие между ними связи;
· списком работ проекта с указанием их упорядочения. В этом случае необходимо только отобразить работы на сетевом графике.
Построение сетевого графика необходимо начинать с выявления исходных работ модели. Если согласно условию некоторая работа может выполняться, не ожидая окончания каких-либо других работ, то такая работа является исходной в сетевой модели и ее начальным событием является исходное событие. Если исходных работ несколько, то их стрелки выходят все из одного исходного события.
Если, согласно условию, после окончания некоторой работы не должны выполняться никакие другие работы, то такая работа является завершающей работой сетевой модели и ее конечным событием является завершающее событие. Если завершающих исходных работ несколько, то их стрелки заходят все в одно завершающее событие.
Если, согласно условию, несколько работ имеют общее начальное и общее конечное события, то они являются параллельными, имеют одинаковый код, что недопустимо. Для устранения параллельности работ вводят дополнительное событие и фиктивную работу (которой в реальности не соответствует никакое действие) таким образом, чтобы конечные события работ различались (рис.1.3.).
Рис.1.3. Устранение параллельности двух работ
Постройте сетевую модель программы опроса общественного мнения, которая включает разработку (A; 1 день) и распечатку анкет (B; 0,5 дня), прием на работу (C; 2 дня) и обучение (D; 2 дня) персонала, выбор опрашиваемых лиц (E; 2 дня), рассылку им анкет (F; 1 день) и анализ полученных данных (G; 5 дней).
Из условия задачи нам известно содержание работ, но явно не указаны взаимосвязи между работами. Поэтому для их установления необходимо проанализировать смысл каждой конкретной работы и выяснить, какие из остальных работ должны ей непосредственно предшествовать. Исходной работой, начинающей сетевой график, в данном случае является «прием на работу» (С), поскольку все остальные работы должны выполняться уже принятыми на работу сотрудниками (рис.1.4). Перед выполнением всех работ по опросу общественного мнения сотрудников необходимо обучить персонал (D). Перед тем как разослать анкеты (F), их надо разработать (A), распечатать (B) и выбрать опрашиваемых лиц (E), причем работу с анкетами и выбор лиц можно выполнять одновременно. Завершающей работой проекта является анализ полученных данных (G), который нельзя выполнить без предварительной рассылки анкет (F). В результате этих рассуждений построим сетевую модель и пронумеруем события модели (см. рис.1.4).
Рис.1.4. Сетевая модель программы опроса общественного мнения
Постройте сетевую модель, включающую работы A, B, C. L, которая отображает следующее упорядочение работ:
1) A, B и C – исходные операции проекта;
5) E и H предшествуют I и J;
6) C, D, F и J предшествуют K;
В пункте 1) условия явно указано, что A, B и C являются исходными работами, поэтому изобразим их тремя стрелками, выходящими из исходного события 1. Пункт 2) условия означает, что стрелки работ A и B должны окончиться в одном событии, из которого выйдет стрелка работы D. Но поскольку стрелки работ A и B также и начинаются в одном событии, то имеет место параллельность работ, которая недопустима правилами построения сетевых моделей (см. рис.1.5).
Рис.1.5. Устранение параллельности работ A и B
Для ее устранения введем дополнительное событие 2, в которое войдет работа B, после чего соединим события 2 и 3, в которые входят работы A и B пунктирной стрелкой фиктивной работы. В данном случае фиктивная работа (2,3) не соответствует никакой реальной работе, а лишь отображает логическую связь между работами B и D. Дальнейшее построение рассмотрим с помощью рис.7.6
Рис.1.6. Сетевая модель задачи №1.2
Согласно пункту 3) условия задачи из события 2, выходят три стрелки работ E, F и H. Согласно пункту 4) условия задачи стрелки работ C и F должны войти в общее событие, из которого выйдет стрелка работы G. Проблема с параллельностью работ E и H [пункт 5) условия задачи] решается путем введения дополнительного события 5 и фиктивной работы (5,6). Для отображения в сетевой модели пункта 6) условия задачи введем стрелки работ D и J в событие 7, а связь работ F и C с работой K отобразим с помощью фиктивной работы (4,7). Стрелки работ F и C нельзя было напрямую вводить в событие 7, потому что после них должна следовать работа G, которая с работами D и J никак не связана. Стрелка работы L выходит из события 8, т.е. после окончания работы K в соответствии с пунктом 7) условия задачи.
Поскольку в условии не указано, что работы L, I и G предшествуют каким-либо другим работам, то эти работы являются завершающими и их стрелки войдут в завершающее событие 9. Нумерацию событий проводят после построения сетевого графика, следя за тем, чтобы номер начального события каждой работы был меньше номера ее конечного события.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
1. Элементы построения сетевых моделей
В основе метода сетевого планирования и управления (СПУ) лежит построение графика, по своему виду напоминающего сеть (переплетение нитей и узелков), поэтому график и получил название сетевого.
Сетевой моделью называется отображение процессов, выполнение которых подчинено достижению одной или нескольких целей, с указанием взаимосвязей между этими процессами.
Сетевым графиком называется график производства работ с установленными расчётом сроками их выполнения. Сетевой график представляет собой графическое изображение сетевой модели с рассчитанными параметрами.
Элементами сетевой модели являются работа, событие и путь:
а) работа – это трудовой процесс, требующий затрат времени и ресурсов.
Название работы является минимальной информацией о работе, содержащейся в сетевой модели (например, отрывка котлована, возведение каркаса, устройство кровли, поставка оборудования и т.д.).
Работа на графике изображается сплошной стрелкой, направленной слева направо с указанием над стрелкой продолжительности работы.
Работа, которая требует лишь затрат времени, называется работа – ожидание. Ожидание на графике изображается пунктирной стрелкой с указанием над стрелкой её продолжительности (например, процесс твердения бетона или ожидание поставки материалов). Эти работы требуют только затрат времени.
Для отображения правильной технологической последовательности между работами применяется зависимость. Ни времени, ни ресурсов «зависимость» не требует. На графике зависимость изображают пунктирной стрелкой, продолжительность которой равна нулю. В литературных источниках зависимость называют фиктивной работой.
Итак, понятие «работа» может иметь три значения:
работа
работа – ожидание
зависимость
б) событие – это итог какой-нибудь деятельности (работы), происходящей мгновенно. Любая работа начинается и заканчивается событием.
Событие не потребляет ни времени, ни трудовых ресурсов, оно обозначает только факт начала и окончания одной или нескольких работ. Событие графически обозначается кружком, внутри которого ставится его номер, или может обозначаться буквами.
Событие, не имеющее непосредственно предшествующих работ, называется исходным, не имеющее непосредственно следующих работ – завершающим. Событие, не являющееся ни исходным, ни завершающим, называется промежуточным.
На рис. 1 событие 1 – исходное, событие 6 – завершающее, события 2, 3, 4, 5 – промежуточные.
Все работы комплекса по отношению друг к другу подразделяются на данную, предшест-вующую и последующую работы. Обозначение работ см. на рис. 2.
в) путь – это непрерывная технологическая последовательность работ от исходного события к завершающему.
На рис. 3 дан сетевой график из восьми работ, одной зависимости и шести событий. На графике можно выделить 7 путей:
1-й путь проходит по событиям 1, 2, 3, 4, 6;
2-й путь проходит по событиям 1, 3, 5, 6;
3-й путь проходит по событиям 1, 2, 4, 6;
4-й путь проходит по событиям 1, 2, 3, 5, 6;
5-й путь проходит по событиям 1, 2, 3, 4, 5, 6;
6-й путь проходит по событиям 1, 2, 4, 5, 6;
7-й путь проходит по событиям 1, 3, 4, 5, 6.
Зная продолжительность каждой работы tij , можно определить продолжительность любого пути сетевого графика.
Продолжительность пути определяется как сумма продолжительностей работ, составляющих этот путь:
Критический путь – это путь, имеющий максимальную продолжительность. Он определяет конечный срок строительства, это самый трудоемкий и неблагоприятный путь.
Подкритический путь – это путь, продолжительность которого близка к продолжительности критического пути.
На рис. 3 длина различных путей от исходного события до завершающего равна:
1-й путь Т1 = 5 + 10 + 14 + 9 = 38;
4-й путь Т4 = 5 + 10 + 2 + 3 = 20;
5-й путь Т5 = 5 + 10 + 0 + 3 = 32;
6-й путь Т6 = 5 + 7 + 0 + 3 = 15;
7-й путь Т7 = 12 + 14 + 0 + 3 = 29.
Первый путь имеет наибольшую продолжительность из всех путей, значит, он является критическим.
Критическим путь назван потому, что, во-первых, из всех путей сетевого графика только он определяет общую продолжительность строительства; во-вторых, он указывает на работы, которые являются ведущими для выполнения заданного комплекса работ. Работы, лежащие на критическом пути, называются критическими.
На рис. 3 критическими работами являются 1-2; 2-3; 3-4; 4-6.
На сетевом графике критический путь выделяют красной двойной или жирной линией.
В сетевом графике может быть несколько критических путей одинаковой продолжительности. Определение продолжительности (длины) критического пути и критических работ – одна из основных задач, решаемых в методе сетевого планирования и управления (СПУ).
2. Правила построения сетевых моделей
В сетевой модели должна отражаться технологическая последовательность и очерёдность отдельных работ. Модель должна иметь простую форму. Стрелки должны быть направлены слева направо от события с меньшим номером к событию с большим номером, необходимо стремиться к минимальному пересечению отдельных работ.
2.1. Основные правила
1. Правило составных работ – любая работа а может быть разбита на составляющие, если после частичного выполнения её можно начать следующую работу б. При этом вводятся логические зависимости и дополнительные события (рис. 4).
2. Правило параллельных работ – если между двумя событиями необходимо показать две или несколько работ, которые выполняются параллельно, в модели вводятся дополнительное событие по окончании одной из параллельных работ и логическая зависимость (фиктивная работа) между ними (рис. 5).
3. Правило зависимых и независимых работ – если для начала одной работыг необходимо выполнение всех пред-шествующих работ a и б, а для начала работы в необходимо выполнение только работы a, то вводятся дополнительное событие и логическая зависимость (рис. 6).
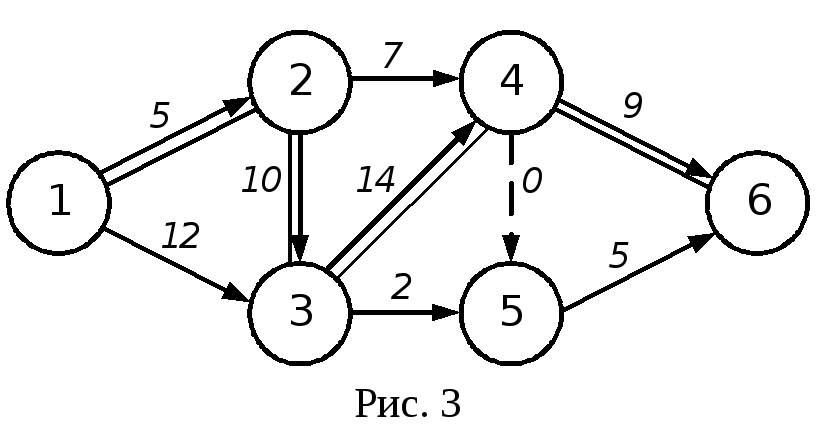
4. Правило запрещения замкнутых контуров, т.е. один путь не должен дважды проходить через одно событие (рис. 7).
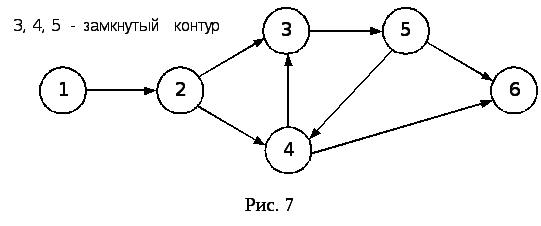
5. Правило запрещения тупиковых событий, т.е. событий, из которых не выходит ни одна работа, если событие не завершающее (рис. 8).
6. Правило запрещения необеспеченных событий, т.е. со- бытий, в которые не входит ни одна работа, если событие не исходное (рис. 9).
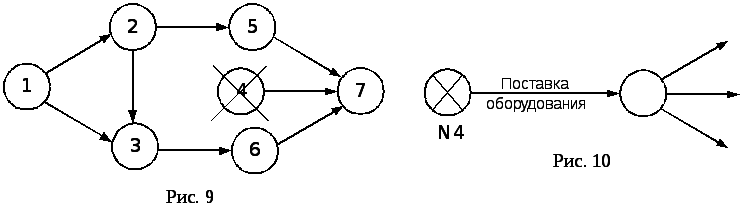
7. Правило изображения поставки (рис. 10).
2.2. Построение сетей
Для построения сетевой модели нужно знать технологию работ и зависимость одних работ от других. Последовательность выполнения работ записывается в форме таблицы, в которой указывается зависимость данной работы ig от предшествующей hi.
Пример 1. По данной зависимости работ построить сетевую модель.