Построение и виды сетевых работ моделей

15 Вопрос. Сущность и виды сетевых моделей.

Сетевая модель представляет собой описание комплекса работ (комплекса операций, проекта). Под ним понимается всякая задача, для выполнения которой необходимо осуществить достаточно большое количество разнообразных действий. Это может быть создание любого сложного объекта, разработка его проекта и процесс построения планов реализации проекта.

Сетевой график отражает операции проекта, которые необходимо выполнить, логическую последовательность и взаимозависимость этих операций и время начала и окончания самой продолжительной цепочки операций — критический путь.

Сетевой график раскрывает внутренние связи проекта и служит основой для календарного планирования работ и использования оборудования.

Сетевой график дает возможность оценить периоды времени, в течение которых выполнение операций может начинаться и заканчиваться, а также время допустимой задержки их выполнения.

Сетевой график позволяет определить, какие операции являются «критическими» и, следовательно, должны выполняться строго по графику, чтобы проект был завершен в запланированные сроки.

Виды сетевых моделей и графиков

По способу представления информации существуют два принципиально различных вида сетевых моделей (графиков):

1. Сетевой график типа «операции в узлах (ОУ)». Метод составления сетевых диаграмм, в которых плановые операции представляются прямоугольниками (или узлами). Плановые операции графически связаны одной или несколькими логическими взаимосвязями, которые показывают последовательность выполнения операций.

2. Сетевой график типа «операции на стрелках (ОС)». Метод построения сетевой диаграммы расписания, когда плановые операции отображаются на стрелках. Начало стрелки соответствует старту плановой операции, а конец – завершению (длина стрелки не отображает ожидаемую длительность плановой операции). Операции соединяются в точках, называемых узлами (обычно отображаются кружочками), для иллюстрации порядка, в котором операции могут исполняться

16Вопрос. Построение сетевых графиков типа «операции в узлах (оу)».

Метод составления сетевых диаграмм, в которых плановые операции представляются прямоугольниками (или узлами). Плановые операции графически связаны одной или несколькими логическими взаимосвязями, которые показывают последовательность выполнения операций.

В этом методе существует четыре типа зависимостей (или отношений предшествования):

• Финиш-старт. Инициация последующей операции зависит от завершения предшествующей операции.
• Финиш-финиш. Завершение последующей операции зависит от завершения предшествующей операции.
• Старт-старт. Инициация последующей операции зависит от инициации предшествующей операции.
• Старт-финиш. Завершение последующей операции зависит от инициации предшествующей операции.

В методе предшествования чаще всего используется отношение предшествования типа «финиш-старт». Отношения «старт-финиш» используются редко.

17 Вопрос. Построение сетевых графиков типа «операции на стрелках (ос)».

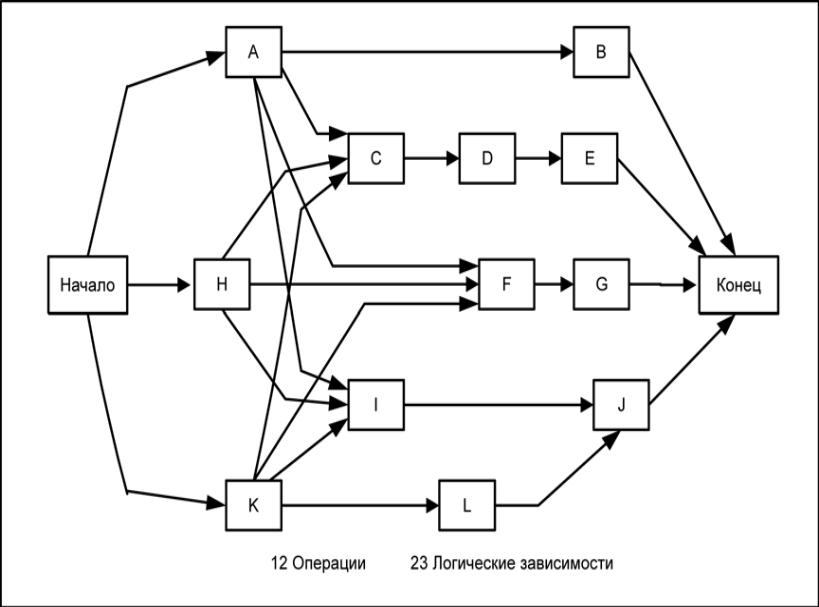
Метод стрелочных диаграмм – это метод построения сетевых диаграмм расписания проекта, в котором операции представляются в виде дуг, которые соединяются в узлах, показывающих их зависимости. На рис. 6-6 показана простая логическая сетевая диаграмма, построенная при помощи метода стрелочных диаграмм. Этот метод еще называется «операции на дугах»; несмотря на то что он реже используется, чем метод предшествования, он до сих пор используется в преподавании теории сетевых расписаний, а также в некоторых отдельных областях приложения.

В методе стрелочных диаграмм используются только зависимости «финиш-старт»; иногда для правильного отображения всех логических взаимосвязей проекта приходится прибегать к «фиктивным» отношениям, которые называются фиктивными операциями (на рисунке показаны пунктиром). Поскольку фиктивные операции не являются действительными плановыми операциями (в них нет содержания работ), им в целях анализа сети расписания присваивается нулевая длительность. К примеру, на рис. 6-6 плановая операция «F» зависит от завершения плановых операций «A» и «K» помимо завершения плановой операции «H».

Источник

3.4. Сетевые модели: общий вид, область применения,

В основе сетевого метода (СПУ – сетевое планирование и управление) лежит разработанная в 1958 г. в США система PERT – «техника обзора и оценки программ» или «Метод критического пути». В БССР сетевые методы стали широко применяться с 1962 г. Сетевые методы моделирования при решении вопросов организации строительства обеспечивают возможность учета практически всех особенностей строительного производства, что в свою очередь позволяет строительным организациям повысить эффективность строительства.

Общий вид сетевых моделей приведен на рисунках 3.3, 3.4..

Достонства сетевых методов заключаются в следующем:

– абсолютно достоверно через систему событий и технологических зависимостей можно видеть принятую взаимозависимость работ;

– можно выявить критические и некритические работы, и соответственно найти критический путь, как наибольший, характеризующий продолжительность строительства;

– по некритическим работам можно рассчитать возможные резервы (запасы) времени и исспользовать их в необходимых случаях.

Элементы сетевых моделей (графиков).

Сетевая модель изображается в виде системы, состоящеей из стрелок и кружков.

В основе построения сети лежат понятия «работа», «событие», «зависимость», «ожидание».

Работа – это производственные процесс, требующий затрат времени и материальных ресурсов и приводящий к достижению определенных результатов (например, рытье котлована, устройство фундаментов, монтаж конструкций). Работу изображают одной сплошной стрелкой длина которой может быть не связана с продолжительностью работы (если график составлен не в масштабе времени).

Как правило, над стрелкой указывают наименование работы, а под стрелкой – продолжительность работы в рабочих днях и при необходимости количество рабочих в день или смену. Под стрелкой можно показать также сметную стоимость СМР (тыс. руб.), физический объем работ, исполнителя работ и т.д. В некоторых материалах рекомендуют под стрелкой указывают наименование работы, а над стрелкой – продолжительность работы в рабочих днях и при необходимости количество рабочих в день или смену. В зависимости от назначения графика содержание приводимых параметров работы может меняться, но продолжительность и наименование работ указывают всегда.

Событие – это факт окончания одной или нескольких работ, необходимых и достаточных для начала следующих работ. В любой сетевой модели события устанавливают технологическую и организационную последовательность работ. События изображаются кружками или другими геометрическими фигурами, внутри которых (или рядом) указывается определенный номер – код события. События ограничивают рассматриваемую работу и по отношению к ней могут быть начальными и конечными.

Начальное событие определяет начало данной работы и является конечным для предшествующих работ. Конечное событие определяет окончание данной работы и является начальным для последующих работ.

Исходное событие – событие, которое не имеет предшествующих работ в рамках рассматриваемого сетевого графика. Завершающее событие – событие, которое не имеет последующих работ в рамках рассматриваемого сетевого графика (рис. 3.3, 3.4).

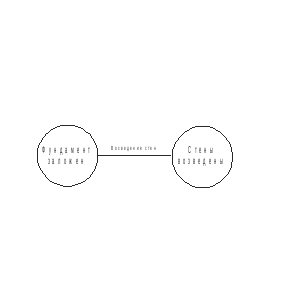
Рис. 3.3 Укрупненная сетевая модель возведения здания в одну захватку

Источник

1. Сетевая модель и ее основные элементы.

Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ (операций), заданного в специфической форме сети, графическое изображение которой называется сетевым графиком. Отличительной особенностью сетевой модели является четкое определение всех временных взаимосвязей предстоящих работ.

Главными элементами сетевой модели являются событиями и работы

Термин работа используется в СПУ в широком смысле.Во-первых, это действительная работа — протяженный во временипроцесс, требующий затрат ресурсов (например, сборка изделия, испытание прибора и т.п.). Каждая действительная работа, должна быть конкретной, четко описанной и иметь ответст­венного исполнителя.

Во-вторых, это ожидание — протяженный во времени процесс,не требующий затрат труда (например, процесс сушки после окраски, старения металла, твердения бетона и т.п.).

В-третьих, это зависимость, или фиктивная работа — логическая связь между двумя или несколькими работами (события), не требующими затрат труда, материальных ресурсов или времени. Она указывает, что возможность одной работы непосредственно зависит от результатов другой. Естественно, что продолжительность фиктивной работы принимается равной нулю.

Событие — это момент завершения какого-либо процесса, отражающий отдельный этап выполнения проекта. Событие может являться частным результатом отдельной работы или суммарным результатом нескольких работ. Событие может свершиться только тогда, когда закончатся все работы, ему предшествующие. Последующие работы могут начаться только тогда, когда событие свершится. Отсюда двойственный характер события: для всех непо­средственно предшествующих ему работ оно является конечным, а для всех непосредст­венно следующих за ним — начальным. При этом предполагается, что событие не имеет продолжительности и свершается как бы мгновенно. Поэтому каждое событие, включаемое в сетевую модель, должно быть полно, точно и всесторонне определено, его формулировка должна включать в себя результат всех непосредственно предшествующих ему работ.

Среди событий сетевой модели выделяют исходное и завершающее события. Исходное собы­тие не имеет предшествующих работ и событий, относящихся к представленному в модели комплексу работ. Завершающее событие не имеет последующих работ и событий.

События на сетевом графике (или, как еще говорят, на графе)изображаются кружками (вершинами графа), а работы — стрелками(ориентированными дугами), показывающими связь между работами. Пример фрагмента сетевого графика представлен на рис 1:

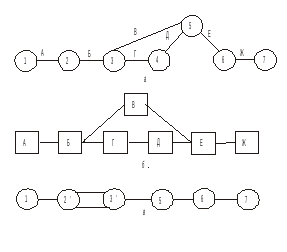
На рис. 2, а приведен сетевой график задачи моделирования и построения оптималь­ного плана некоторого экономического объекта. Чтобы решить эту задачу, необходимо провести следующие работы: А – сформулировать проблему исследования; В5 — матема­тическую модель изучаемого объекта; В — собрать информацию; Г — выбрать метод решения задачи; Д — построить и отладить программу для ЭВМ; Е — рассчитать опти­мальный план; Ж — передать результаты расчета заказчику. Цифрами на графике обозначены номера событий, к которым приводит выполнение соответствующих работ.

Из графика, например, следует, что работы В и Г можно начать выполнять независимо одна от другой только после свершения события 3, т.е. когда выполнены работы А и Б; работу Д — после свершения события 4, когда выполнены работы А, Б и Г; а работу Е можно выполнить только после наступления события 5, т.е. при выполнении всех предшествующих ему работ А, Б, В, Г и Д.

В сетевой модели, представленной на рис. 2 а, нет числовых оценок. Такая сеть называется структурной. Однако на практике чаще всего используются сети, в которых заданы оценки про­должительности работ (указываемые в часах, неделях, декадах, месяцах и т.д. над соответствую­щими стрелками), а также оценки других параметров, например трудоемкости, стоимости и т.п. Именно такие сети мы будем рассматривать в дальнейшем.

Но прежде сделаем следующее замечание. В рассмотренных примерах сетевые графики со­стояли из работ и событий. Однако может быть и иной принцип построения сетей — без событий. В такой сети вершины графа (например, изображенные прямоугольниками) означают определен­ные работы, а стрелки — зависимости между этими работами, определяющие порядок их выполнения. В качестве примера сетевой график «события — работы» задачи моделирования и построе­ния оптимального плана некоторого экономического объекта, приведенный на рис. 2 а, пред­ставлен в виде сети «работы — связи» на рис. 2 б. А сетевой график «события — работы» той же задачи, но с неудачно составленным перечнем работ, представлен на рис. 2 в (см. правило 3 в разд. 3).

Следует отметить, что сетевой график «работы — связи» в отличие от графика «события — ра­боты» обладает известными преимуществами: не содержит фиктивных работ, имеет более про­стую технику построения и перестройки, включает только хорошо знакомое исполнителям понятие работы без менее привычного понятия события. Вместе с тем сети без событий оказываются значительно более громоздкими, так как событий обычно значительно меньше, чем работ (пока­затель сложности сети, равный отношению числа работ к числу событий, как правило, существенно больше единицы). Поэтому эти сети менее эффективны с точки зрения управления ком­плексом. Этим и объясняется тот факт, что (при отсутствии в целом принципиальных различий между двумя формами пред­ставления сети) в настоящее время наибольшее распространение получили сетевые графики «со­бытия — работы».

Источник