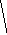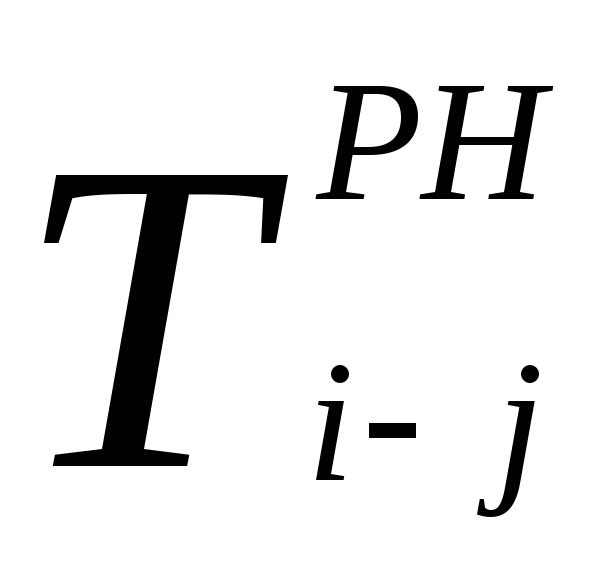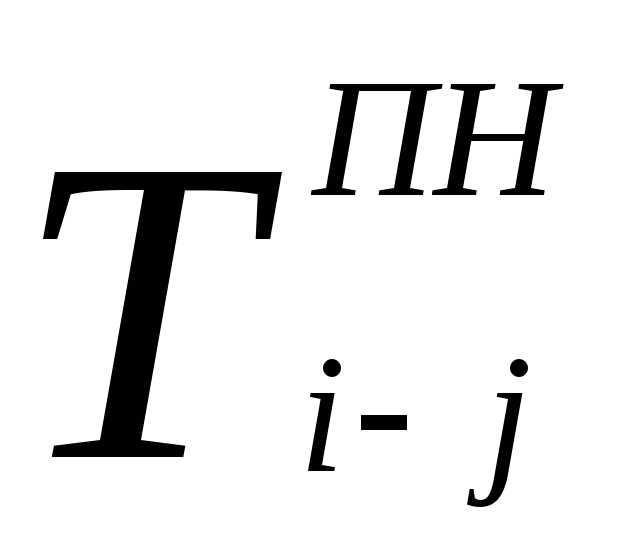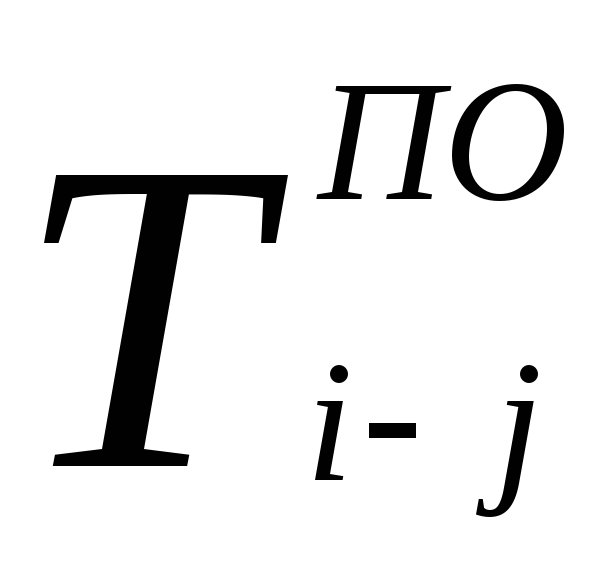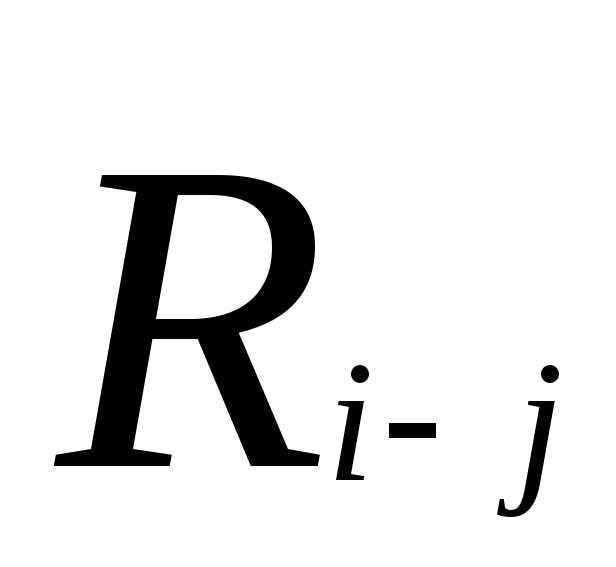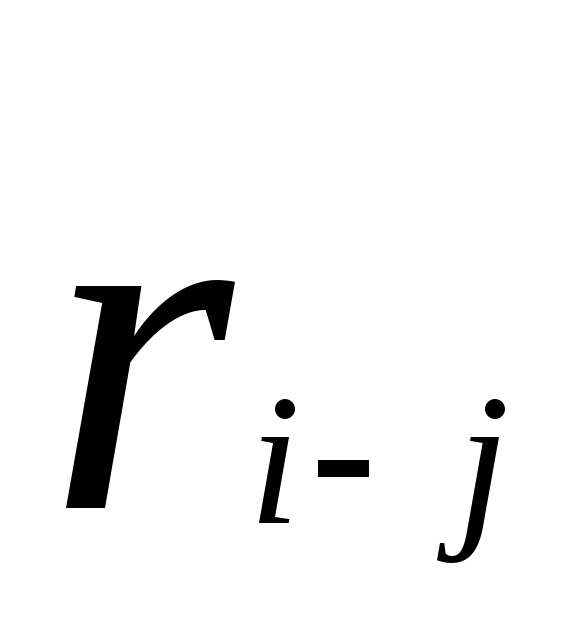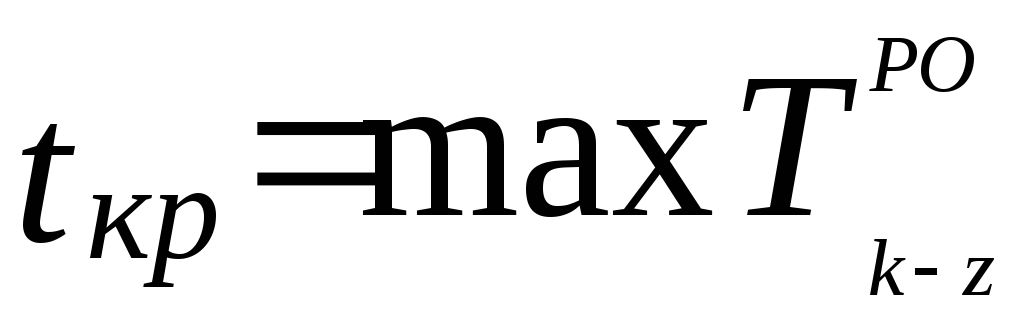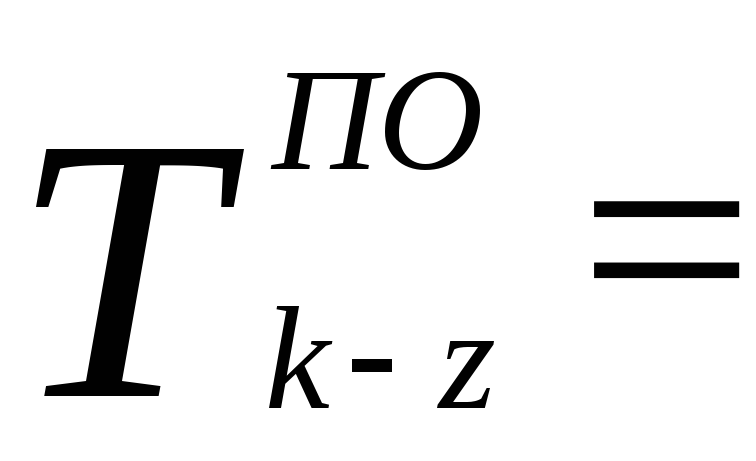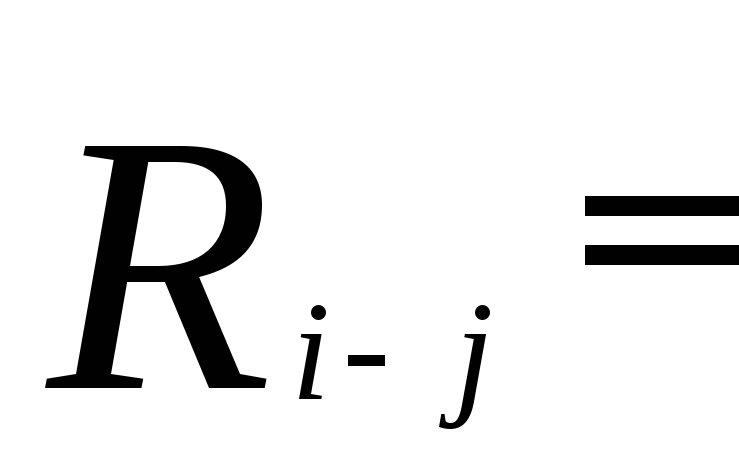Построение сетевой модели на примере

1.3.5. Пример построения и расчета сетевой модели

Исходные данные варианта лабораторной работы включают название и продолжительность каждой работы (табл. 1.1), а также описание упорядочения работ.

1. Работы C, I, Gявляются исходными работами проекта, которые могут выполняться одновременно.
2. Работы E иAследуют за работойC.
3. Работа Hследует за работойI.
4. Работы D иJследуют за работойG.
5. Работа Bследует за работойE.
6. Работа Kследует за работамиAиD, но не может начаться прежде, чем не завершится работаH.
7. Работа Fследует за работойJ.

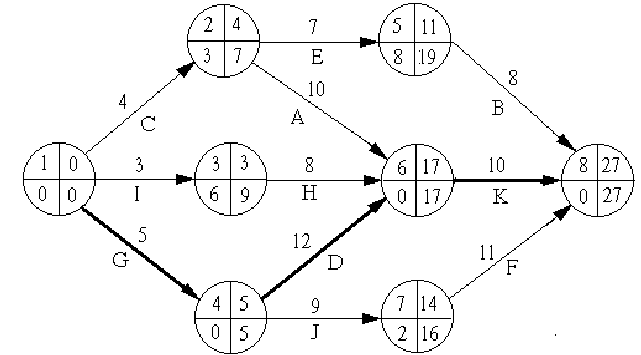
На рис.1.4 представлена сетевая модель, соответствующая данному упорядочению работ. Каждому событию присвоен номер, что позволяет в дальнейшем использовать не названия работ, а их коды (см. табл. 1.2). Численные значения временных параметров событий сети вписаны в соответствующие секторы вершин сетевого графика, а временные параметры работ сети представлены в табл. 1.3. Таблица 1.2 Описание сетевой модели с помощью кодирования работ

Номера событий		Код работы	Продолжительность
начального	конечного	работы
1	2	(1,2)	4
1	3	(1,3)	3
1	4	(1,4)	5
2	5	(2,5)	7
2	6	(2,6)	10
3	6	(3,6)	8
4	6	(4,6)	12
4	7	(4,7)	9
5	8	(5,8)	8
6	8	(6,8)	10
7	8	(7,8)	11

Рис.1.4. Сетевая модель Таблица 1.3 Временные параметры работ

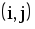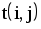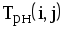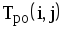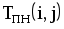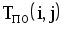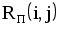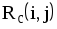1,2	4	0	4	3	7	3	0
1,3	3	0	3	6	9	6	0
1,4	5	0	5	0	5	0	0
2,5	7	4	11	12	19	8	0
2,6	10	4	14	7	17	3	3
3,6	8	3	11	9	17	6	6
4,6	12	5	17	5	17	0	0
4,7	9	5	14	7	16	2	0
5,8	8	11	19	19	27	8	8
6,8	10	17	27	17	27	0	0
7,8	11	14	25	16	27	2	2

1.4. Контрольные вопросы

1.4.1. Зачетный минимум

1. Определение события, виды событий, практические примеры событий, обозначение событий на графике, временные параметры событий.
2. Определение работы, классификация работ с приведением соответствующих практических примеров, обозначение работ на графике, временные параметры работ.
3. Правила построения сетевых графиков.
4. Определение пути в сетевом графике, виды путей, важность определения критического пути.
5. Умение вычислять временные параметры событий и работ.

1.4.2. Дополнительные вопросы

1. Почему при расчете раннего срока свершения события iвыбираютмаксимальнуюиз сумм ?
2. Почему при расчете позднего срока свершения события iвыбираютминимальнуюиз разностей ?
3. Какова взаимосвязь полного и свободного резервов работы?
4. Как можно найти критических путь в сетевой модели, без непосредственного суммирования длительностей работ?

Часть 2. ОПТИМИЗАЦИЯ СЕТЕВЫХ МОДЕЛЕЙ ПО КРИТЕРИЮ «МИНИМУМ ИСПОЛНИТЕЛЕЙ» 2.1. ЦЕЛЬ РАБОТЫ Знакомство с методикой и приобретение навыков проведения оптимизации сетевых моделей по критерию «Минимум исполнителей». 2.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Согласно номеру своего варианта получите данные о количество исполнителей, занятых на каждой работе сетевой модели, и ограничение по численности Nодновременно занятых в работе исполнителей. 2. Постройте в отчете графики привязки и загрузки, используя нормальные длительности работ сети — 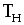(см. п.2.3.1), и покажите их преподавателю. 3. Проверьте правильность построения графиков привязки и загрузки с помощью компьютера, в случае необходимости выявите и устраните ошибки. 4. Используя компьютерную программу, проведите уменьшение численности исполнителей, одновременно занятых на работах сети, до требуемого уровня N. 5. Отчет по лабораторной работе должен содержать:

• номер варианта;
• исходные данные варианта;
• графики привязки и загрузки до проведения оптимизации загрузки;
• графики привязки и загрузки после проведения оптимизации загрузки (возможно использование пунктирных линий на первоначально построенных графиках для отображение изменений в привязке работ и загрузке сети, вызванных сдвигами работ);
• коды работ, сдвинутых в процессе оптимизации, и время их сдвига.

Источник

Пример построения сетевого графика

Используя полученные данные, мы можем найти основные характеристики сетевой модели табличным методом, критический путь и его продолжительность.
Таблица – Табличный метод расчета сетевого графика.

КПР	Код работы (i,j)	Продолжительность работы t(i, j)	Ранние сроки		Поздние сроки		Резервы времени
			tрн(i,j)	tро(i,j)	tпн(i,j)	tпо(i,j)	Rп	Rc
1	2	3	4	5	6	7	8	9
0	1,2	7	0	7	0	7	0	0
0	1,4	4	0	4	17	21	17	8
0	1,5	3	0	3	19	22	19	0
1	2,3	3	7	10	7	10	0	0
1	2,8	13	7	20	19	32	12	12
1	3,4	2	10	12	19	21	9	0
1	3,6	13	10	23	10	23	0	0
2	4,7	5	12	17	21	26	9	0
1	5,7	4	3	7	22	26	19	10
1	6,8	9	23	32	23	32	0	0
2	7,8	6	17	23	26	32	9	9

Таким образом, работы критического пути (1,2),(2,3),(3,6),(6,8). Продолжительность критического пути Т_кр=32.

Рисунок — Масштабный график сетевой модели
Для оценки вероятности выполнения всего комплекса работ за 30 дней нам необходима следующая формула: P(t_кр где Z=(Т-Т_кр)/S_кр
Z- нормативное отклонение случайной величины, S_кр – среднеквадратическое отклонение, вычисляемое как корень квадратный из дисперсии продолжительности критического пути. Соответствие между Z и Ф(Z) представлено в таблице.
Таблица — Таблица стандартного нормального распределения.

Z	F(Z)	Z	F(Z)	Z	F(Z)
0	0.0000	1.0	0.6827	2.0	0.9643
0.1	0.0797	1.1	0.7287	2.1	0.9722
0.2	0.1585	1.2	0.7699	2.2	0.9786
0.3	0.2358	1.3	0.8064	2.3	0.9836
0.4	0.3108	1.4	0.8385	2.4	0.9876
0.5	0.3829	1.5	0.8664	2.5	0.9907
0.6	0.4515	1.6	0.8904	2.6	0.9931
0.7	0.5161	1.7	0.9104	2.7	0.9949
0.8	0.5763	1.8	0.9281	2.8	0.9963
0.9	0.6319	1.9	0.9545	2.9	0.9973

Критический путь проходит по работам (1,2)(2,3)(3,6)(3,8).
Дисперсия критического пути:
S 2 ­(L_кр)= S 2 (1,2)+ S 2 (2,3)+ S 2 (3,6)+S 2 (6,8)=1+0,25+4+1=6,25
S(L_кр)=2,5
p(t_кр<30)=0,5+0,5Ф((30-32)/2,5)=0,5-0,5Ф(0,8) = 0,5-0,5*0,5763=0,5-0,28815=0,213
Вероятность того, что весь комплекс работ будет выполнен не более чем за 30 дней, составляет 21,3%.
Для определения максимально возможного срока выполнения всего комплекса работ с надежностью 95% будем использовать следующую формулу: T=Т_кр+Z*S_кр Для решения поставленной задачи найдем значение аргумента Z, которое соответствует заданной вероятности 95% (значению графы Ф(Z) 0,9545*100% в таблице 5 соответствует Z=1,9).
T=32+1,9*2,5=36,8
Максимальный срок выполнения всего комплекса работ при заданном уровне вероятности 95% составляет всего 36,8 дня.

Источник

1.4. Построение сетевой модели

Рассмотрим пример построения сетевой модели для объекта* с исходными данными, приведенными в табл. 1.

Т а б л и ц а 1 – Исходные данные для построения сетевой модели

Продолжительность работ, дн.

*Примечание. Объект одноэтажный, трехпролетный, промышленного назначения.

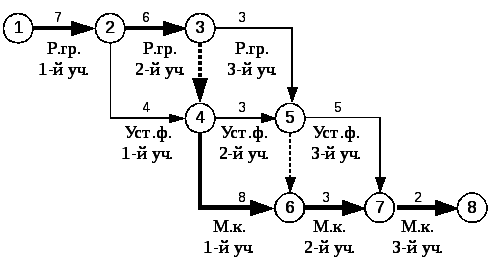
На рисунке 9 потоки однородных работ выделены чётко, однако критический путь (1-2, 2-3, 3-4, 4-6, 6-7, 7-8), равный 26 дням, является ложным, так как технологически работа 4-6 (монтаж конструкций на первом участке) не зависит от окончания работы 2-3 (разработка грунта на втором участке).

Рисунок 9 — График с нереальными зависимостями между работами:

Р. гр. – разработка грунта; Уст.ф. – усройство фундаментов; М.к. – монтаж конструкций

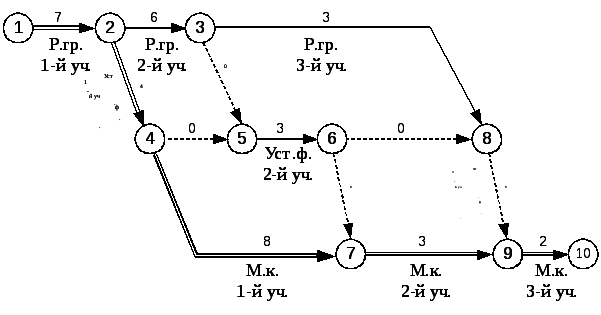
На рисунке 10 представлен правильно построенный сетевой график.

Рисунок 10 — График с реальными зависимостями между работами

Критический путь (1-2, 2-4, 4-7, 7- 9, 9-10) равен 24 дням.

Задание № 2 Расчёт сетевых графиков

2.1. Расчётные параметры сетевых графиков и расчётные формулы

Рисунок 11 — Схема сетевого графика

i-j – рассматриваемая работа;

h₁-i, h₂-i – предшествующие работы;

t_кр – продолжительность критического пути;

–раннее начало работы;

–раннее окончание работы;

–позднее начало работы;

–позднее окончание работы;

–общий резерв времени работы;

–частный резерв времени работы.

Раннее начало работы, самый ранний из возможных сроков начала работы, который определяется продолжительностью максимального пути от исходного события графика до начала данной работы. Работы, выходящие из одного события, имеют одинаковые ранние начала. Ранние начала работ, выходящих из начального события, равны нулю. Раннее начало любой работы равно наибольшему из ранних окончаний предшествующих работ.

= . (1)

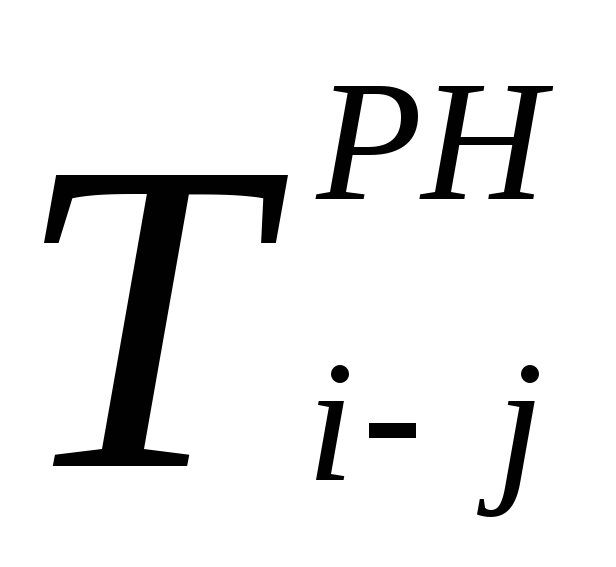
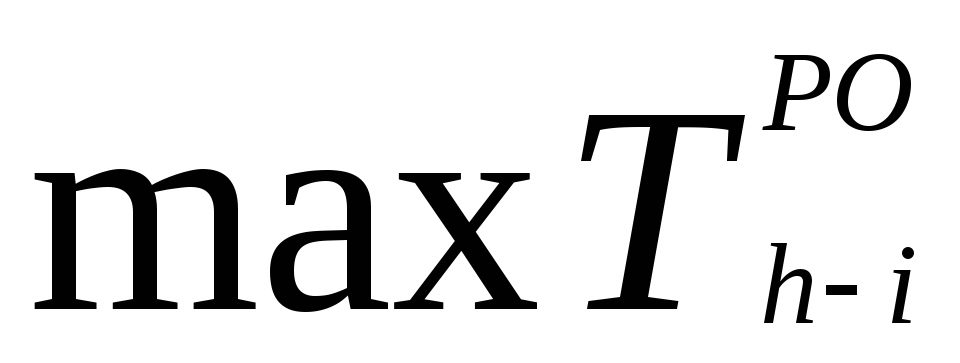
Раннее окончание работы – это самый ранний из возможных сроков окончания работы, оно равно сумме раннего начала работы и её продолжительности

=. (2)

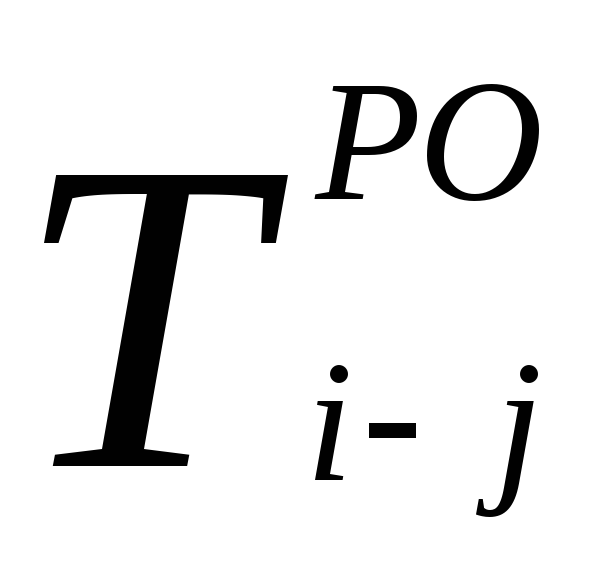
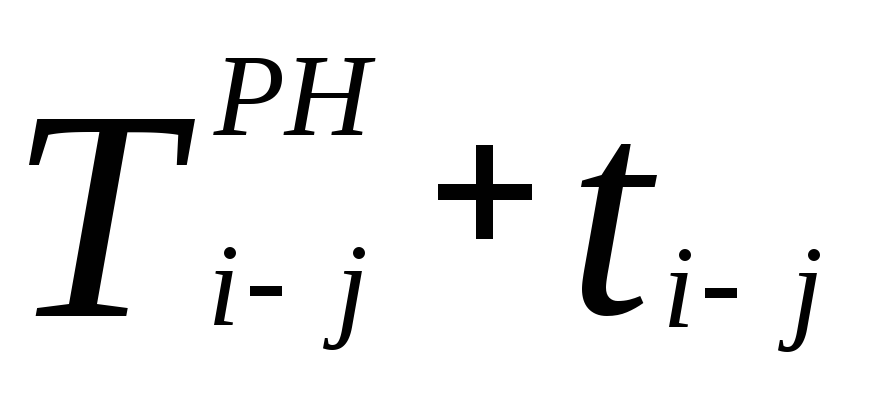
Максимальная величина из ранних окончаний работ, входящих в завершающее событие графика, определяет продолжительность критического пути и срок строительства

, (3)

где к-z – завершающая работа.

Позднее начало работы – самый поздний допустимый срок начала работы, при котором срок достижения конечной цели не меняется.

Позднее окончание работы – самый поздний допустимый срок окончания работы, не изменяющий конечной цели.

Позднее окончание определяется разностью между продолжительностью максимального пути от последующего события данной работы до завершающего события графика или равно наименьшему из поздних начал последующих работ

= =. (4)

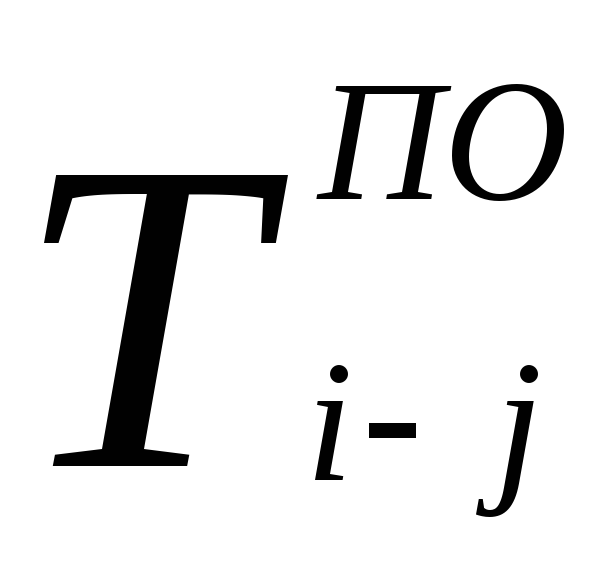
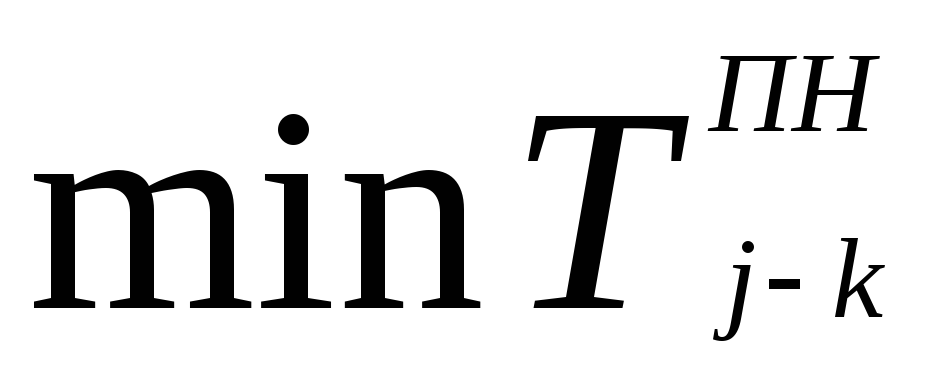
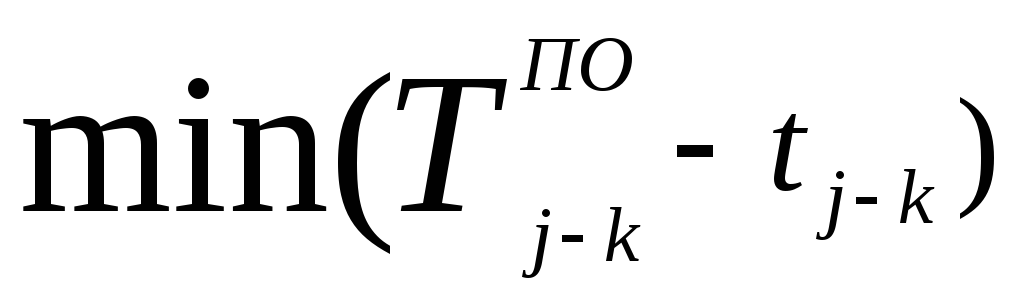
Позднее начало данной работы равно разности между величинами её позднего окончания и продолжительности

=. (5)

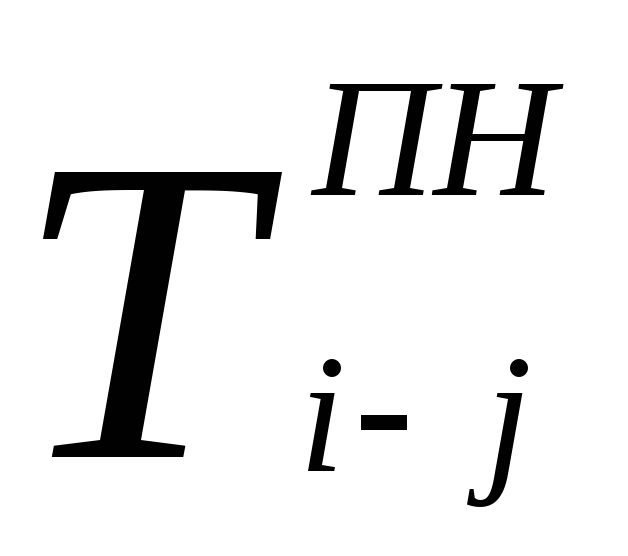
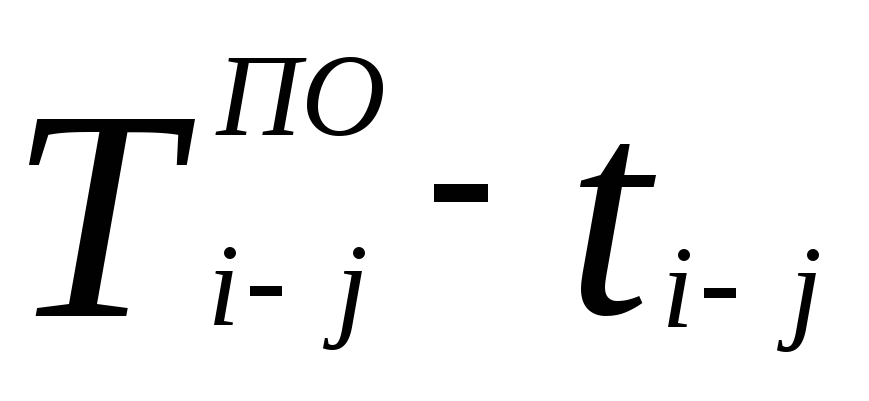
Для завершающих работ позднее окончание равно

. (6)

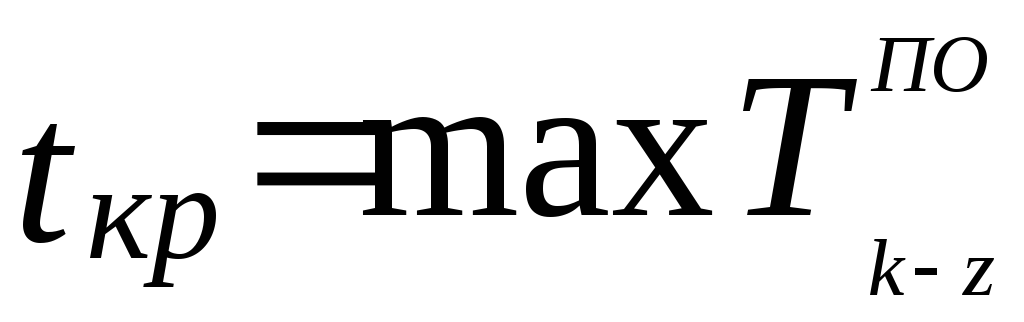
Общий резерв времени работы – это максимальное количество времени, на которое можно отдалить окончание данной работы за счёт увеличения продолжительности или задержки её начала, не изменяя срока достижения конечной цели.

Численно общий резерв времени работы определяется как разность между одноимёнными поздними и ранними параметрами этой работы

=— (7)

— . (8)

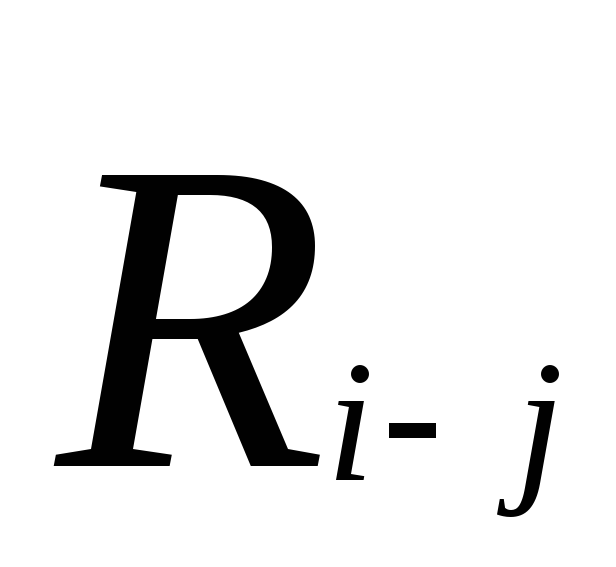
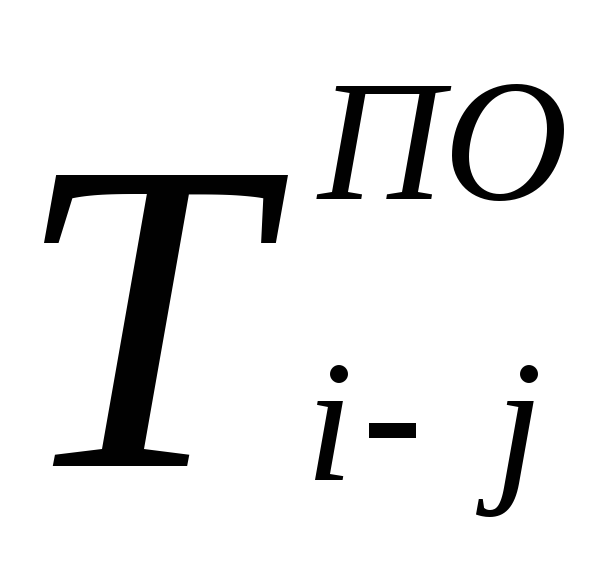
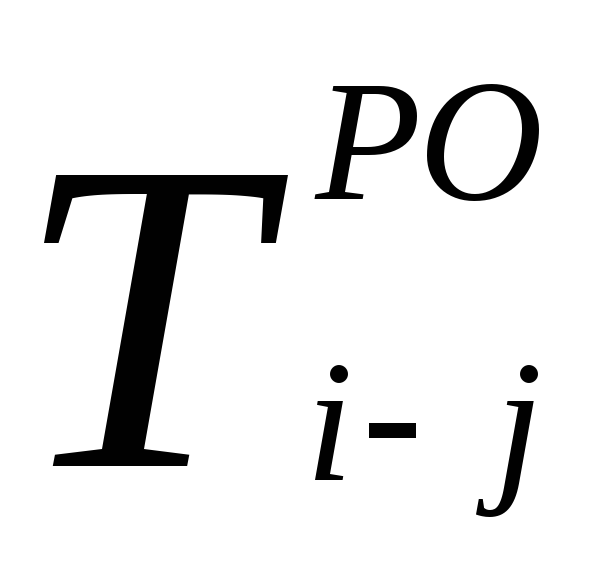
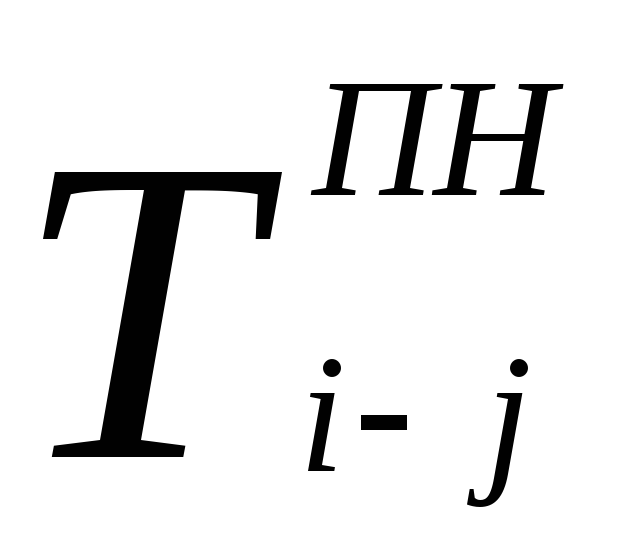
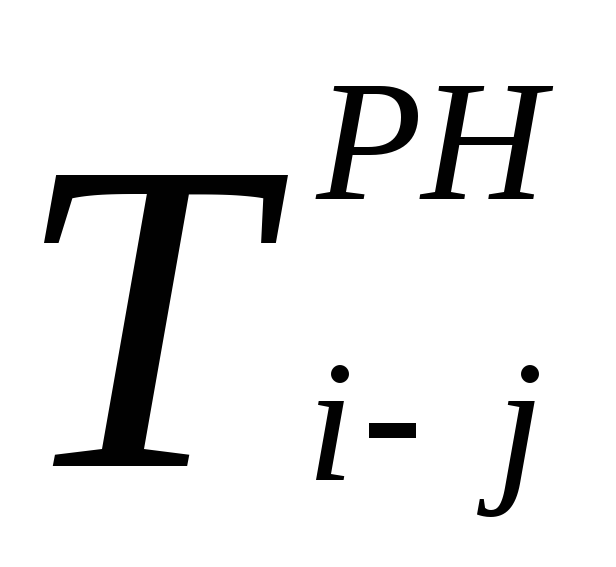
Частный резерв времени работы – это количество времени, на которое можно перенести начало работы или увеличить её продолжительность без изменения раннего начала последующих работ.

Численно частный резерв времени работы определяется как разность между ранним началом последующих работ и ранним окончанием данной работы.

=—. (9)

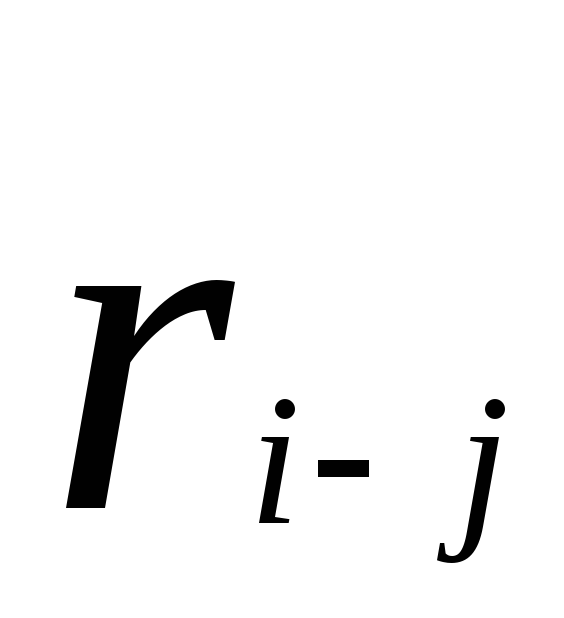
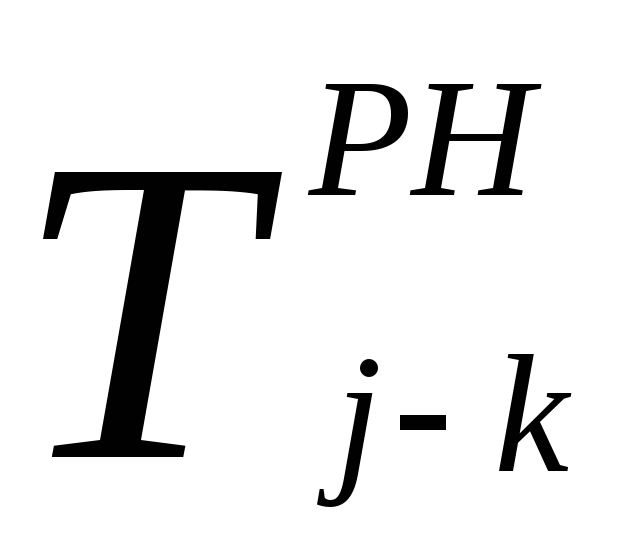
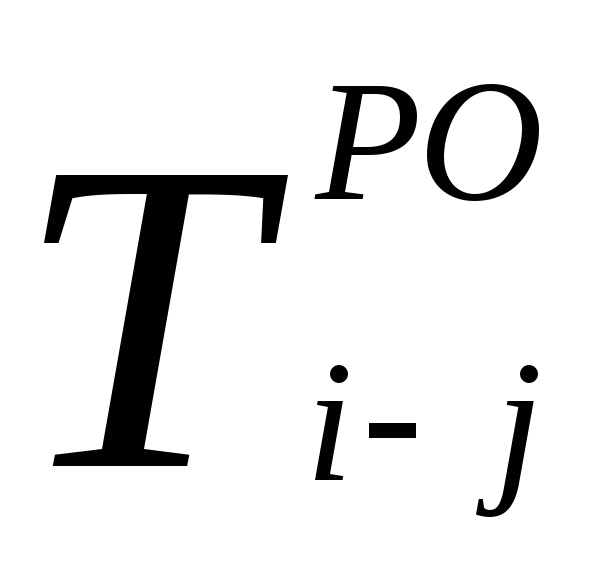
Расчёт модели сетевого графика сводится к определению расчётных параметров и критического пути.

Существуют ручные методы расчёта и на ЭВМ.

Из ручных методов расчёта наиболее распространены: табличный; непосредственно на графике; по потенциалам событий.

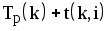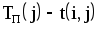Источник