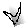1. Элементы построения сетевых моделей
В основе метода сетевого планирования и управления (СПУ) лежит построение графика, по своему виду напоминающего сеть (переплетение нитей и узелков), поэтому график и получил название сетевого.
Сетевой моделью называется отображение процессов, выполнение которых подчинено достижению одной или нескольких целей, с указанием взаимосвязей между этими процессами.
Сетевым графиком называется график производства работ с установленными расчётом сроками их выполнения. Сетевой график представляет собой графическое изображение сетевой модели с рассчитанными параметрами.
Элементами сетевой модели являются работа, событие и путь:
а) работа – это трудовой процесс, требующий затрат времени и ресурсов.
Название работы является минимальной информацией о работе, содержащейся в сетевой модели (например, отрывка котлована, возведение каркаса, устройство кровли, поставка оборудования и т.д.).
Работа на графике изображается сплошной стрелкой, направленной слева направо с указанием над стрелкой продолжительности работы.
Работа, которая требует лишь затрат времени, называется работа – ожидание. Ожидание на графике изображается пунктирной стрелкой с указанием над стрелкой её продолжительности (например, процесс твердения бетона или ожидание поставки материалов). Эти работы требуют только затрат времени.
Для отображения правильной технологической последовательности между работами применяется зависимость. Ни времени, ни ресурсов «зависимость» не требует. На графике зависимость изображают пунктирной стрелкой, продолжительность которой равна нулю. В литературных источниках зависимость называют фиктивной работой.
Итак, понятие «работа» может иметь три значения:
работа
работа – ожидание
зависимость
б) событие – это итог какой-нибудь деятельности (работы), происходящей мгновенно. Любая работа начинается и заканчивается событием.
Событие не потребляет ни времени, ни трудовых ресурсов, оно обозначает только факт начала и окончания одной или нескольких работ. Событие графически обозначается кружком, внутри которого ставится его номер, или может обозначаться буквами.
Событие, не имеющее непосредственно предшествующих работ, называется исходным, не имеющее непосредственно следующих работ – завершающим. Событие, не являющееся ни исходным, ни завершающим, называется промежуточным.
На рис. 1 событие 1 – исходное, событие 6 – завершающее, события 2, 3, 4, 5 – промежуточные.
Все работы комплекса по отношению друг к другу подразделяются на данную, предшест-вующую и последующую работы. Обозначение работ см. на рис. 2.
в) путь – это непрерывная технологическая последовательность работ от исходного события к завершающему.
На рис. 3 дан сетевой график из восьми работ, одной зависимости и шести событий. На графике можно выделить 7 путей:
1-й путь проходит по событиям 1, 2, 3, 4, 6;
2-й путь проходит по событиям 1, 3, 5, 6;
3-й путь проходит по событиям 1, 2, 4, 6;
4-й путь проходит по событиям 1, 2, 3, 5, 6;
5-й путь проходит по событиям 1, 2, 3, 4, 5, 6;
6-й путь проходит по событиям 1, 2, 4, 5, 6;
7-й путь проходит по событиям 1, 3, 4, 5, 6.
Зная продолжительность каждой работы tij , можно определить продолжительность любого пути сетевого графика.
Продолжительность пути определяется как сумма продолжительностей работ, составляющих этот путь:
Критический путь – это путь, имеющий максимальную продолжительность. Он определяет конечный срок строительства, это самый трудоемкий и неблагоприятный путь.
Подкритический путь – это путь, продолжительность которого близка к продолжительности критического пути.
На рис. 3 длина различных путей от исходного события до завершающего равна:
1-й путь Т1 = 5 + 10 + 14 + 9 = 38;
4-й путь Т4 = 5 + 10 + 2 + 3 = 20;
5-й путь Т5 = 5 + 10 + 0 + 3 = 32;
6-й путь Т6 = 5 + 7 + 0 + 3 = 15;
7-й путь Т7 = 12 + 14 + 0 + 3 = 29.
Первый путь имеет наибольшую продолжительность из всех путей, значит, он является критическим.
Критическим путь назван потому, что, во-первых, из всех путей сетевого графика только он определяет общую продолжительность строительства; во-вторых, он указывает на работы, которые являются ведущими для выполнения заданного комплекса работ. Работы, лежащие на критическом пути, называются критическими.
На рис. 3 критическими работами являются 1-2; 2-3; 3-4; 4-6.
На сетевом графике критический путь выделяют красной двойной или жирной линией.
В сетевом графике может быть несколько критических путей одинаковой продолжительности. Определение продолжительности (длины) критического пути и критических работ – одна из основных задач, решаемых в методе сетевого планирования и управления (СПУ).
Разработка тактики реализации проекта. Построение сетевых моделей.
Проект состоит из многих стадий и этапов, выполняемых различными исполнителями. Этот сложный процесс должен быть четко скоординирован и увязан во времени. К системам планирования и управления предъявляются следующие требования: способность оценить текущее состояние, предсказать дальнейший ход работ, помочь выбрать правильное направление для воздействия на текущие проблемы с тем, чтобы весь комплекс работ был выполнен в установленные сроки согласно бюджету. На данном этапе происходит определение последовательности выполнения работ, входящих в состав ИСР, результатом чего являются сетевой график. Этот график представляет информационно-динамическую модель, отражающую взаимосвязи между работами, необходимыми для достижения конечной цели проекта. В основе сетевого планирования лежит изображение планируемого комплекса работ в виде ориентированного графа, т.е. графической схемы, состоящей из точек — вершин графа, соединенных направленными линиями — стрелками, которые называются ребрами графа. Возможно два подхода к построению сетевых моделей. При первом — стрелками на графике изображаются работы, а вершинами — события. Такие модели относят к типу «Работа-стрелка» и называют сетевыми графиками.При втором подходе, наоборот, стрелкам соответствуют события, а вершинам — работы.Такие модели относят к типу «Работа-вершина» и называют сетями предшествования. На Рисунок 9 и 10 показаны примеры данных типов моделей.Рисунок 9 — Сетевая модель типа «Работа-стрелка» — Сетевой график. Рисунок 10. Сетевая модель типа «Работа-вершина» — Сеть предшествования. Работами (задачами) являются любые действия, приводящие к достижению определенных результатов — событий.События, кроме исходного, являются результатами выполнения работ. Между двумя смежными событиями может выполняться только одна работа или последовательность работ. Для построения сетевых моделей необходимо определить логические взаимосвязи между работами. Причиной взаимосвязей являются, как правило, технологические ограничения (начало одних работ зависит от завершения других). Комплекс взаимосвязей между работами определяет последовательность выполнения работ во времени. Связи предшествования (логические зависимости)—отображают природу зависимостей между работами.Большинство связей в проектах относятся к типу «конец-начало», когда последующая работа может начаться только по завершении предшествующей работы. Связи предшествования образуютструктуру сети. Комплекс взаимосвязей между работами часто также называют логической структурой проекта, поскольку он определяет последовательность выполнения работ. Для определения последовательности необходима следующая информация: перечень работ, описание продукта, технологические, дискретные и внешние взаимосвязи, ограничения и предположения.
Построение сетевых графиков:
В сетевом графике события обозначаются кружком с указанием номера внутри события, а работа стрелкой, последовательное начертание работ и событий и означает построение сетевого графика. Любая последовательность работ в сетевом графике, в котором конечное событие одной работы совпадает с начальным событием следующей за ней работы и т.д., называется путем. При выполнении следующих друг за другомработ каждая последующая работа может быть начата только после получения результатов всех предшествующих работ, т.е. после наступления определенных событий. После построения взаимосвязей для каждой работы экспертным путем определяется время ее выполнения, которое проставляется в сети над соответствующей стрелкой. Построение сетей предшествования:
- В сетях предшествования события обозначаются стрелкой, а работа блоком, форма которого может быть произвольной и зависит от используемых программных средств.
- Для описания зависимостей между работами в сетях предшествования может использоваться четыре типа связей, приведенных на Рисунок 11.
| Связь»Окончание-начало«- это стандартная последовательность, при которой предшествующая работа должна завершится до начала последующей. |  |
| Связь»Начало-начало«- это стандартная последовательность работ, при которой работы должны выполняться параллельно. В этом случае не требуется завершения предшествующей работы до начала последующей, для ее начала необходимо, чтобы предшествующая работа только началась. |  |
| Связь»Окончание-окончание«- в этом случае окончание последующей работы — 1 контролируется окончанием работы предшественницы — 2. В данном случае работы 1 и 2 должны закончится одновременно. |  |
| Связь»Начало-окончание«- этот тип связи означает, что работа 1 должна закончится до начала работы 2. Данный тип связи используется редко, но он может быть полезен, когда при планировании требуется задержать окончание работы на как можно более длительный срок, связав ее окончание с началом другой работы. |  |
Рисунок 11 — Типы связей в сетях предшествования. В современных программных продуктах управления проектами преимущественно используются сети предшествования, так их программная реализация более проста. В качестве примера можно привести один из видов сетей предшествования — диаграмму Ганта, применяемую во многих программных средствах и изображенную на Рисунок 16. 
Для продолжения скачивания необходимо пройти капчу:
2. Правила построения сетевых моделей
В сетевой модели должна отражаться технологическая последовательность и очерёдность отдельных работ. Модель должна иметь простую форму. Стрелки должны быть направлены слева направо от события с меньшим номером к событию с большим номером, необходимо стремиться к минимальному пересечению отдельных работ.
2.1. Основные правила
1. Правило составных работ – любая работа а может быть разбита на составляющие, если после частичного выполнения её можно начать следующую работу б. При этом вводятся логические зависимости и дополнительные события (рис. 4).
2. Правило параллельных работ – если между двумя событиями необходимо показать две или несколько работ, которые выполняются параллельно, в модели вводятся дополнительное событие по окончании одной из параллельных работ и логическая зависимость (фиктивная работа) между ними (рис. 5).
3. Правило зависимых и независимых работ – если для начала одной работыг необходимо выполнение всех пред-шествующих работ a и б, а для начала работы в необходимо выполнение только работы a, то вводятся дополнительное событие и логическая зависимость (рис. 6).
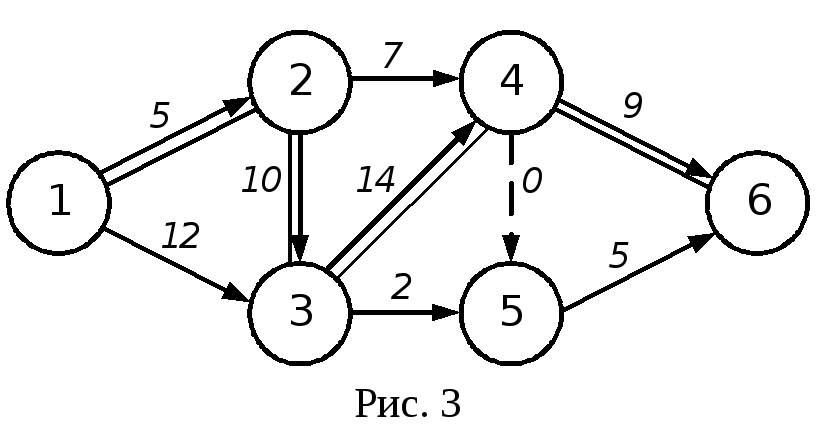
4. Правило запрещения замкнутых контуров, т.е. один путь не должен дважды проходить через одно событие (рис. 7).
5. Правило запрещения тупиковых событий, т.е. событий, из которых не выходит ни одна работа, если событие не завершающее (рис. 8).
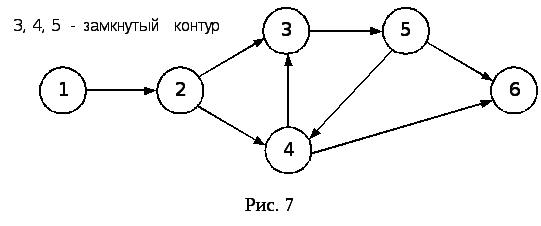
6. Правило запрещения необеспеченных событий, т.е. со- бытий, в которые не входит ни одна работа, если событие не исходное (рис. 9).
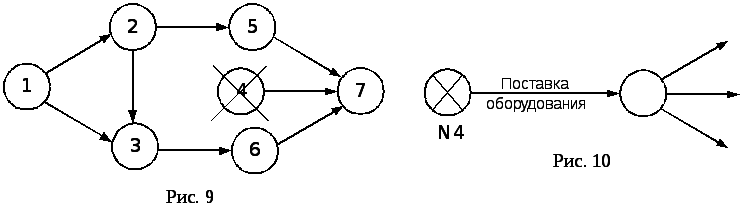
7. Правило изображения поставки (рис. 10).
2.2. Построение сетей
Для построения сетевой модели нужно знать технологию работ и зависимость одних работ от других. Последовательность выполнения работ записывается в форме таблицы, в которой указывается зависимость данной работы ig от предшествующей hi.
Пример 1. По данной зависимости работ построить сетевую модель.